同じ振動数,同じ波長( $v = f \,\lambda$ より,波の速さも同じ),そして振幅も同じ の2つの波が,
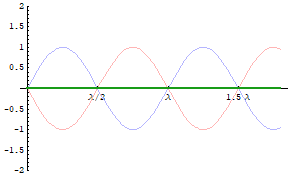
★互いに逆向きに進むとき,その合成波は定常波(下図の緑線)になります。定常波とは,見かけ上移動しないように見える波のことで,振幅(振動の大きさ)が位置の関数として場所ごとに決まっていて,空間的に周期性をもって(一定間隔で)変化しているとき,波は移動しないように見えるのです。
(注.2つの波の振動数,波長が同じでも振幅が違うと,合成波は移動するように見え,定常波にはなりません。)
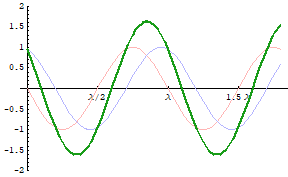
★2つの波が同じ向きに進むとき,その合成波は進行波(下図の緑線)になります。進行波とは,読んで字のごとく移動していくように見える波のことで,普通に見かける波と同じ動きをします。定常波の場合とは異なり各点はすべて同じ振幅で振動しますが,その振幅自体は2つの波の重なり具合,つまり位相差によって違ってきます。下図は2つの波の位相差が $2\pi/5$ の場合の例で,振幅は一つの波の振幅のおよそ $1.6$ 倍ぐらいになっています。
定常波についての詳細は,『2つの波の重ね合わせ・定常波』を参照してください。
◎平面波の反射による合成波:
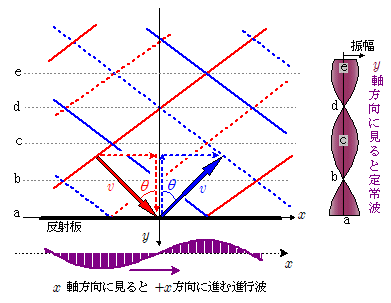
上図は, 振動数 $f$ ,波長 $\lambda$ (速さ $v = f\, \lambda$ )の平面波が $y$ 軸に対して角 $\theta$ の方向に入射し,反射板( $x$ 軸)で反射しているときの波線の様子を表します。赤(入射波),青(反射波)のそれぞれ実線が波の山を,破線が波の谷の線を表すとします。
このとき,入射波も反射波も $x$ 軸方向にはともに正方向に同じ速さで進んでいますので,合成波も $x$ 軸正方向に移動するように見えます。つまり進行波ができています。一方, $y$ 軸方向には入射波と反射波は互いに逆向きに進んでいることから, $y$ 軸方向に見たとき合成波は定常波になっているはずです。定常波というのは振幅が場所によって決まった波のことでしたから, $y$ 軸方向にみると反射板からの距離,この場合は $y$ 座標の値によって振幅が決まっている…ということになります。
上図において,反射板の位置a( $x$ 軸)や破線c,e,…の位置では,入射波と反射波の山どうし,あるいは谷どうしが重なっており,この線上には大きな波ができています。これに対し,破線b,d,…の線上では入射波と反射波の山と谷が重なっていて打ち消し合っており,すべての点で変位はゼロになっています。この状況は時間が経っても変わりません。つまりこの線上の点は,常に全く振動しないことになります。このことから,合成波を $y$ 軸方向に見たとき,振幅の大きいところと振幅ゼロのところが一定間隔で周期的に並んでいることが分かります。すなわち,a,c,e…では振幅最大の波の通り道であり定常波の『腹』に相当し,b,d,…では振幅がゼロの波の通り道で定常波の『節』に相当する…というわけです(振幅ゼロの点を結んだ線を『節線』という)。
以上より,合成波は全体として $x$ 軸正方向に移動するように見え,しかもその 振幅が $y$ 軸方向に周期的に変化している…ということになります。合成波の移動方向が,本来の波の入射方向でも反射方向でもない…という点が面白いですね。
シミュレーションにおいて,白いコブのようなものが $x$ 軸方向に移動していくように見えたのは,入射波と反射波の山どうしが重なった最も変位の大きい部分が移動していく様子が見えていたことになります。
上の例は波が『自由端反射』をしている場合の話です。『自由端反射』というのは,波が反射する際に,「山」の状態で入射した場合は「山」の状態で反射し,「谷」なら「谷」で反射する…というものです。
これに対して,反射の際に「山」と「谷」が反転した状態で反射する場合があります(「位相差πで反射する」と言う)。このような反射の仕方を『固定端反射』といい,振幅最大の位置とゼロの位置が自由端反射の場合とは完全に入れ替わった状態になります。シミュレーションで確認してみてください。
◎合成波のx方向,y方向に見た波長:
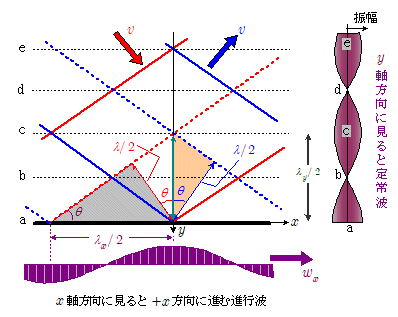
上図において,合成波を $x$ 軸方向, $y$ 軸方向に見たときの波長 $\lambda_x$ , $\lambda_y$ を調べてみましょう。
上図の薄い橙色の三角形に注目すると,青い実線と破線は反射波の山と谷を表しますので,その距離は本来の波長 $\lambda$ の半分 $\bun{\lambda}{2}$ です。よって $y$ 軸方向の半波長 $\bun{\lambda_y}{2}$ は,\[\bun{\lambda}{2} = \bun{\lambda_y}{2}\cdot \cos\theta \\ \kern-1em \therefore \lambda_y = \bun{\lambda}{\cos\theta} \]となります。したがって,$y$ 軸方向には $\bun{\lambda_y}{2} = \bun{\lambda}{2\cos\theta}$ ごとに『腹線』(振幅最大の波の通り道となる線)ができることになります。
一方 $x$ 軸方向には進行波ができますが,上図の灰色の三角形部分に注目すると,\[\bun{\lambda}{2} = \bun{\lambda_x}{2}\cdot \sin\theta \\ \kern-1em \therefore \lambda_x = \bun{\lambda}{\sin\theta} \]となります。よって $x$ 軸方向に移動する進行波の速度を $w_x$ とすると,振動数は $f$で変わりませんから, \[w_x = f\times \lambda_x \\ \kern1em = f\times \bun{\lambda}{\sin\theta} \\ \kern1em = \bun{f\times \lambda}{\sin\theta} = \bun{v}{\sin\theta} \]となります。これは平面波が $x$ 軸に沿って進んでいく速さにほかなりません。
数式を使った詳しい説明は,『参考 数式による平面波の干渉』の項を参照してください。
シミュレーションへ戻る
解説 2(全反射)
解説 3(振幅反射率・振幅透過率)
解説 4(エネルギー反射率・エネルギー透過率)
参 考 (数式による平面波の干渉)