屈折率の異なる媒質の境界面に波が入射すると,一般に屈折波と反射波を同時に生じますが,反射波は生じても屈折波を生じない場合があります。屈折角は $90^\circ$ 以上にはなり得ませんので,このような状況では屈折波はできず,波はすべて完全に反射することになります。この現象が『全反射』です。
以下,少し式を使って説明します。
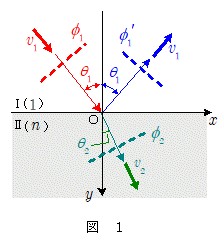
上図のように,媒質 $\mathrm{I}$ と媒質 $\mathrm{II}$ とが $x$ 軸に沿って接しているとします。
媒質 $\mathrm{I}$ の方から入射角 $\theta_1$ で平面波(赤波面)が入射し,境界面( $x$ 軸上)で反射波(青波面)と屈折波(緑波面,屈折角 $\theta_2$ )を生じたとします。
媒質 $\mathrm{I}$ に対する媒質 $\mathrm{II}$ の屈折率(媒質 $\mathrm{I}$ の屈折率を $1$ としたときの媒質 $\mathrm{II}$ の屈折率)を $n$ ,媒質 $\mathrm{I}$ での波の速さを $v_1$ ,媒質 $\mathrm{II}$ での波の速さを $v_2$ とすると,屈折の法則(スネルの法則)より,\[1 \times \sin\theta_1 = n\times \sin\theta_2 \quad\cdots\cdots\maru{1} \\ 1 \times v_1 = n \times v_2 \kern3em\cdots\cdots\maru{2} \] が成り立ちます。
まず$\maru{1}$ 式より,\[\sin\theta_2 = \bun{\sin\theta_1}{n}\]ですが, $\theta_2$ の $\sin$ は当然 $1$ 以下ですから, \[ \sin\theta_2 = \bun{\sin\theta_1}{n} \, \le 1 \\ \kern-1em \therefore \color{red}{\sin\theta_1 \le n \quad\cdots\cdots\maru{3} }\] の関係が成り立っていなければなりません。この $\maru{3}$ 式が,屈折波が生じるための入射角 $\theta_1$ の条件式になります。
ここで $\sin\theta_1 \le 1$ ですから,もし $1 \le n $ であるなら, \[\sin\theta_1 \le 1 \le n \] となり,すべての入射角 $\theta_1$ は $\maru{3}$ 式を満たすこととなり, $1 \le n $ の場合には必ず屈折波を生じることになります。
一方, $n \lt 1$ の場合, $\maru{3}$ 式より, \[\sin\theta_1 \le n \, \lt 1 \] となり,$\sin\theta_1$ の上限値は $n$ になってしまいます。 \[\color{red}{\underline{\sin\theta_1 = n}} \] を満たす入射角のことを臨界角といいます。入射角が臨界角のとき, $\maru{1}$ 式より,\[\sin\theta_2 = 1\quad \therefore \theta_2= 90^\circ \]となるので,簡単に言えば臨界角とは屈折角が $90^\circ$ になるような入射角…ということになります。
以上より, $ n \lt 1$ の場合, $ \sin\theta_1 \gt n$ なる入射角に対しては屈折波は存在せず,波はすべて反射してしまうことになります。これが『全反射』です。
シミュレーションへ戻る
解説 1(平面波の反射)
解説 3(振幅反射率・透過率)
解説 4(エネルギー反射率・透過率)
参 考 (数式による平面波の干渉)