◎2次元媒質中を伝わる波の強さ(エネルギー):
図1のような1次元媒質(弦など)における波の強さ(1点を単位時間に通過する波のエネルギー) $I$ は,『1次元媒質での反射波と透過波』の 『解説:波のエネルギー 』の項で解説しているように,媒質の線密度 $\rho_{線}$ ,波の振動数 $f$ の2乗,振幅 $A$ の2乗,および波の速度 $v$ に比例します。 \[I \, \propto \,\rho_{線} \, f^2 \, A^2 \, v \] 次に,2次元媒質(平面状の媒質)上を,図2のような同一位相面が直線状の波(山や谷が直線状になっている波。以下,「平面波」と呼ぶことにします)が進行している場合について考えます。媒質の面密度を $\rho_{面}$ ,この媒質上を伝わる波の速さを $v$ ,平面波の振動数を $f$ ,振幅を $A$ ,波の幅を $d$ とします。
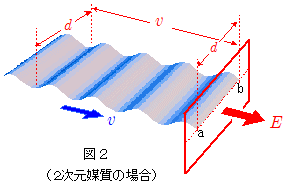
このとき,1次元媒質の場合との類推から容易に推察できるように,波の進行方向に垂直な長さ $d$ の直線 ( 図2の線分a b。 $\overline{\mathrm{a\,b}} = d $ )上を単位時間に通過する波のエネルギー $E$ は,上式の線密度$\rho_{線}$を面密度 $\rho_{面}$ に置き換え,さらに線分a bの長さ $d$ を考慮して,\[E \propto \,(\,\rho_{面} \, f^2 \, A^2 \, v\,)\times d \quad\cdots\cdots\Maru{13}\]となります。
◎エネルギー反射率,エネルギー透過率:
図3のように,平面状の媒質ⅠとⅡが $x$ 軸を境界線として接していて,媒質Ⅰの方から$x$ 軸上の $\mathrm{a\,b}$ に向かって平面波が入射角 $\theta_1$ で入射し,反射波と屈折波とを生じているとします。反射角は入射角と同じく $\theta_1$ であり,屈折角は $\theta_2$ とします。
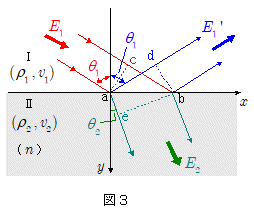
媒質I,Ⅱの面密度をそれぞれ $\rho_1$ , $\rho_2$ とし,またそれぞれの媒質での波の速度を $v_1$ , $v_2$ とすると,媒質Ⅰに対する媒質Ⅱの屈折率 $n$ は $n = \bun{v_1}{v_2}$ となります。
波の振動数を $f$ ,入射波の振幅を $A$ ,反射波の振幅を $B$ ,屈折波の振幅を $C$ とすると, $x$ 軸上の $\mathrm{a\,b}$ に入射する入射波,その反射波,屈折波によって単位時間あたりに運ばれる波のエネルギー $E_1$ , $E_1\,'$ , $E_2$ は,それぞれの波の進行方向に垂直な線分 $\overline{\mathrm{a\,c}}$ , $\overline{\mathrm{b\,d}}$ , $\overline{\mathrm{b\,e}}$ を通過する波のエネルギーを考えて,\[E_1 \propto \,\rho_1 \, f^2 \, A^2 \, v_1\times \overline{\mathrm{a \,c}} \\ \quad = \rho_1 \, f^2 \, A^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos (\angle\mathrm{bac}) \\ \quad = \rho_1 \, f^2 \, A^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos \theta_1 \\ E_1\,' \propto \,\rho_1 \, f^2 \, B^2 \, v_1\times \overline{\mathrm{b \,d}} \\ \quad = \rho_1 \, f^2 \, B^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos (\angle\mathrm{abd}) \\ \quad = \rho_1 \, f^2 \, B^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos \theta_1 \\ E_2 \propto \,\rho_2 \, f^2 \, C^2 \, v_2\times \overline{\mathrm{b \,e}} \\ \quad = \rho_2 \, f^2 \, C^2 \, v_2\times \overline{\mathrm{a \,b}}\cdot \cos (\angle\mathrm{abe}) \\ \quad = \rho_2 \, f^2 \, C^2 \, v_2\times \overline{\mathrm{a \,b}}\cdot \cos \theta_2 \]となります。
いま $E_1\,'$ , $E_2$ が $E_1$ の何倍になっているかを表す量をエネルギー反射率,エネルギー透過率と定義し,それぞれ $R$ , $T$ で表すと,\[ R = \bun{E_1{}'}{E_1} = \bun{\rho_1 \, f^2 \, B^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos \theta_1}{\rho_1 \, f^2 \, A^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos \theta_1} \\ \quad\quad\quad\quad = \bun{B^2}{A^2} \\ \quad\quad\quad\quad = r^2 \\ T = \bun{E_2}{E_1} = \bun{\rho_2 \, f^2 \, C^2 \, v_2\times \overline{\mathrm{a \,b}}\cdot \cos \theta_2}{\rho_1 \, f^2 \, A^2 \, v_1\times \overline{\mathrm{a \,b}}\cdot \cos \theta_1} \\ \quad\quad\quad\quad = \bun{\rho_2}{\rho_1}\cdot \bun{v_2}{v_1}\cdot\bun{C^2}{A^2}\cdot\bun{\cos\theta_2}{\cos\theta_1} \\ \quad\quad\quad\quad = \bun{\rho_2}{\rho_1}\cdot \bun{v_2}{v_1}\cdot t^2 \cdot\bun{\cos\theta_2}{\cos\theta_1}\] ここで $r$ , $t$ は $\Maru{11}$ 式, $\Maru{12}$ 式で示される振幅反射率,振幅透過率である。
いま平面状媒質として,『 波のシミュレーション』のページで取り扱ったような媒質(微小質点が網目状に配置されているような媒質)を考えるとすれば,この媒質上を伝わる波の速さ $v$ は媒質の面密度の平方根に反比例します。詳しくは 『波のシミュレーション』の 解説:本シミュレーションについて の項を参照してください。このページに記された $\Maru{\mathrm{A}}$ 式より,\[v \propto \,\bun{1}{\kon{\rho}} \quad\therefore \rho \propto \, \bun{1}{v^2} \\ \therefore \bun{\rho_2}{\rho_1} = \bigg( \bun{v_1}{v_2}\bigg)^2 \] この関係を上の $T$ の式に代入すると,\[T = \bun{\rho_2}{\rho_1}\cdot \bun{v_2}{v_1}\cdot t^2 \cdot\bun{\cos\theta_2}{\cos\theta_1} \\ \quad = \bigg( \bun{v_1}{v_2}\bigg)^2 \cdot \bun{v_2}{v_1}\cdot t^2 \cdot\bun{\cos\theta_2}{\cos\theta_1} \\ \quad = \bun{v_1}{v_2}\cdot t^2 \cdot\bun{\cos\theta_2}{\cos\theta_1} \\ \quad = n \cdot t^2 \cdot\bun{\cos\theta_2}{\cos\theta_1}\] ただし, $n = \bun{v_1}{v_2}$ を用いた。
さらに先の $\Maru{11}$ 式, $\Maru{12}$ 式で示される $r$ , $t$ をエネルギー反射率 $R$ ,エネルギー透過率 $T$ に代入していくと,\[\color{red}{R} = r^2 \\ \quad = \color{red}{ \bun{ (\cos\theta_1 - n\cdot \cos\theta_2 )^2}{ (\cos\theta_1 + n\cdot\cos\theta_2 )^2}}\quad \cdots\cdots\Maru{14} \\ \color{red}{T} = n \cdot t^2 \cdot\bun{\cos\theta_2}{\cos\theta_1} \\ \quad = n \cdot \bigg( \bun{2 \cos\theta_1 }{\cos\theta_1 + n\cdot\cos\theta_2} \bigg) ^2 \cdot\bun{\cos\theta_2}{\cos\theta_1} \\ \quad = \color{red}{ \bun{4\,n\, \cos\theta_1\cdot \cos \theta_2}{ (\cos\theta_1 + n\cdot \cos\theta_2 )^2} } \quad \cdots\cdots\Maru{15} \] したがって $R$ と $T$ の和を考えると,\[R + T = \bun{ (\cos\theta_1 - n\cdot \cos\theta_2 )^2}{ (\cos\theta_1 + n\cdot\cos\theta_2 )^2} + \bun{4 \,n \, \cos\theta_1\cdot \cos \theta_2}{ (\cos\theta_1 + n\cdot \cos\theta_2 )^2} \\ \quad\quad\quad = 1 \\ \therefore \color{red}{ R + T = 1 } \quad \Rightarrow \quad \therefore \bun{E_1{}'}{E_1} + \bun{E_2}{E_1 } = 1 \\ \therefore E_1{}'+E_2 = E_1 \] 反射波と屈折波のエネルギーの和が入射波のエネルギーに等しいということは,波が反射と屈折の両方を生じる場合のエネルギー保存を表していることになります。
下の図4,図5は,振幅反射率・振幅透過率,およびエネルギー反射率・エネルギー透過率と入射角 $\theta_1$ との関係を表すグラフです。図4は屈折率 $n$ が $1$ より大きい場合($n = \bun{3}{2}$ ),図5は屈折率 $n$ が $1$ より小さい場合( $n = \bun{2}{3}$ )のグラフです。
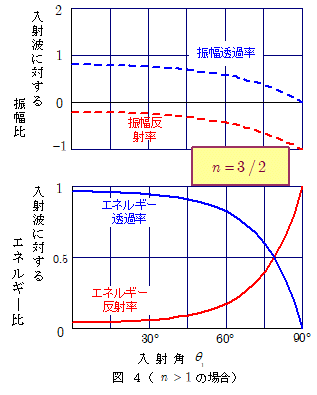
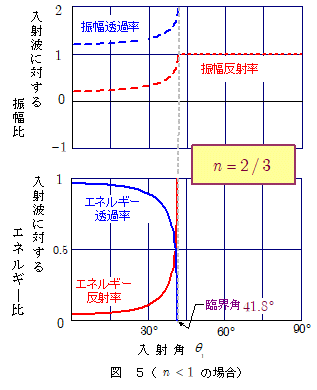
図5のように,屈折率 $n$ が $1$ より小さい場合( $n \lt 1$ ),入射角が臨界角に近づくと振幅透過率は増大して「 $2$ 」に近づいていくのに対し,エネルギー透過率の方は逆に急速に減少して「 $0$ 」に近づいていきます。振幅が増大すればエネルギー密度が大きくなるのだからエネルギー量も増えそうなのに,なぜエネルギー透過率が減少するのか,ちょっと奇異に感じるかもしれません。それは,入射角が臨界角に近づくにつれて透過波(屈折波)の幅が急速に狭く(細く)なっていき,そのために透過波として運ばれるエネルギー量であるエネルギー透過率が小さくなってしまうのです。ちなみに 入射角 → 臨界角 の極限においては透過波の幅は $0$ となり,透過波(屈折波)は存在しなくなります。これが「全反射」です。こうした透過波(屈折波)の幅の変化については,『シミュレーション』の方に戻って確認してみてください。
ちなみに,透過波の幅と入射波の幅の比は,図3において, \[ \bun{\overline{\mathrm{b\,e}}}{\overline{\mathrm{a\,c}}} = \bun{\cos\theta_2}{\cos\theta_1}=\bun{\kon{n^2-\sin\theta_1{}^2}}{n\cdot\cos\theta_1}\] ですから, $n \lt 1$ の場合, $\sin\theta_1 \rightarrow n$ で $ \bun{\overline{\mathrm{b\,e}}}{\overline{\mathrm{a\,c}}} \rightarrow 0 $ となります。
シミュレーションへ戻る
解説 1(平面波の反射)
解説 2(全反射)
解説 3(振幅反射率・透過率)
参 考 (数式による平面波の干渉)