→ライプニッツの公式へ戻る

(Leibnitzの公式の証明)　　

　　[『理工系の微分積分学』2章§1II(p.42);小平『解析入門I』§3.4定理3.11:証明付(p.127);
　　　　笠原『微分積分学』2.3[1]定理2.13:証明付(p.48)]
　　　　　　

　　　　nは自然数であるので、自然数の公理より、数学的帰納法で示すことができる。　　　　　

　　　　(i)　n =1のとき　　　　　　　

　　　　　（※）の左辺＝( f (x) g (x) ) ⁽¹⁾

　　　　　　　　　　　＝( f (x) g (x) ) '　　　　　　∵1階導関数は普通の導関数　(n階導関数の記法)　

　　　　　　　　　　　=f ' (x) g (x) ＋ f (x) g ' (x)　∵関数の積の微分公式　　　　

　　　　　　　　　　　　　∵_nC₀=1, ₁C₁=1(Combinationの定義)　

　　　　　　　　　　　=f ' (x) g (x) ＋ f (x) g ' (x)　　　

　　　　　　　　　　　∵0階導関数はもとの関数、1階の導関数は普通の導関数(n階導関数の記法)　

　　　　　　よって、n =1のとき、（※）が成立　　　　

　　　　(ii)　l >1として、 n =lのとき(※)が成り立つと仮定する。　　　　　　　

　　　　　　すなわち、　　…(1)　　

　　　　　　n = l + 1 のとき、　　　　　

　　　　　　　（※）の左辺＝( f (x) g (x) ) ^(l＋1) 　　　　

　　　　　　　　　　＝ [ ( f (x) g (x) ) ^{( l )} ]' 　　∵n階導関数の定義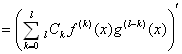　　　

　　　　　　　　　　　　∵(1)　　

　　　　　　　　　　　　　∵関数和の微分、関数の定数倍の微分　

　　　　　　　　　　　∵関数積の微分　

　　　　　　　　　　　　　　　　　　　　∵_nC₀=1, _nC_n=1(Combinationの定義)　　

　　　　　　　　　　　　　　　　　　　　　第二項のkの数え方をかえただけ　　

　　　　　　　　　　　　　　　∵n個の組合せと(n−1)個の組合せを関係付ける漸化式より　　

　　　　　　　　　　　　　　　　　　　　　_l+1C_k= _lC_k ＋_lC_kｰ1　

　　　　　　　　　　　　　　　　　　　　∵_nC₀=_nC_n=1(Combinationの定義)　

　　　　　　　よって、n = kで（※）が成立するならば、n = k＋１でも（※）は成立。　　　　

　　　　(i) (ii)から、(※)は全ての自然数nについて成立する。