チャレンジ！数学

のりちゃんのデジタル教材『チャレンジ！数学』の特徴

◎　数学が大好きになるデジタル教材です。

◎　楽しい！わかりやすい！の声が教室に響き渡ります。

◎　ノートにまとめやすいように構成しています。

◎　生徒一人一人の理解度をチェックする時間が生まれます。

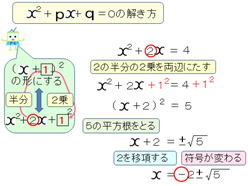
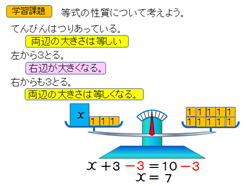
平成２６年６月から平成２７年３月にかけて、愛媛大学教育学部附属中学校で、非常勤講師として、数学の授業を担当する機会を得ました。数学の免許はもっていましたが、中学生に数学を教えるのは初めてでしたので、私にとってチャレンジそのものでした。

のりちゃんのデジタル教材が本当に生徒の理解に役立つのか、わくわくしながら教壇に立ちました。

一日の授業が終われば、パソコンに向かって次の授業のデジタル教材づくり。教科書を見て、生徒の学習意欲を高めるための内容構成を考えながらスライドを作成します。チャレンジの連続です。教材研究をしているのと同じですので、デジタル教材ができあがると余裕をもって授業に臨むことができました。

生徒の数学への興味・関心も高まったようで、「パソコンの授業は楽しい」「数学が好きになった」「すらすら頭に入ってきた」「ノートがまとめやすかった」「数学が苦手な私もすぐに解ける問題が増えてきた」などの感想を色紙に書いて贈ってくれました。

１年生と３年生の実践例がたくさんできました。

たくさんの方々に利用していただき、数学好きの生徒を育てていただきたいと考えています。

ダウンロードできるデジタル教材

中学１年生

等式の性質を使って、一次方程式を解く	教材（パワーポイント）
移項して一次方程式を解く　その１	教材（パワーポイント）
平行移動	教材（パワーポイント）

中学３年生

解の公式を使って、二次方程式を解く　その１	教材（パワーポイント）
因数分解を使って、二次方程式を解く　その１	教材（パワーポイント）
円の性質の利用　その１	教材（パワーポイント）

『チャレンジ！数学』のデジタル教材集の内容

中学１年生

単元名		指　　導　　内　　容	教材（パワーポイント）	ワークシート
文字の式		マグネットの個数をｘを使って表す	○
方程式	方程式とその解	等式の性質を理解する	○
	方程式とその解	等式の性質を使って、一次方程式を解く	○
	方程式の解き方	移項して解く方法を見つけ、一次方程式を手際よく解く	○
		文字の項を移項して、一次方程式を解く	○
		かっこをはずしたり、分母をはらったりして一次方程式を解く	○
		いろいろな一次方程式を解く	○
	比と比例式	比例式の意味がわかり、比の値を使って比例式を解く	○
	比と比例式	比例式の性質を見つけ、比例式の性質を使って比例式を解く	○
	方程式の利用	方程式を利用して、実際の問題を解く　その１	○
		方程式を利用して、実際の問題を解く　その２	○
		方程式を利用して、実際の問題を解く　その３	○
		方程式を利用して、実際の問題を解く　その４	○
変化と対応	関数	伴って変わる数量の関係を調べる	○	○
	比例の式	比例の関係を見つけ、それを式に表す	○
	比例の式	比例の関係で、負の数まで変数の範囲を広げる	○
	座標	平面上の点の位置を表す方法を知る	○
	比例のグラフ	比例の関係をグラフに表す　その１	○	○
		比例の関係をグラフに表す　その２	○	○
		比例の関係をグラフに表す　その３	○	○
	反比例の式	反比例の関係を見つけ、それを式に表す	○
	反比例の式	反比例の関係で、負の数まで変数の範囲を広げる	○
	反比例のグラフ	反比例の関係をグラフに表す　その１	○	○
	反比例のグラフ	反比例の関係をグラフに表す　その２	○	○
平面図形	直線と角	直線と角の意味を理解する	○
	直線と角	垂直と平行の意味を理解する	○
	図形の移動	平行移動の意味を理解し、平行移動した図形を作図する	○
		回転移動の意味を理解し、点対称移動した図形を作図する	○
		対称移動の意味を理解し、対称移動した図形を作図する	○
	基本の作図	線分の垂直二等分線を作図する	○
		角の二等分線を作図する	○
		垂線を作図する	○
	円とおうぎ形の性質	円の弧と弦、中心角を知る円の接線の性質を理解し、接線を作図する	○
	円とおうぎ形の性質	おうぎ形を調べる	○
	円とおうぎ形の計量	円とおうぎ形について、円周や弧の長さ、面積を求める　その１	○
		円とおうぎ形について、円周や弧の長さ、面積を求める　その２	○
		円とおうぎ形について、円周や弧の長さ、面積を求める　その３	○
空間図形	いろいろな立体	いろいろな立体の特徴を調べる	○
	空間内の平面と直線	平面や直線の位置関係について考える　その１	○
		平面や直線の位置関係について考える　その２	○
		２平面の位置関係について考える	○
	立体のいろいろな見方	立体をいろいろな見方でとらえる　その１	○
	立体のいろいろな見方	立体をいろいろな見方でとらえる　その２	○
	立体の表面積	角柱、円柱の表面積を求める	○
	立体の表面積	角錐、円錐の表面積を求める	○
	立体の体積	角柱、円柱の体積を求める	○
	立体の体積	角錐、円錐の体積を求める	○
	球の計量	球の体積・表面積を求める	○
資料の活用	度数分布	度数分布表を作成し、考察する	○	○
		資料をヒストグラムと度数分布多角形に表す	○	○
		相対度数の求め方を理解し、度数分布多角形に表す	○	○
	代表値と散らばり	資料から平均値を求める	○
		資料から中央値を求める	○
		資料から最頻値を求める	○
		資料の分布のようすと平均値、中央値、最頻値の関係を見る	○	○
		資料の傾向を散らばりから考察する	○
	近似値	測定などによって得られた数の表し方を知る	○

中学２年生

単元名		指　　導　　内　　容	教材（パワーポイント）	ワークシート
式の計算	式の加法、減法	同類項をまとめて、式を簡単にする	○
	いろいろな多項式の計算	分配法則を使って、式を簡単にする。	○
	いろいろな多項式の計算	式を簡単にしてから、式の値を求める。	○
	単項式の乗法、除法	文字式×文字式の計算をする。	○
	単項式の乗法、除法	文字式÷文字式の計算をする。	○
連立方程式	連立方程式の解き方	連立方程式を加減法で解く。その１	○
		連立方程式を加減法で解く。その2	○
		連立方程式を代入法で解く。	○
		いろいろな連立方程式を解く。	○
		連立方程式の練習問題	○
	連立方程式の利用	実際の問題を連立方程式を利用して解く。その１	○
		実際の問題を連立方程式を利用して解く。その２	○
		実際の問題を連立方程式を利用して解く。その３	○
		実際の問題を連立方程式を利用して解く。まとめ	○
一次関数	一次関数	ともなって変わる２つの数量の間の関係をとらえる。	○
	一次関数の値の変化	一次関数の値の変化について調べる。その１	○
	一次関数の値の変化	一次関数の値の変化について調べる。その２	○
	一次関数のグラフ	一次関数をグラフに表し、その特徴を調べる。その１	○	○
		一次関数をグラフに表し、その特徴を調べる。その２	○	○
		一次関数をグラフに表し、その特徴を調べる。その３	○	○
	一次関数の式	一次関数のグラフから、その関数の式を求める。その１	○	○
		一次関数のグラフから、その関数の式を求める。その２	○
		一次関数のグラフから、その関数の式を求める。その３	○
		一次関数のグラフから、その関数の式を求める。まとめ	○
	方程式とグラフ	二元1次方程式の解をグラフに表す。その１	○	○
	方程式とグラフ	二元1次方程式の解をグラフに表す。その２	○	○
	一次関数の利用	一次関数を利用して、身のまわりの問題を解決する。その１	○	○
		一次関数を利用して、身のまわりの問題を解決する。その２	○	○
		一次関数を利用して、身のまわりの問題を解決する。その３	○	○
		一次関数を利用して、身のまわりの問題を解決する。まとめ	○	○
図形の調べ方	角と平行線	直線が交わってできる角について調べる。その１	○
	角と平行線	直線が交わってできる角について調べる。その２	○
	多角形の角	三角形や多角形の角の性質を調べる。その１	○
		三角形や多角形の角の性質を調べる。その２	○
		三角形や多角形の角の性質を調べる。その３	○	○
	三角形の合同	2つの三角形は、どんな場合に合同のなるか考える。	○

中学３年生

単元名		指　　導　　内　　容	教材（パワーポイント）	ワークシート
平方根		有理数と無理数を数直線上に表す	○	○
二次方程式	二次方程式とその解き方	日常の事象を使って二次方程式をつくり、解が２つあることを知る	○
		二次方程式を平方根の意味にもとづいて解く　その１	○
		二次方程式を平方根の意味にもとづいて解く　その２	○
		二次方程式を平方根の意味にもとづいて解く　その３	○
	二次方程式の解の公式	平方根の意味にもとづいて解く過程と対比しながら、二次方程式の解の公式を導き出す	○
		解の公式を使って二次方程式を解く　その１	○
		解の公式を使って二次方程式を解く　その２	○
	二次方程式と因数分解	因数分解を使って二次方程式を解く　その１	○
		因数分解を使って二次方程式を解く　その１	○
		二次方程式をいろいろな方法で解き、それぞれの長所を知る	○
	二次方程式の利用	二次方程式を利用して問題を解く　　その１	○
		二次方程式を利用して問題を解く　　その２	○
		二次方程式を利用して問題を解く　　その３	○
関数	関数とグラフ	の式に表す　その１	○
		の式に表す　その２	○
		をグラフに表す　その１	○
		をグラフに表す　その２	○	○
		をグラフに表す　まとめ	○
	変化の割合	関数の値の変化のようすについて調べる	○	○
	変化の割合	関数の変化の割合について調べる	○	○
	いろいろな事象と関数	身の回りにある関数について調べる	○
	いろいろな事象と関数	いろいろな関数について調べる	○
図形と相似	図形と相似	相似な図形の意味や性質について理解する	○
		相似な図形の辺の長さを求める	○
		三角形の相似条件について調べる　その１	○	○
		三角形の相似条件について調べる　その２	○
		三角形の相似条件を使った証明問題を解く　その１	○	○
		三角形の相似条件を使った証明問題を解く　その１	○
	平行線と線分の比	平行線と線分の比の関係をとらえる　その１	○
		平行線と線分の比の関係をとらえる　その２	○
		平行線と線分の比の関係をとらえる　その３	○
	中点連結定理	中点連結定理を理解し、活用する　その１	○
	中点連結定理	中点連結定理を理解し、活用する　その２	○
	相似な図形の計量	相似な図形の面積の関係を理解し、活用する　その１	○
		相似な図形の面積の関係を理解し、活用する　その２	○
		相似な立体の表面積・体積の関係を理解し、活用する　その１	○
		相似な立体の表面積・体積の関係を理解し、活用する　その２	○
	相似の利用	相似の考え方をいろいろな場面で利用する	○
円の性質	円周角と中心角	円周上に点をとってできる角について調べる　その１	○
		円周上に点をとってできる角について調べる　その２	○
		円周上に点をとってできる角について調べる　その３	○
		円周角の定理の逆について調べる	○
	円の性質の利用	円の性質を使って問題を解決する　その１	○
		円の性質を使って問題を解決する　その２	○
		円の性質を使って問題を解決する　その３	○
三平方の定理	三平方の定理	直角三角形の３辺の長さの関係について考える　その１	○
		直角三角形の３辺の長さの関係について考える　その２	○
		三平方の定理の逆について調べる	○
	三平方の定理の利用	三平方の定理を利用して、線分の長さや面積を求める　その１	○
		三平方の定理を利用して、線分の長さや面積を求める　その２	○	○
		三平方の定理を利用して、線分の長さや体積を求める　その１	○
		三平方の定理を利用して、線分の長さや体積を求める　その２	○	○

３学年セットのデジタル教材集（ＣＤ）を実費（送料込み３,０００円）で販売いたします。興味・関心のある方は、ご連絡ください。