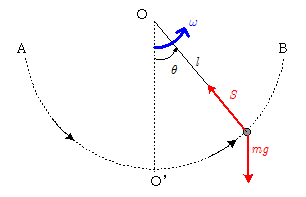
慣性モーメント $I$ の物体が力のモーメント $N$ を受けているときの回転の運動方程式は,角速度 $\omega$ として,\[\tdif{}(I\,\omega) = N \cdots\cdots\maru{1}\] であった。
以下では,人を,その全質量が人の重心に集中した質点と簡単化して考えることとする。
さて,ブランコをこぐとき,人は立ったりしゃがんだりする。このことによって,ブランコの支点と人の重心との距離,つまり上図でいえば糸の長さ $l$ が変化し,したがって慣性モーメントが変化することになる。このため,$\maru{1}$ 式にしたがった角速度 $\omega$ の変化が生じることになる。
糸の長さが $l$ であるとき,質点の支点Oに関する慣性モーメントは $I=m\,l^2$ と表されるので, $\maru{1}$ 式は,以下のように式変形される。
なお上図の位置において,支点Oのまわりの質点(この場合は人)に働く重力のモーメント $N$ は, $N = -m\,g\,l\sin\theta$ である。\[\dif{}{t}(I\omega)=N\\ \kern-1em \therefore \dif{}{t}(m\,l^2\,\omega)=-m\,g\,l\sin\theta \\ \kern-1em \therefore 2m\,l\dif{l}{t}\omega + m\,l^2\dif{\omega}{t}=-m\,g\,l \sin\theta\\ \kern-1em \therefore \dif{\omega}{t}=-\bun{g}{l}\sin\theta - 2\bun{\omega}{l}\dif{l}{t}_{(a)} \cdot\cdots\maru{2} \] $\bun{\mathrm{d}\omega}{\mathrm{d}t}$は小球の角加速度で,これに距離 $l$ を乗じた値が小球の接線加速度である(接線加速度 $=l\,\tdif{\omega}$ ) 。
ここで大事なのは, $\maru{2}$ 式の第2項 $(a)$ の存在である。
もしこの項がなければ,\[\dif{\omega}{t}=-\bun{g}{l}\sin\theta \\ \kern-1em \therefore \left \{ \begin{array}{rl} & \kern-1em \theta>0 \rightarrow \tdif{\omega}<0 \\ & \kern-1em \theta<0 \rightarrow \tdif{\omega}>0 \end{array} \right . \]となり,小球は $\theta$ が負から正,逆に正から負になるごとに,つまり半周期ごとに加速されたり減速されたりを繰り返すだけで,全体としては少しも振れは大きくはなっていかない。
では,$\maru{2}$ 式右辺第2項 $(a)$ の効果・影響はどのようなものであるか,その振る舞いについて考えてみよう。
この項には $\tdif{l}$ という因子が含まれている。この因子が,重要な役割を演じるのである。
この因子の存在により,支点Oからの距離 $l$ を時間変化させると角加速度 $\tdif{\omega}$ の値が変わるということを意味している。つまり「ブランコをこぐ」とは,しゃがんだり立ち上がったりすることによってブランコの支点と人の重心との距離 $l$ を時間変化させ, $\tdif{l}$ を生じさせているのである。
いま,図の $\mathrm{A~O'}$ 間( $\theta \lt 0$)にあって,反時計回りの向きに回転している( $\omega>0$ )場合について考えてみよう。
この範囲では $\theta \lt 0$ ゆえ $-\bun{g}{l}\sin\theta>0$ である。よって $\tdif{l} \lt 0$ ,つまり距離 $l$ が減少していけば(人が立ち上っていけば), 第2項 $(\mathrm{a})$ も $- 2\bun{\omega}{l}\dif{l}{t} \gt 0$ となり,右辺第1項,第2項ともに正となるので $\tdif{\omega}>0$ となり,小球は加速されていくことになる。
しかもその値は $\omega$ が大きく,かつ $\big|\mathrm{d}\,l/\mathrm{d}\,t \big|$ が大きい ほど効果的である。つまり,ブランコが下方に降下してきて $\omega$ が大きくなったとき,なるべく急速に $l$ を小さく(素早く立ち上がる)していけばよいことになる。
つぎに最下点 $\mathrm{O}'$ を越えて上昇していく場合を考えよう。
この場合 $\theta>0$ ゆえ $-\bun{g}{l}\sin\theta<0$ であり,この項の効果により $\tdif{\omega}$ は全体として負となって,小球は減速されていくことになる。
しかし, $\tdif{\omega}$ の絶対値がなるべく小さければ減速のされ方が弱くなり,より高いところに達することができるようになる。
この場合も,第2項 (a)が正であれば $\tdif{\omega}$ の絶対値を小さくすることはできるはずである。そのためにはやはり $\tdif{l}$ が負であり続ければよい。つまり立ち上がり続ければよいことになる。
そして最高点に達した瞬間に今度は急にしゃがみ込み,$l$ を大きくする。このとき $\omega=0$ であるから,第2項(a)の効果は $0$ である。
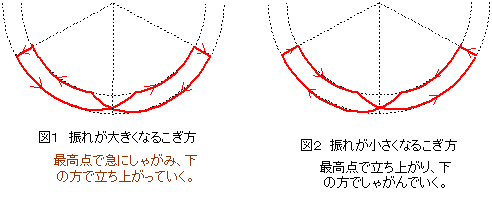
戻ってくる場合( $\omega<0$ )も同様に,下方で立ち上がり,最高点でしゃがみ込む。以後,この動作を繰り返すことによって,ブランコの振れはどんどん増大していくことになる。
◎エネルギーの供給はどの過程で行われるか?
ブランコの振れが大きくなるためには,エネルギーの供給がなくてはならないはずである。しかし,外から誰かが押しているわけでもないし,ブランコに乗っている人が単に立ったりしゃがんだりの動作を繰り返しているに過ぎない。なのに,振れは大きくなっていく・・・
実は,下方の位置で立ち上がり,上方でしゃがむ・・という,立つ,しゃがむというモーションを起こす位置の違いが,エネルギー供給を生む元なのである。
下方では角速度が大きく,大きな遠心力がはたらく。したがってこの位置で立ち上がっていくには,重力のほかに,遠心力にも逆らって人は「仕事をする」必要がある。一方しゃがむとき,人は重力と遠心力によって「仕事をなされる」ことになるが,この「する仕事」と「なされる仕事」が等しければ,全体として人のする仕事は $\pm 0$ となり,ブランコの系の力学的エネルギーの増減はなく,振れ幅も変化しない。
しかし,上方ほど角速度が小さく遠心力も小さいので,上方でしゃがむようにすれば人が「なされる」仕事は小さいことになる。
結局,遠心力の大きい下方で立ち上がり,遠心力の小さい上方でしゃがめば,遠心力の大小によって「する仕事」と「なされる仕事」の量に差が生じることとなり,差し引き,人はブランコの系全体に対して「正の仕事」をしたことになり,その力学的エネルギーが増大して振れ幅が大きくなっていくのである。
ブランコをこぐ際のエネルギー面からの考察については,「横国入試問題」を参考にしてください。
以上より,ブランコを効率良くこぐには,上でしゃがみ,下で立ち上がるのがよいと結論できることになる。