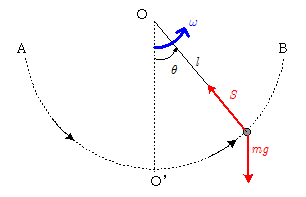
上図のように，長さ $l$ の糸の先端に質量 $m$ の小球が結びつけられた単振り子の運動方程式は，以下のようになる。（詳しくは「単振り子の解説」を参照。）\[ m\,l\dif{\theta^2}{t^2}=m\,l\dif{\omega}{t}=-m\, g \sin\theta \] 　ただし，角速度 $\omega=\dif{\theta}{t}$ （回転角の変化スピード），したがって $\dif{\omega}{t}$ は角速度の時間変化量，すなわち角加速度である。 　さらに上式の両辺に長さ $l$ を乗じると，\[m\,l^2\dif{\omega}{t}=-m\,g \, l\sin\theta\] 　ここで，上式の右辺 $-m\,g \, l\sin\theta$ は，この振り子にかかる重力の支点Ｏのまわりのモーメント $N$ にほかならない。また左辺の $\displaystyle\dif{\omega}{t}$ にかかる係数 $m\,l^2$ は，この場合における小球の支点Ｏのまわりの慣性モーメントと呼ばれる物理量で，一般に $I$ などの文字で表す。よって上式は\[I\dif{\omega}{t}=N\cdots (\mathrm{i})\]と書ける。これがこの小球の点Ｏのまわりの回転に関する運動方程式となる。
　物体の並進運動における運動方程式 　$m\dif{v}{t}=力 F$ 　と比較すると，\[角加速度 \dif{\omega}{t}\quad \rightleftarrows 加速度 \dif{v}{t} \\ 慣性モーメント I\quad \rightleftarrows \quad質量 m \\ 力のモーメントN \quad \rightleftarrows \quad 力 F\] という対応が成り立つ。
　ところで(i)式は，慣性モーメント $I$ が変化しない場合にのみ成立する式である。本ケースの場合であれば $I=m\,l^2$ であるので，糸の長さ $l$ が変化すれば $I$ の値が変化することになる。このように慣性モーメントも変化する場合は，(i)式をさらに拡張する必要がある。

　 $\omega$ も $I$ も時間変化する可能性がある場合は， $I$ の時間変化の影響を考慮して，(i)式は次のように書き直されることになる。\[I\tdif{\omega} + \tdif{I}\omega=N \] 　以上より，一般に回転に関する運動方程式は，以下のように表すことができる。\[\tdif{}(I\,\omega)=N\] 　ここで，慣性モーメントと角速度の積 $L=I\omega$ で表される物理量を角運動量という。この角運動量を用いて表すと，次のようにまとめることができる。

　角運動量の時間変化は，力のモーメントに等しい。\[\color{red}{\dif{L}{t}=\bun{\mathrm{d}}{\mathrm{d}t}(I\omega)=N }\cdots\cdots\maru{1} \] 　上式は固定された回転軸を有する物体の場合であるが，回転軸を持たない物体の場合についても上記の関係は成り立つ。詳細は後述（ここをクリック）。