◎角運動量について:
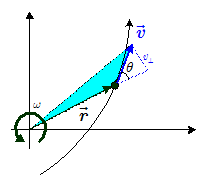
質量 $m$ の物体の位置 $\Vec{r}$ での速度が $\Vec{v}$ であるとき, $\Vec{L}=\Vec{r} \times m \Vec{v}$ なる物理量をこの物体の
角運動量という。角運動量の時間微分をしてみると, \[\tdif{\Vec{L}}=\tdif{}(\Vec{r} \times m \Vec{v})\\ \quad\quad =\tdif{\Vec{r}}\times m \Vec{v} + \Vec{r} \times \tdif{(m\Vec{v})} \\\quad\quad =\Vec{v} \times m \Vec{v}+\Vec{r} \times m\tdif{\Vec{v}}\]
ここで2つのベクトルの積 $\Vec{A}\times \Vec{B}$ をベクトルの外積(ベクトル積ともいう)といい,その大きさ $\vert\Vec{A}\times \Vec{B}\vert$ は,2つのベクトルの互いに直角な成分同士の積である。したっがて,同じベクトルどうしの外積は $0$ となる。これより, $\Vec{v} \times m \Vec{v} \equiv 0$ ,したがって上式右辺第1項は $0$ である。また運動方程式より, $m\bun{d\Vec{v}}{dt}=\Vec{F}$ であるから,上式は \[\tdif{\Vec{L}}=\Vec{r} \times m\tdif{\Vec{v}}\\\quad\quad =\Vec{r} \times \Vec{F} \\\quad\quad = 力のモーメント \Vec{N} \]
なる関係が導かれる。
ここで角運動量の大きさ$\vert\Vec{L}\vert$は,\[\vert\Vec{L}\vert=\vert\Vec{r} \times m \Vec{v}\vert=\vert\Vec{r}\vert \cdot m \vert\Vec{v}\vert\sin\theta \]
ただし, $\theta$ は $\Vec{r}$ と $\Vec{v}$ とがなす角である。ここで上図において質点の原点Oのまわりの角速度を $\omega$ とすると, \[\vert\Vec{v}\vert\sin\theta=v_\perp=r \omega\]であることから, \[\vert\Vec{L}\vert=\vert\Vec{r}\vert \cdot m \vert\Vec{v}\vert\sin\theta=m r^2\omega = I\,\omega \\[1.3em] (ただし,I=m\,r^2=慣性モーメント) \]
となり,さきの $\maru{1}$ 式が得られる。
力のモーメント $\Vec{N}=0$ であるとき, $\tdif{\Vec{L}}=0\quad\therefore \Vec{L}=一定$ となる。このとき,
角運動量が保存されているという。
また, $\bun{\vert\Vec{L}\vert}{2m}=\bun{1}{2}\vert\Vec{r} \times \Vec{v}\vert$ となり,これは上図青色部分の三角形の面積に等しく,これを
面積速度という。角運動量は面積速度を2倍して質量をかけた量であるから,角運動量が保存されるとき面積速度も一定に保たれる。これを
面積速度一定の原理という。
