振幅が増大するのは人間が何らかの仕事をして,ブランコと人間の系の力学的エネルギーを増大させるからである。振幅が増加する様子を次の仮定のもとで解析しよう。
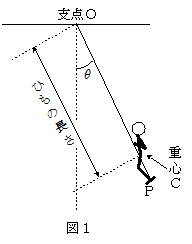
まず,ブランコの質量は無視し,また,ひもは曲がらないとする。支点Oで摩擦はなく,空気抵抗なども考えなくてよいとする。人間を重心Cに質量の集中した質点で近似する。図1に示すように,支点Oから人間の重心Cまでの距離をひもの長さと呼ぶことにし,重心Cは直線OPからはずれることはないとする。
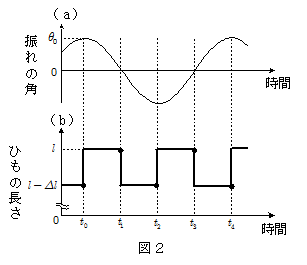
ブランコに乗っている様子を想像してみよう。ブランコをこぐとき,振れの角 $\theta$ が極大または極小ではひざを曲げる。ひざを曲げ腰を下げると重心は低くなり,ひもは長くなる。このときひもの長さは $l$ であるとする。次に,最下点 $(\,\theta=0\,)$ でひざを伸ばすと重心は高くなり,ひもは短くなる。このときひもの長さは $l-\varDelta l$ になるとする。結局,ひざの屈伸でひもの長さを変えていることがわかる。だから,ひざをす速く屈伸すれば,振れの角 $\theta$ とひもの長さは図2のように変化するだろう。ブランコが1往復するあいだに,ひもの長さは2回伸縮している。
ひもの長さと時間の関係を示す図2(b)で, $t_0$ ,$t_1$ ,$\cdots \cdots$ はひざを曲げる,あるいは伸ばす動作の直前の時刻をさすものとする。それらの時刻でのひもの長さは図2(b)の黒丸で示した。
次の $(1)$ から $(5)$ までの問に答えよ。ただし,振れの角 $\theta$ は十分小さいとして $\cos \theta \fallingdotseq 1-\theta{}^2/2$ と近似せよ。人間の質量を $m$ ,重力加速度を $g$ とする。解答には,$l$ , $\varDelta l$ , $m$ , $\theta_0$ , $N$ 以外の記号を用いてはいけない。
(1) 時刻 $t_0$ から $t_2$ までのあいだに人間がひざを屈伸することによって重力に抗してする仕事を求めよ。ブランコと人間の系の力学的エネルギーが増加するとき仕事の符号は正で,力学的エネルギーが減少するとき仕事の符号は負であるとする。時刻 $t_0$ での振れの角 を$\theta_0$ とする。
(2) 時刻 $t_1$ における,重心Cの速さを求めよ。
(3) 時刻 $t_0$ から$ t_2$ までのあいだに人間がひざの屈伸により遠心力にさからってする仕事を求めよ。ただし遠心力の大きさはひざを伸ばしたり,曲げたりするあいだ一定であると仮定し,屈伸を始める直前の重心Cの速さを用いて計算せよ。仕事の符号は $(1)$ と同じとする。
(4) 時刻 $t_2$ における振れの角の大きさを求めよ。
(5) ブランコが $N$ 回往復したときの振れの角の大きさを求めよ。
◎ 解 答:
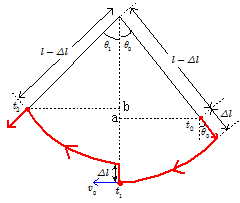
(1) 時刻 $t_0$ に膝を曲げ,このとき重力によって $m g \cdot \varDelta l \cos \theta_0$ の仕事をなされるので,人のする仕事 $W_{g,t_0}$ は,\[W_{g,t_0}=-m g \cdot \varDelta l \cos \theta_0\] 時刻 $t_1$ に人は立ち上がるので,このとき人が重力に逆らってする仕事 $W_{g,t_1}$ は,\[W_{g,t_1}=m g\cdot \varDelta l\] よって時刻 $t_0$ から時刻 $t_2$ までの間に人が重力に抗してした仕事 $W_g$ は,\[W_g=W_{g,t_0}+W_{g,t_1}=m g \cdot \varDelta l\cdot (-\cos \theta_0 + 1 ) \fallingdotseq \underline{m g\cdot \varDelta l \cdot \bun{\theta_0{}^2}{2} }\] (2) 時刻 $t_0$ 直後から時刻 $t_1$ 直前までの間では膝の屈伸はないので,力学的エネルギーが保存される。よって最下点での速さを $v_0$ とすると, \[\bun{1}{2}mv_0{}^2=mg\, l(1-\cos \theta_0) \fallingdotseq \bun{1}{2}m g \,l \cdot \theta_0{}^2 \\ \quad \therefore v_0=\underline{\kon{g l}\theta_0}\] (3) 人の速さが $0$ でない限り遠心力がはたらくが,遠心力は糸方向外向きにはたらくので,膝の屈伸がない限り遠心力に対する仕事の出入りはない。したがって遠心力に抗して仕事をするのは,最下点(時刻 $t_1$ )で立ち上がる瞬間のみである。よって遠心力に逆らってする仕事$W_{遠}$は, \[W_{遠}=m\bun{v_0{}^2}{l}\cdot \varDelta l \\ \quad = m\bun{(\kon{g \,l }\theta_0)^2}{l}\cdot \varDelta l\\ \quad =\underline{mg \cdot \theta_0{}^2 \cdot \varDelta l}\] (4) 時刻 $t_0$ に膝を曲げ始める直前から,時刻 $t_2$ に最高点に達するまでの力学的エネルギーの増加分 $\varDelta E$ は,この間に人がした仕事に等しい。 \[ \therefore \varDelta E = W_g+W_{遠} \] ここで,$t_0$ および時刻 $t_2$ において運動エネルギーは $0$ であることに留意すると,この間の力学的エネルギーの増加 $\varDelta E$ は,図のab間のの高低差にもとづく位置エネルギーに等しい。\[\varDelta E = \varDelta U \\ \quad = mg\cdot \overline{\mathrm{ab}} \\ \quad = mg\,(l-\varDelta l )(\cos\theta_0 - \cos\theta_1) \] 上式に与えられた近似式を適用すると, \[\varDelta E = mg(l-\varDelta l)(\cos \theta_0 -\cos \theta_1) \\ \quad \fallingdotseq mg(l-\varDelta l)\bigg(\bun{\theta_1{}^2}{2}-\bun{\theta_0{}^2}{2}\bigg) \cdots\cdots\maru{1} \] 一方,(1),(3)の結果より,\[W_g+W_{遠} = m g\cdot \varDelta l \cdot \bun{\theta_0{}^2}{2} + mg \cdot \theta_0{}^2 \cdot \varDelta l \\ \quad\quad\quad\quad\quad = \bun{3}{2}mg\cdot \varDelta l \cdot \theta_0{}^2 \cdots\cdots\maru{2} \] $\maru{1}$ 式, $\maru{2}$ 式 より, \[ \therefore \bun{1}{2}mg(l-\varDelta l)(\theta_1{}^2-\theta_0{}^2) = \bun{3}{2}mg\cdot\varDelta l \cdot\theta_0{}^2 \\ \therefore \theta_1{} = \underline{\kon{\bun{l+2\varDelta l}{l-\varDelta l}}\theta_0}\cdots\cdots\maru{3} \] (5) 次の半周期後の最大触れ角を $\Theta_1$ とすると,上記 $\maru{3}$ 式の $\theta_0$ を $\theta_1$ に置き換えればよいので,\[\Theta_1 = \kon{\bun{l+2\varDelta l}{l-\varDelta l}}\theta_1 \\ \quad = \bigg(\kon{\bun{l+2\varDelta l}{l-\varDelta l}}\bigg)^2\,\theta_0\] となる。このように,半周期ごとに振れ角は $\kon{\bun{l+2\varDelta l}{l-\varDelta l}}$ 倍になっていくので,$N$往復したときの振れ角 $\Theta_N$ は, \[\Theta_N = \bigg ( \kon{\bun{l+2\varDelta l}{l-\varDelta l}}\,{}\bigg )^{2N}\theta_0 =\underline{\bigg (\bun{l+2\varDelta l}{l-\varDelta l}\bigg )^N \theta_0}\]