◎ばね振り子の固定端を動かすと・・・
ばね振り子の固定端となっている側の端を揺すると,物体の運動はどのようなものになるでしょうか。
以下では,台Qを単振動させたときの物体Pの台上での動きについて考察してみることにします。
台Qとともに運動する観測者を想定し,この観測者が物体Pを見たときの運動について考えます。この場合,台Qの運動に伴う慣性力を考える必要があります(下図参照)。
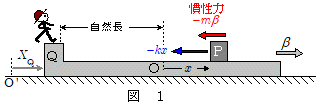
いま台Qを $X_\mathrm{Q} = A\,\cos \omega \,t $ のように単振動させたとします。このとき台の床に対する加速度 $\beta$ は\[\beta = \ddif{X_\mathrm{Q}}{t} = -\omega^2\,A\cos \omega\,t\]となるので,このときのばねの自然長からの伸びを $x$ ,ばね定数を $k$ とすると, 台に対する物体Pの運動方程式は,慣性力 $-\,m\,\beta$ を考慮して,\[\kern-1em m\,\ddif{x}{t} = -k\,x - \,m\,\beta \\ \kern2em = -k\,x + \,m\,\omega^2\,A\cos \omega\,t \]となります。
このように振動体が,復元力 $-k\,x$ のほかに,周期的に変化する力を受けて振動するとき,これを強制振動と言います。
◎強制振動
質量 $m$ ,ばね定数 $k$ のばね振り子に,周期変化する外力\[ F(t) = F_0\,\cos \omega \,t \quad\quad( F_0\,> 0\,)\]がはたらく場合,その運動方程式は,\[m\,\ddif{x}{t} = -k\,x + F_0\,\cos \omega \,t \\ \kern-1em \therefore m\,\ddif{x}{t} + k\,x = F_0\,\cos \omega \,t \quad\cdots\cdots\maru{1} \] この微分方程式の一般解は\[\kern-3em x = C\,\cos(\omega_0\,t +\phi ) + \bun{F_0}{m(\omega_0{}^2 - \omega^2)}\cos\,\omega\,t \quad\cdots\cdots\maru{2} \]となります。ただし $C$ , $\phi$ は積分定数であり,初期条件により定まります。また $\omega_0$ は, \[\omega_0 = \kon{\bun{k}{m}} \]です。この値 $\omega_0$ は,力 $F(t) $ の有無に関係なく,物体の質量 $m$ とばね定数 $k$ のみで決まる値であり,このばね振り子の固有角振動数と呼ばれています。
$\maru{2}$ 式の第1項\[ C\,\cos(\omega_0\,t +\phi ) \]は,ばねの弾性力のみで単振動しているときの一般解にあたります(『単振動』 $\maru{3}$ 式参照)。第2項は,周期的外力 $F(t)$ の作用によって新たに加わった項になります。
◎時刻 $\bbold{t=0}$ で $\bbold{x=0}$ , $\bbold{v = 0}$ の場合:
最も代表的な初期条件として,はじめ原点で静止していたばね振り子に力 $F(t)$ が作用し始めた場合について考えてみましょう。時刻 $t=0$ で $x=0$ , $v = 0$ とおいて,これより $C$ と $\phi$ が求まります。速度 $v$ は\[\kern-2em v = \dif{x}{t} \\ \kern-1.5em = -\,\omega_0\,C \,\sin(\omega_0\,t + \phi) - \bun{\omega\cdot F_0}{m(\omega_0{}^2 - \omega^2)}\sin \omega\,t \]なので, $x$ , $v$ に $t = 0$ を代入して,\[ \kern-1em x_{t=0} = C \cos(\phi) + \bun{F_0}{m(\omega_0{}^2 - \omega^2)} = 0 \\ \kern-1em v_{t=0} = -\,\omega_0 \,C\sin(\phi) + 0 = 0 \] 第2式より $\phi = 0$ ,これを第1式に代入して\[C = -\,\bun{F_0}{m(\omega_0{}^2 - \omega^2)} \] を得ます。以上より, $\maru{2}$ 式の $x$ は,\[\kern-2em x = -\,\bun{F_0}{m(\omega_0{}^2 - \omega^2)}\cos\omega_0\,t + \bun{F_0}{m(\omega_0{}^2 - \omega^2)}\cos \omega\, t \\ \kern -1.5em = \bun{F_0}{m(\omega_0{}^2 - \omega^2)}(\cos\omega\,t -\cos \omega_0\,t ) \\ \kern -1.5em = \bun{2F_0}{m(\omega_0{}^2 - \omega^2)}\cdot \sin\bigg(\bun{\omega_0 - \omega}{2}\,t \bigg) \cdot \sin\bigg(\bun{\omega_0 + \omega}{2}\,t \bigg) \quad\cdots\cdots\maru{3} \] ここで $\cos\alpha - \cos\beta = 2\sin\bigg(\bun{\beta - \alpha}{2}\bigg)\sin\bigg(\bun{\beta + \alpha}{2}\bigg)$ の関係を用いた。
上記 $\maru{3}$ 式より,特徴ある2つの振幅変化のパターンが導かれます。
(i) $\bbold{\omega \ne \omega_0 }$ だが,近い値の場合 → うなり
周期的外力 $F(t)$ の角振動数 $\omega$ がばね振り子の固有角振動数 $\omega_0$ にかなり近い値の場合,\[\bigg|\bun{\omega_0 - \omega}{2}\bigg| \ll \bun{\omega_0 + \omega}{2} \]と考えてよいので, $\sin\bigg(\bun{\omega_0 - \omega}{2}\,t \bigg)$ の項は $\sin\bigg(\bun{\omega_0 + \omega}{2}\,t \bigg)$ の項に比べてきわめてゆっくりした時間変化をすることになります。したがってこのときの $x$ は,あたかもゆっくりと時間変化する\[ \bigg|\, \bun{2F_0}{m(\omega_0{}^2 - \omega^2)} \sin\bigg(\bun{\omega_0 - \omega}{2} \,t \bigg) \,\bigg| \]を振幅とした角振動数 $\bun{\omega_0 + \omega}{2}$ の振動のように見えることになります。この様子をグラフにすると下図の青線ようになり,うなりを起こしているかのような時間変化をします。
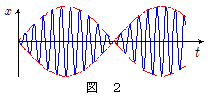
<参考> 本シミュレーションでは,『振動数比』を指定することで台の振動数が物体Pの固有振動数の『何倍であるか』を指定できます。この値を1に近い(1ではない!)値,「0.9」や「1.1」あたりの数値を選ぶことでこの「うなり」現象が見られます。
(ii) $\bbold{\omega} = \omega_0$ の場合 → 共振・共鳴
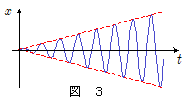
$\omega \rightarrow \omega_0$ の極限を考えます。とりあえず以下の近似により , \[ \sin\bigg(\bun{\omega_0 - \omega}{2}\,t \bigg) \kinji \bun{\omega_0 - \omega}{2}\,t \]とおくと, $\maru{3}$ 式は,\[\kern-2em x \kinji \bun{2F_0}{m(\omega_0{}^2 - \omega^2)} \cdot \bun{\omega_0 - \omega}{2}\,t \cdot \sin\bigg(\bun{\omega_0 + \omega}{2}\,t \bigg) \\ \kern-1.5em = \bun{F_0}{m (\omega_0 + \omega)}\,t \cdot \sin\bigg(\bun{\omega_0 + \omega}{2}\,t \bigg) \] ここで $\omega = \omega_0$ とおけば, \[ \kern-1.5em x = \bun{F_0}{2m \omega_0 }\,t \cdot \sin \omega_0\,t \quad\cdots\cdots\maru{4} \]となります。このとき振幅は\[\bigg|\bun{F_0}{2m \omega_0 }\,t \bigg| \]と表されますので,時間 $t$ に比例して限りなく増大していくことになります。これが共振,共鳴と呼ばれる状態です。
$x$ の時間変化の様子は,下図の青線のようになります。
(注。本シミュレーションでは,台の両端が壁になっているので,この範囲内での運動となります。)
◎抵抗力を伴う強制振動
ばね振り子が,周期的外力を受けながらさらに速度に比例する抵抗力も受ける場合,運動はさらに複雑になってきます。
周期的外力を $F = F_0 \cos\omega\,t$ ,抵抗力の比例定数を $c\,(\,>\,0\,)$ とすると,運動方程式は,\[m\,\ddif{x}{t} = -k\,x - c\,\dif{x}{t} + F_0\,\cos \omega \,t \\ \kern-1em \therefore m\,\ddif{x}{t} + c\,\dif{x}{t} + k\,x = F_0\,\cos \omega \,t \quad\cdots\cdots\maru{5} \]となります。この微分方程式の解は, $\maru{5}$ 式において周期的外力がない時,つまり 左辺 $=\,0$ なる微分方程式の一般解と,周期的外力があるときの $\maru{6}$ 式を満たす一つの特殊解 との和として表されます。
左辺 $=\,0$ とおいた式は,前項『 減衰振動』での $\maru{1}$ 式と同じであり,その解は,抵抗力の係数の大小によって3通りの式に場合分けされました(『減衰振動』の項で求めた $\maru{4}$ 式, $\maru{5}$ 式, $\maru{6}$ 式 を参照)。それらの3式はいずれも時間とともに $0$ に減衰していく関数でした。ここでは,これらをまとめて $u(t)$ と表すことにします。
一方,$\maru{5}$ 式を満たす一つの特殊解を $w(t)$ で表すとすれば,\[\mu = \bun{c}{2m},\quad \omega_0 = \kon{\bun{k}{m}}\]として, \[\kern-3em w(t) = \bun{F_0}{m\kon{(\omega_0{}^2 - \omega^2)^2 +4\mu^2\,\omega^2}}\,\cos(\omega\,t + \phi) \\ \kern15em \quad\cdots\cdots\maru{6} \\ ただし \quad \tan\phi = - \bun{2\mu\omega}{\omega_0{}^2 - \omega^2} \]のようになります。
したがって $\maru{5}$ の微分方程式を満たす一般解 $x$ は\[x = u(t) + w(t) \]ですが,減衰振動の項 $u(t)$ は時間とともに $0$ に漸近していくので,時間経過とともに特殊解の項 $w(t)$ ( $\maru{6}$ 式)だけが残ることになります。つまり十分時間が経つと,物体Pは,その固有振動数 $\omega_0$ ではなく,台の振動数 $\omega$ で振動することになります。また $w(t)$ ( $\maru{6}$ 式)から分かるように,たとえ $\omega = \omega_0$ の場合であっても,先の共振でみたような振幅が無限大に増大・・・・といった事にはなりません。これは,抵抗力がはたらかない強制振動の場合とは大きく異なる点です。さらに周期外力 $F(t)$ と $w(t)$ との間に位相差 $\phi$ を生じるので,台の振動とと物体の振動に時間的なずれが生じることを意味します。
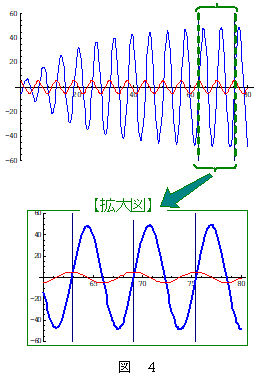
振動数比 $= 1.0$ 倍,抵抗係数 $c = 0.1$ あたりの数値を選ぶと,振幅が一定値になっていくこと,台の振動との間に位相差が生じることなどが確認できるでしょう。
図4は,上の値を前記の微分方程式 $\maru{5}$ 式に代入し,その近似解をもとにして $x$ の時間変化を数学ソフト Mathematica で描画したものです。青線が物体Pの,赤線が台Qのものです。図4の下の図は,振幅が一定した辺りの時間帯の拡大図で,物体の振動が台の振動より 1/4 周期分遅れている様子が分かります。