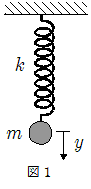◎1次元媒質を伝わる波のエネルギー
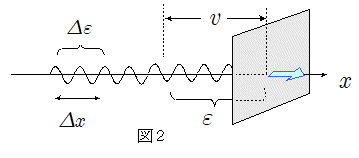
図2のように,$x$ 軸に沿って波を伝える1次元媒質(線密度は $\rho$ )があり,この媒質上を角振動数 $\omega$ ,振幅 $A$ の波が速さ $v$ で $x$ 軸の正方向に伝わっているとする。
このときこの媒質上各点における振動のエネルギーは上記で述べたように時刻,場所によらず一定であり,単位長あたりの振動エネルギーは,上記で求めた $\maru{1}$ 式における質量 $m$ をこの媒質の単位長あたりの質量,すなわち線密度 $\rho$ に置き換えたものに等しい。よって長さ $\varDelta x$ の部分に含まれている振動エネルギー $\varDelta \varepsilon$ は,\[\varDelta \varepsilon = \bun{1}{2}\rho \, \omega^2A^2\times\varDelta x \]と表される。
この媒質上を上記の振動が速さ $v$ で次々と移動していくのであるから,これに伴って振動エネルギーもこの媒質上を速さ $v$ で移動していくことになる。したがって,単位時間にこの媒質上の1点を通過していく振動のエネルギー $\varepsilon$ は,長さ $v$ の区間に含まれる エネルギーということになるので,上式の $\varDelta x$ を $v$ に置き換えたものとなり,\[\varepsilon = \bun{1}{2}\rho \, \omega^2A^2 \cdot v \]と表されることになる。
一般に,角振動数 $\omega=2\pi f$ ( $f$ :振動数),振幅 $A$ の波が速さ $v$ で伝わるとき,単位時間に運ばれる波のエネルギー(波の強さ) $I$ は, \[\quad\quad\quad \fbox{$ I \, \propto \,\rho \times \omega^2\times A^2\times v \quad\\ \quad\quad \propto \,\rho \times f^2 \times A^2 \times v $}\]の関係がある。この関係は,2次元,3次元媒質を伝わる波動についても成立する。