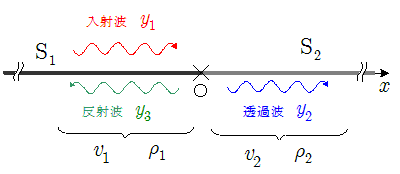
この場合,波が異なる媒質上を伝播していく条件として,次の2つが満たされていなくてはならない。
いずれも媒質の不連続点(この場合は $x=0$ の点)において,
1° 媒質の変位が2つの媒質の接続点($x=0$ の点)で連続していなくてはならない。(変位の連続性)
2° 媒質上のすべての点で,エネルギーの保存則が成立していなくてはならない。(エネルギーの保存則)
(エネルギー保存則の代わりに,変位の距離勾配(変位の傾き)の連続性を考えるのが普通だが,高校生にはエネルギーの保存則の方が理解しやすいと思われるので,ここではその立場で説明する。)
まず1°について考えよう。接続点($x=0$ )において,媒質 $\mathrm{S}_1$ 側の変位( $y_1(0\,,t)+y_3(0\,,t)$ )と $\mathrm{S}_2$ 側の変位( $y_2(0\,,t)$ )が常に等しいという式を立てる。$x=0$ の点でのそれぞれの波動による振動は,上の3式に $x=0$ を代入すればよいので, \[ \quad y_1(0\,,t)+y_3(0\,,t)=y_2(0\,,t) \\ \therefore A\sin\omega t+C\sin\omega t = B\sin\omega t \\ \therefore A+C = B \quad\cdots\cdots\maru{1} \] 次に,2°について考える。波動が単位時間に運ぶエネルギー量を,波の強さという。波の強さ $I$ は,次式で与えられる(「波のエネルギー」の項を参照)。 \[ I=\bun{1}{2}\times ( 媒質の密度 )\times ( 角振動数 )^2 \times ( 振幅 )^2 \times 伝播速度 \] 入射波,透過波,反射波の波の強さをぞれぞれ$I_1$,$I_2$,$I_3$とすると,$x=0$ の点に単位時間あたり$I_1$のエネルギーが入射し,その一部は透過波エネルギー $I_2$として透過し,残りのエネルギーは反射波エネルギー $I_3$として反射していくので,$x=0$ の点におけるエネルギー保存則は,\[ I_1=I_2+I_3 \\ \therefore \bun{1}{2}\rho_1 \omega^2 A^2 v_1=\bun{1}{2}\rho_2 \omega^2 B^2 v_2 + \bun{1}{2}\rho_1 \omega^2 C^2 v_1 \\ \therefore \rho_1 A^2 v_1=\rho_2 B^2 v_2 + \rho_1 C^2 v_1 \quad\cdots\cdots\maru{2} \] $\maru{1}$と$\maru{2}$をを連立させて,$B$, $C$ を$A$で表すと, \[\left \{ \begin{array}{rl} & \kern-1em B=0 \\ & \kern-1em C=-A \end{array} \right . \quad\cdots\cdots\maru{3}\quad or \left \{ \begin{array}{rl} & \kern-1em B=\bun{2\rho_1v_1}{\rho_1v_1+\rho_2v_2}A \\ & \kern-1em C=\bun{\rho_1v_1-\rho_2v_2}{\rho_1v_1+\rho_2v_2}A \end{array} \right . \quad\cdots\cdots\maru{4} \] $\maru{3}$ は透過波の振幅 $B$ が $0$ ということで,当初より透過波を否定している解になるのでこれは不適。よって $\maru{4}$ が $B$ , $C$ を与える式となる。
上記 $\maru{4}$ 式より,$\rho_1 v_1$,$\rho_2 v_2$ の大小にかかわらず $B>0$ であり, $y_2(0\,,t)$ は常に $y_1(0\,,t)$ と同符号,つまり接続点においては透過波はいかなる場合においても入射波と同位相(=位相のずれを生じない)ということになる。
これに対して,$C$ は$\rho_1 v_1$,$\rho_2 v_2$ の大小によって符号が変わる。正ならば $y_3(0\,,t)$ は $y_1(0\,,t)$ と同符号,つまり反射波の位相は入射波と同じだが,負ならば $y_3(0\,,t)$ は $y_1(0\,,t)$ と反対符号,つまり反射波の位相は入射波の位相と $\pi$ のずれを示すことになる。
以上をまとめると,以下のようになる。
・透過波はいかなる場合においても位相のずれを生じない。
\[\kern-3em ・反射波は,\left \{ \begin{array}{rl} & \kern-1em \rho_1v_1>\rho_2v_2 なら,C>0\\ & \kern-1em → 位相のずれなし(自由端反射) \\ & \kern-1em \rho_1v_1<\rho_2v_2 なら,C<0\\ & \kern-1em → \pi の位相のずれ(固定端反射) \end{array} \right . \]
◎弦を伝わる横波の場合:
弦を伝わる横波の速さ $v$ は,弦の張力を$S$,弦の線密度を $\rho$ とすると, \[v=\kon{\bun{S}{\rho}}\]という式で与えられる(質点列を伝わる横波モデル)。よって,\[ \rho v=\rho \kon{\bun{S}{\rho}\,}=\kon{\rho S\,}\,\propto \, \kon{\rho} \quad\cdots\cdots\maru{5}\]であるから,これを$\maru{4}$式に代入して式変形していくと(張力$S$は一定),\[ \left \{ \begin{array}{rl} & \kern-1em B=\bun{2\rho_1v_1}{\rho_1v_1+\rho_2v_2}A=\bun{2\kon{\rho_1}}{\kon{\rho_1}+\kon{\rho_2}}A\\ & \kern-1em C=\bun{\rho_1v_1-\rho_2v_2}{\rho_1v_1+\rho_2v_2}A=\bun{\kon{\rho_1}-\kon{\rho_2}}{\kon{\rho_1}+\kon{\rho_2}}A \end{array} \right . \quad \cdots\cdots\maru{6} \] また$\maru{5}$より,\[ v=\kon{\bun{S}{\rho}}\quad\therefore \rho=\bun{S}{v^2}\quad\therefore \rho v=\bun{S}{v} \] よって$\maru{6}$式に代わって,\[ \left \{ \begin{array}{rl} & \kern-1em B=\bun{2\rho_1v_1}{\rho_1v_1+\rho_2v_2}A =\bun{2\times \bun{S}{v_1}}{\bun{S}{v_1}+\bun{S}{v_2}}A =\bun{2v_2}{v_2+v_1}A \\ & \kern-1em C=\bun{\rho_1v_1-\rho_2v_2}{\rho_1v_1+\rho_2v_2}A = \bun{\bun{S}{v_1}-\bun{S}{v_2}}{\bun{S}{v_1}+\bun{S}{v_2}}A=\bun{v_2-v_1}{v_2+v_1}A \end{array} \right .\quad\cdots\cdots\maru{7} \] 本シミュレーションは,この $\maru{7}$ 式にしたって透過波,反射波の振幅を決定している。
以上より,弦の場合の反射波の位相は,
\[ \left . \begin{array}{rl} & \kern-1em \rho_1>\rho_2 \\ & \kern-1em v_1 < v_2 \end{array} \right \} \cdots\cdots 位相のずれなし\color{red}{(自由端反射)} \] \[ \left . \begin{array}{rl} & \kern-1em \rho_1 < \rho_2 \\ & \kern-1em v_1 > v_2 \end{array} \right \} \cdots\cdots \pi の位相のずれ\color{red}{(固定端反射)} \]
となる。◎音波(縦波)の場合:
音波は縦波である。
前述の $\maru{4}$ 式は,2つの媒質の接続点における変位の連続性とエネルギー保存則より導かれた式ゆえ, $\maru{4}$ 式は音波の場合にもそのまま適用できる。
空気中で, $\rho_1 \kinji 1.3\mathrm{kg/m^3} $, $v_1 \kinji 340\mathrm{m/s}$,
水中で, $\rho_2 \kinji 10^3\mathrm{kg/m^3} $, $v_2 \kinji 1.5\mathrm{km/s}$,
$\therefore \rho_1v_1<\rho_2 v_2$
となるので,$C<0$,つまり空気中から水面に向かって音波が入射する場合,反射波は固定端反射をすることになる。
【参考】気体中を伝わる音速は,気体の密度を$\rho$,圧力を$P$,比熱比を$\gamma$として, $v=\kon{\gamma\bun{P}{\rho}}$
固体中を伝わる音速は,個体の密度を$\rho$,ヤング率を$E$として, $v=\kon{\bun{E}{\rho}}$
という式で与えられる。
◎光波の場合:
光波の場合は,前記の議論をそのまま当てはめることはできないので,あくまでもその類推として理解しておいていただきたい。
光波は横波ゆえ,弦の説明で用いた $\maru{7}$ 式を当てはめて考えてみる。 $\maru{7}$ 式中での$v_1$ ,$v_2$ を媒質 $\mathrm{S_1}$ ,$\mathrm{S}_2$ 中での光速と考え,さらに媒質 $\mathrm{S_1}$ に対する媒質 $\mathrm{S}_2$ の屈折率として $n=\bun{v_1}{v_2}$ を定義すると, $\maru{7}$ 式は,\[ \left \{ \begin{array}{rl} & \kern-1em B = \bun{2v_2}{v_2+v_1}A = \bun{2}{1+\bun{v_1}{v_2}}A=\bun{2}{1+n}A \\ & \kern-1em C = \bun{v_2-v_1}{v_2+v_1}A = \bun{1-\bun{v_1}{v_2}}{1+\bun{v_1}{v_2}}A=\bun{1-n}{1+n}A \end{array} \right . \] このことから,屈折率$n$が $n<1$ ならば $C>0$ ,つまり反射光波は入射光波と同位相, $n>1$ ならば $C<0$ ,つまり反射光波は入射光波に対して位相が $\pi$ ずれる。これに対して, $n$ の値によらず $B>0$ であるから,透過光波の位相はずれることはない。 $n<1$ の場合を光学的に疎,$n>1$ の場合を光学的に密という。
以上をまとめると,
\[ \left \{ \begin{array}{rl} & \kern-1em 屈折率が 大→小 への入射 \cdots\cdots 位相のずれなし\color{red}{(自由端反射)}\\ & \kern-1em 屈折率が 小→大 への入射 \cdots\cdots \pi のずれ\color{red}{固定端反射)}\\ & \kern-1em 透過波の位相はずれない。 \end{array} \right . \]
上記のことは,光波を含む横波一般について成立する。戻る