☆ばねに連結された小球群列を伝わる縦波モデル：

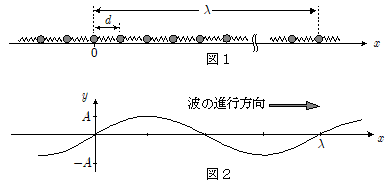
　図１のように，質量 $m$ の多数の小球が自然長 $d$ ，ばね定数 $k$ のばねで連結されて $x$ 軸上に並んでいるとする。これを，小球群列と呼ぶこととする。
　この小球群列の一方の端（$x$ 軸の負の方向側の端）の小球に周期 $T$ の振動をばね方向に与え続けると，この振動は次々と小球群列を $x$ 軸の正の向きに伝わっていく。この様子は，媒質上を伝わっていく縦波と似ている。
　以下，この小球群列上を伝わっていく振動を，波長 $\lambda$ ，周期 $T$ の縦波と考えて，その振動（波動）が伝わっていく速さ $v$ を求めてみよう。ただし，波長 $\lambda$ はばねの自然長 $d$ や小球の振動振幅 $A$ に比べて十分に大きい（ $　\lambda \gg d > A$ ）ものとし，小球の大きさ，ばねの質量は無視する。
　図２は，時刻 $t=0$ における小球の変位 $y$ （波がないとき（平衡時）からのずれ）を，各小球の本来の $x$ 座標に対して描いたものである。ただし $x$ 軸正方向の変位を $y$ の正とし，$d\ll \lambda$ であることから各小球の変位を連続的な曲線で結んで示してある。

☆力学的考察：
　

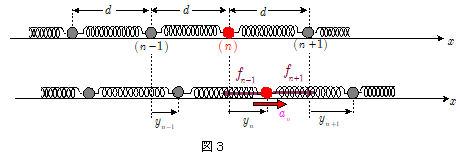
　図３の赤色で示した小球を $n$ 番目，その左側の小球を $(n-1)$ 番目，右側の小球を $(n+1)$ 番目の小球と名付けよう。
　いまある時刻において，$n$ 番目， $(n-1)$ 番目， $(n+1)$ 番目の小球の平衡位置からの変位がそれぞれ $y_{n}$ ， $y_{n-1}$ ， $y_{n+1}$ であり，$n$ 番目の小球の加速度が $a_{n}$ であったとする。ただし $a_{n}$ は， $x$ 軸の正方向を正とする。
　このとき $(n-1)$ 番目 と $n$ 番目の小球間のばねの伸びは $(y_n - y_{n-1})$ ， $n$ 番目 と $(n+1)$ 番目小球間のばねの伸びは $(y_{n+1} - y_n)$ であるから，$n$ 番目小球が $(n-1)$ 番目，$(n+1)$ 番目の小球から受ける力は，それぞれ図３で示した向きを正として，\[f_{n-1} = k(y_n - y_{n-1} ) \\ f_{n+1} = k(y_{n+1} - y_n ) \]である。よって$n$ 番目の小球の運動方程式は\[m\, a_n = -f_{n-1} + f_{n+1} \\ \quad = - k(y_n - y_{n-1} ) + k(y_{n+1} - y_n ) \\ \quad = - k \big(2 y_n - y_{n-1} - y_{n+1} \big) \cdots\cdots\maru{1}\] 　この小球群列を波長 $\lambda$ ，周期 $T$ の振動が速さ $v$ で伝わってきていると考えているのであるから，すべての小球は周期 $T$ で単振動していることになる。いま， $n$ 番目小球の変位 $y_{n}$ が時刻 $t$ の関数として，\[y_n = A\, \sin\bigg( \bun{2\pi}{T}t + \delta \bigg) \cdots\cdots\maru{2} \]であるとする。ここで $A\,\,(\,\lt d\,)$ は振幅， $\delta$ はある定数とする。このとき $(n-1)$ 番目， $(n+1)$ 番目の小球の変位 $y_{n-1}$ ， $y_{n+1}$ は，波が距離 $d$ だけ伝わるのに $\bun{d}{v}$ の時間差を生じることを考慮して，\[y_{n-1} = A \, \sin\bigg\{ \bun{2\pi}{T}\bigg(t + \bun{d}{v}\bigg)+ \delta \bigg\} \cdots\cdots\maru{3} \\ y_{n+1} = A \, \sin\bigg\{ \bun{2\pi}{T}\bigg(t - \bun{d}{v}\bigg)+ \delta\bigg\} \cdots\cdots\maru{4} \]　 $\maru{2} \thicksim \maru{4}$ を $\maru{1}$ に代入していく。 $ \sin\alpha + \sin\beta = 2\cos\bun{\alpha-\beta}{2} \cdot \sin\bun{\alpha+\beta}{2}$ の公式を利用して，\[\quad y_{n-1} + y_{n+1} = \, \maru{3} \, + \, \maru{4} \\ \quad\quad\quad\quad\quad\quad = 2A\, \cos\bigg(\bun{2\pi \,d}{T\, v}\bigg) \times \sin\bigg(\bun{2\pi}{T}t +\delta \bigg) \\ \quad\quad\quad\quad\quad\quad = 2 \cos \bigg( \bun{2\pi \, d}{T\, v} \bigg) \times y_n \\ \therefore m\,a_n = - k \big(2 y_n - y_{n-1} - y_{n+1} \big) \\ \quad\quad\quad = -2k \bigg\{1 - \cos\bigg(\bun{2\pi\,d}{T \, v}\bigg)\bigg\}\times y_n \cdots\cdots\maru{5}\]　よって\[\underline{\omega^2 = \bun{2k}{m}\bigg\{1 - \cos\bigg(\bun{2\pi\,d}{T \, v}\bigg)\bigg\} } \cdots\cdots\maru{6} \]とおくと，上記 $\maru{5}$ 式は\[ m\,a_n = -m\, \omega^2\,\cdot y_n \\ \therefore a_n = - \omega^2 \,\cdot y_n \]となり， $n$ 番目小球に対する単振動の運動方程式が得られる。ここで $\omega = \bun{2\pi}{T}$ であるから， $\maru{6}$ 式は，\[\bigg(\bun{2\pi}{T}\bigg)^2 = \bun{2k}{m}\bigg\{1 - \cos\bigg(\bun{2\pi\,d}{T \, v}\bigg)\bigg\} \] 　ここで $\cos\theta = 1 - 2\sin^2\bun{\theta}{2}$ の公式を利用して，\[\bigg(\bun{2\pi}{T}\bigg)^2 = \bun{2k}{m}\bigg\{1 - \cos\bigg(\bun{2\pi\,d}{T \, v}\bigg)\bigg\} \\ \quad\quad\quad\quad = \bun{2k}{m}\bigg[ 1 - \bigg\{ 1 - 2\sin^2\bigg(\bun{2\pi\,d}{2T \, v}\bigg) \bigg\} \bigg] \\ \quad\quad\quad\quad = \bun{4k}{m}\sin^2\bigg( \bun{\pi\,d}{T \, v }\bigg) \\ \therefore \bun{2\pi}{T} = 2\kon{\bun{k}{m}}\sin\bigg(\bun{\pi\,d}{T \, v }\bigg) \] 　また，波の速さと周期，波長の基本式より　 $T \, v = \lambda$　であるから，上式より $T$ を消去すると，\[\bun{\pi\,v}{\lambda} = \kon{\bun{k}{m}}\sin\bigg(\bun{\pi\,d}{\lambda}\bigg) \] 　小球間隔 $d$ は十分に小さく$d\ll \lambda$ であるという前提であるから， $\bun{\pi\, d}{\lambda} \ll 1$ である。よって $|\theta| \ll 1$ であるときの次近似式 $\sin\theta \kinji \theta$ を使うと，\[ \bun{\pi\,v}{\lambda} = \kon{\bun{k}{m}}\sin\bigg(\bun{\pi\,d}{\lambda}\bigg) \\ \quad\quad \kinji \kon{\bun{k}{m}}\times \bun{\pi \, d}{\lambda} \\ \therefore \color{blue}{\fbox{$\quad v=\kon{\bun{k}{m}}\, d \quad $}} \]　これが，この場合の小球群列を縦振動（縦波）が伝わっていく速さとなる。