2つ以上の波が重なって,強め合ったり弱めあったりする場所ができることを「波の干渉」といいます。
弦のような1次元媒質にできる定常波も,互いに逆向きに進む波が干渉している結果ということができます(定常波を参照)。
本シミュレーションで取り上げている2つの点波源から発せられ円形状に広がっていく波の干渉模様は,教科書等でよく見かけると思います。
参考までに,図1は3つの点波源から広がる円形波の干渉模様を表します。「波のシミュレーション」において,点波源を3個配置して作成したものです。波源の数はいくつでも可能ですので試してみてください(4波源の例は ココをクリック )。

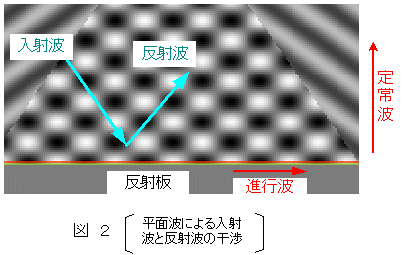
また図2は,反射板に平面波が入射したとき,入射波と反射波とによってできる干渉縞で,反射板に沿った方向には進行波ができ,反射板に垂直な方向には振幅が周期的に変化しています。すなわち,反射板に垂直な方向には定常波ができていることになります。「平面波の屈折と反射」のシミュレーションで確認してみてください。
◎円形波の干渉-腹線と節線
下図は,本シミュレーションで作成した円形波の例です(不鮮明,かつ見にくい図ですが・・・)。 $x$ 軸上に点波源 $\mathrm{S}_1$ , $\mathrm{S}_2$ があり,薄青色の円は点波源 $\mathrm{S}_1$ から,橙色の円は $\mathrm{S}_2$ から出た円形波の,それぞれ1波長ごとの「山」を表しているとします。
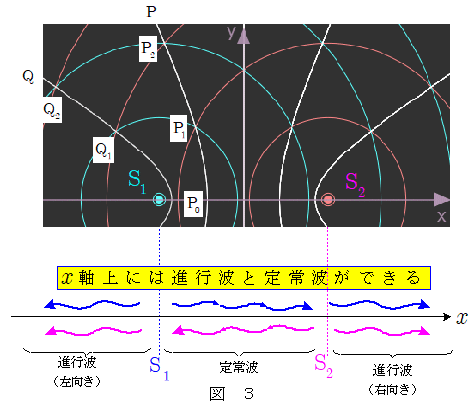
このとき各円形波の「山」波面の交点は,それぞれある曲線上または直線上にあります。
例えば一つの曲線P上の $\mathrm{P}_2$ ~ $\mathrm{P}_0$ に注目してみてください。点 $\mathrm{P}_2$ は $\mathrm{S}_1$ からの円形波2波長分, $\mathrm{S}_2$ からは3波長分の位置にあり, $\mathrm{S}_1$ , $\mathrm{S}_2$ からこの点 $\mathrm{P}_2$ までの距離の差は1波長分になります。点 $\mathrm{P}_1$ に注目すると,この点は $\mathrm{S}_1$ から1波長分, $\mathrm{S}_2$ から2波長分の位置にあり,やはり $\mathrm{S}_1$ , $\mathrm{S}_2$ からの距離の差は1波長分になります。点 $\mathrm{P}_0$ は $x$ 軸上にありますが, $\mathrm{S}_1$ から $0.5$ 波長分, $\mathrm{S}_2$ から $1.5$ 波長分の位置で,やはり1波長分の距離差があります。同様に曲線Q上の点 $\mathrm{Q}_2$ , $\mathrm{Q}_1$ では, $\mathrm{S}_1$ , $\mathrm{S}_1$ からの距離差は2波長分になります。
このように2つの波源から出た波の山と山の交点(あるいは谷と谷の交点)は2波源からの距離の差が一定となる曲線または直線に沿って移動していくことがわかります。2点からの距離の差が一定となる曲線は双曲線または直線です。波の山・山の交点もしくは谷・谷では振幅の大きな波ができていることになりますが,これらの交点を結ぶ線を「腹線」と呼ぶことにすれば,「腹線」は双曲線または直線ということになります。同様に,山と谷の交点では変位が打ち消しあって波は消えていることになりますが,このような点を結ぶ線(「節線」という)も双曲線もしくは直線になります。つまり,腹線も節線も双曲線もしくは直線をなすことになります。
ところで $x$ 軸上では,点波源 $\mathrm{S}_1$ , $\mathrm{S}_2$ から出た波はそれぞれ $x$ 軸の正,負の両方向に進んでいきますが, $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間ではそれぞれの波が互いに逆向きに進んでおり,その外側では2つの波はともに同じ向きに進むことになります。2つの同波長の波が互いに逆向きに進むときその合成波は定常波となり,同じ向きに進むときはその合成波は進行波となります。そして定常波では腹と節ができます。前述の点 $\mathrm{P}_0$ は腹線と $x$ 軸との交点であり, $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間にできている定常波の腹の位置にあたります。すなわち,
腹線は2つの点波源間にできる定常波の腹の位置を通り,節線は2つの点波源間にできる定常波の節の位置を通ることになります。したがって腹線や節線が何本できるかを知るには,2つの点波源間にできる定常波の腹,節の数を調べればよいことになります。
なお図3よりわかるように,$x$ 軸上の $\mathrm{S}_1$ ~ $\mathrm{S}_2$ の両外側にできる進行波の振幅については, $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間にできている定常波の両端の点 $\mathrm{S}_1$ , $\mathrm{S}_2$ の振動振幅がいくらになるかによって変化します。したがって例えば $\mathrm{S}_1$ , $\mathrm{S}_2$ が定常波の腹の位置になるとすれば, $\mathrm{S}_1$ ~ $\mathrm{S}_2$ の両外側にできる進行波の振幅も最大となり, 点 $\mathrm{S}_1$ より負の側, $\mathrm{S}_2$ より正の側の $x$ 軸上には腹線ができることになります。また逆に $\mathrm{S}_1$ , $\mathrm{S}_2$ が定常波の節の位置になるとすれば,上記の $x$ 軸上の範囲には節線ができることになります。
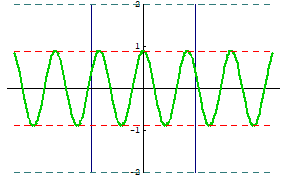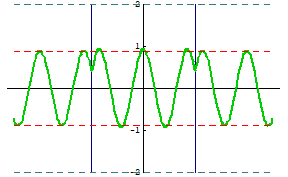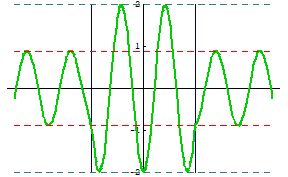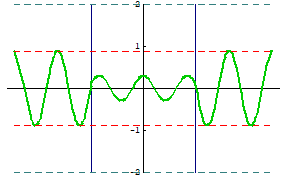
下のアニメは,図3において $x$ 軸上にできる波の一例です。 $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間には定常波が,その両サイドには進行波ができていることがわかります。詳細は次の詳解を参照してください。
シミュレーションへ戻る
詳解に進む