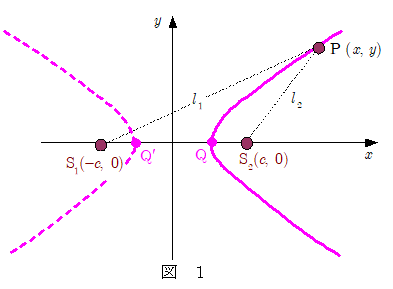
前頁の 概要で述べたように, $\mathrm{S}_1$, $\mathrm{S}_2$ からの波によって腹線や節線ができますが,これらは双曲線もしくは直線をなします。そしてこれらの双曲線もしくは直線は, $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間の $x$ 軸上にできる定常波の腹もしくは節の位置を通るということでした。
腹線や節線の双曲線は $\maru{1}$ 式のように表されますが,この式に含まれる定数 $c$ は2波源の $x$ 座標の値であり,既知の値です。
一方定数 $a$ は双曲線の $x$ 軸上の切片の $x$ 座標を与える値であり,したがって腹線や節線を表す双曲線に関する $a$ の値は $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間の $x$ 軸上にできる定常波の腹もしくは節の $x$ 座標にほかなりません。
以下,$x$ 軸上にできる定常波の腹,節の $x$ 座標がどのように表されるかについて考えていきましょう。
2点 $\mathrm{S}_1 \,\,( -c, \,\,0 )$ , $\mathrm{S}_2 \,\,( c,\,\, 0 )$ から振動数 $f$ ,波長 $\lambda$ ,振幅 $A$ の波が発せられているとします。ただし, $\mathrm{S}_2 $ の振動は $\mathrm{S}_1 $ の振動に対して位相差 $\delta$ だけ遅れて振動しているとします。
いま上図1の点 $\mathrm{P} \,\,( x, \,\,y )$ における $\mathrm{S}_1 $, $\mathrm{S}_2 $ からの波の時刻 $t$ における変位 $\phi_1$, $\phi_2$ が, $\mathrm{S}_1 $, $\mathrm{S}_2 $ から点Pまでの距離を $l_1$, $l_2$ として,\[\phi_1 = A \cos \bigg\{ 2 \pi ( f t - \bun{l_1}{\lambda} ) \bigg \} \\ \phi_2 = A \cos \bigg \{(2 \pi ( f t - \bun{l_2}{\lambda} ) - \delta \bigg\} \] と表されるとすれば,点 $\mathrm{P}$ の全変位 $\varPhi$ は,\[\begin{eqnarray*} \cos \alpha + \cos \beta &=& 2 \cos \bun{\alpha - \beta}{2} \times \cos \bun{\alpha + \beta}{2} \\ &=& 2 \cos \bun{\beta - \alpha}{2} \times \cos \bun{\alpha + \beta}{2} \end{eqnarray*} \]の関係式を用いて, \[\kern-1em \varPhi = \phi_1 + \phi_2 \\ = 2A \cos \bigg \{ \bun{\pi}{\lambda}(l_1 - l_2 ) - \bun{\delta}{2} \bigg \} \times \cos \bigg \{2 \pi \bigg ( f t - \bun{l_1 + l_2 }{2\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \cdots\cdots\maru{2} \]
ここで,\[l_1 = \kon{( x + c )^2 + y^2} \\ l_2 = \kon{( x - c )^2 + y^2} \]ですので, $x$ 軸上であればこれらに $y = 0$ とおいていけばよいのですが,根号を外すときに符号に注意が必要です。
(i) $\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間では $-c \le x \le c$ ですから,\[l_1 = x + c \\ l_2 = -(x - c) \\ \kern-1em \therefore l_1 - l_2 = 2 x \\ \, l_1 + l_2 = 2 c \\ \kern-1em \therefore \varPhi = 2A \cos \bigg \{ \bun{\pi}{\lambda}(l_1 - l_2 ) - \bun{\delta}{2} \bigg \} \times \cos \bigg \{2 \pi \bigg ( f t - \bun{l_1 + l_2 }{2\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \\ \kern1em = 2A \cos \bigg (\bun{2\pi}{\lambda} x - \bun{\delta}{2} \bigg ) \times \cos \bigg \{2 \pi \bigg ( f t - \bun{c }{\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \] 上式の右辺第2項は時間 $t$ を含んでいるが座標 $x$ を含んでいないので,この項は各点が振動数 $f$ で振動しているよ・・・ということを表しています。一方第1項は時間 $t$ を含まず,座標 $x$ を含んでいます。つまり座標 $x$ の点の振動の大きさはこの第1項によって決まることを意味し,その絶対値が振幅を表すことになります。
振幅を $B$ とすれば,\[B = 2A \bigg |\cos \bigg (\bun{2\pi}{\lambda} x - \bun{\delta}{2} \bigg ) \bigg | \cdots\cdots\maru{3}\] このように$\mathrm{S}_1$ ~ $\mathrm{S}_2$ 区間では各点の振動振幅は位置 $x$ によって定まっていることなり,これがこの区間の $x$ 軸上に定常波ができている・・・ということなのです。
◎腹の位置では $B = 2A$ であるから, $m = 0,\, \pm 1, \, \pm 2, \, \cdots\cdots $ として,\[ 2A \bigg |\cos \bigg (\bun{2\pi}{\lambda} x - \bun{\delta}{2} \bigg ) \bigg | = 2A \\ \kern-1em \therefore \bun{2\pi}{\lambda} x - \bun{\delta}{2} = m \,\pi \\ \kern-1em \therefore \color{red}{x = \bigg ( m + \bun{\delta}{2 \pi} \bigg ) \cdot \bun{\lambda}{2} \cdots\cdots 腹の x座標} \] ◎節の位置では $B = 0$ ですから,\[ 2A \bigg |\cos \bigg (\bun{2\pi}{\lambda} x - \bun{\delta}{2} \bigg ) \bigg | = 0 \\ \kern-1em \therefore \bun{2\pi}{\lambda} x - \bun{\delta}{2} = \bigg (m + \bun{1}{2}\bigg ) \,\pi \\ \kern-1em \therefore \color{red}{x = \bigg ( m + \bun{1}{2} + \bun{\delta}{2 \pi} \bigg ) \cdot \bun{\lambda}{2} \cdots\cdots 節の x座標} \] (ii) $\mathrm{S}_1$ より左方の $x$ 軸上では $x \le -c$ なので,,\[l_1 = -( x + c ) \\ l_2 = -(x - c) \\ \kern-1em \therefore l_1 - l_2 = -2 c \\ \, l_1 + l_2 = -2 x \\ \kern-1em \therefore \varPhi = 2A \cos \bigg \{ \bun{\pi}{\lambda}(l_1 - l_2 ) - \bun{\delta}{2} \bigg \} \times \cos \bigg \{2 \pi \bigg ( f t - \bun{l_1 + l_2 }{2\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \\ \kern1em = 2A \cos \bigg (- \bun{2\pi}{\lambda} c - \bun{\delta}{2} \bigg ) \times \cos \bigg \{2 \pi \bigg ( f t + \bun{x }{\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \] 上式第2項より, $\mathrm{S}_1$ より左方の $x$ 軸上では $-x$ 方向に進む進行波を生じ,その振幅は上式第1項の絶対値で与えられますが,その値は先に求めた$\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間にできる定常波の振幅を与える $\maru{3}$ 式に $x = -c$ を代入したものと同じになります。つまり,$\mathrm{S}_1$ より左方の $x$ 軸上にできる進行波の振幅は,$\mathrm{S}_1$ ~ $\mathrm{S}_2$ 間にできる定常波の左端の振幅と同じだということになります。
(iii) $\mathrm{S}_2$ より右方の $x$ 軸上では $c \le x$ であることを考慮して同様に考えていくと,\[\varPhi = 2A \cos \bigg \{ \bun{\pi}{\lambda}(l_1 - l_2 ) - \bun{\delta}{2} \bigg \} \times \cos \bigg \{2 \pi \bigg ( f t - \bun{l_1 + l_2 }{2\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \\ \kern1em = 2A \cos \bigg ( \bun{2\pi}{\lambda} c - \bun{\delta}{2} \bigg ) \times \cos \bigg \{2 \pi \bigg ( f t - \bun{x }{\lambda} \bigg ) - \bun{\delta}{2} \bigg \} \] これより $\mathrm{S}_2$ より右方の $x$ 軸上では $+ x$ 方向に進む進行波を生じ,その振幅は前記 $\maru{3}$ 式に $x = c$ を代入したものと同じになることがわかります。
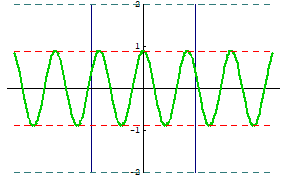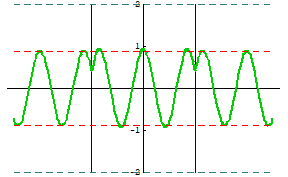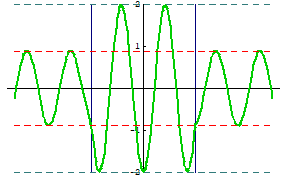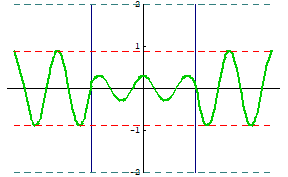
下のアニメは, $\lambda = 0.85 c$ , $\delta = 0$ , $A = 1$ の例です。
進行波の振動振幅 $B$ は,前記 $\maru{3}$ 式に $\lambda$ ,$\delta$ , $A$ の値,および $x = -c$ または $x = c$ を代入して,\[B = 2 \cos\bigg(\bun{6 \pi}{17} \bigg ) \kinji 0.89 \] となります。
シミュレーションへ戻る
概 要 に戻る