�x�N�g���@�s��@1���ϊ��@���b�i�I���W�i���ڂ₫�j
����͖^�������Z�ɓ��e�����l�^�ł����A�z�[���y�[�W�S���̐搶����ւ����悤�ŁA���������N����Ă��܂���B
�ꎟ�ϊ��@���̃y�[�W
��]���āA2���Ȑ��ނ��Ă݂�@����͂�����̃����N��
�P���ϊ��Ɠ��ꑊ�Θ_�ւ����܂�
http://www.ne.jp/asahi/imaimai/homepage/index�ɖ߂�
�O�i
���Z�łͽ�װ�ρi���ρj�����ł��邪�A�s��̐ς͓��ς��������߂�b�ł͂���B�������A�s�ƂȂ����ِρi�O�ρj�̂ق����W������B![]()
���ςƊO�ς́A���f�����g�����ē���ꂽ�u�S�����̐ς̉��Z���`�����v�Ƃ��납��̔h���ł���B
a��b�f���Ƃ��āA���炽�� j �Ƃ��������P�ʂ����@a�{bj�@�@�Ȃ�Ă̂�z������B
�@a �{ bj�@�@���A���A���A�������Ƃ��ā@a����+��i b=��+��i�@�@�ő�����Ă݂��
���{��i �{��j�{��ij �@ ����, i��j���|����Ƃǂ����H�@i�Ej=k�@�@ �Ȃ�ƐV�����܂��u�����P�� k �v�@���Ƃ����B�@���Ȃ킿4�������B
=���{��i �{��j�{��k�@�@�@�����P�ʂ��@i,j,k��3��������
�i�����4�������W���ɂ��āA�V���ȋ����P�ʂ��P�lj������8�����Ɋg������܂��j
�������u�̊W�́H
�E���������̓������̓��m�������� i,j,k��2�悷���-1�ɂȂ�
�E���������̈Ⴄ���̓��m��������ƁA�����ЂƂ̐����ɂȂ��@ij=k, jk=i , ki=j �@�����@���͐��藧�����A�����}�C�i�X�@
�����R�������R�����x�N�g���Ɏg����悤�ɂȂ����B
�������m�̊|���Z�̕�����i,j,k�̕������������x�N�g���Ƒz�肵�ĂX����\�ɂ��Ă݂���A�u�O�ρv�|�u���ρv�Ȃ̂ł���B
|
���~�� |
b1i |
b2j |
b3k |
|---|---|---|---|
|
a1i |
-a1b1 |
a1b2k |
-a1b3j |
|
a2j |
-a2b1k |
-a2b2 |
a2b3i |
|
a3k |
a3b1j |
-a3b2i |
-a3b3 |
�R�̋����̐����́A3�����ɂ�����R�̒P�ʃx�N�g�����m�̓��ς�O�ς̌��ɂȂ����̂ł���B
���f���i2�����j�A4�����̍s��\���@����͂�����̃����N��
��ق̓��ρE�O�ςƍs��̐�
���ρF
�Q�̐��̕������Ⴄ�i�������̌����������łȂ��j�����m�������̊|���Z�݂������v�Z
�ǂ������ɐ������̒�K�����킹�邱�Ƃɂ��āA����̌����̉���Ȃ����͂��̐������֎ˉe���Ƃ�A����ŕ��ʂ̎����̊|���Z������̂ł���B
�x�N�g���̌�����90�x�ȏ�J���ƁA�������قȂ鐔�̊|���Z�ɂȂ蕉�ɂȂ�B
�O�ρF
�����������Ă���ƌ����Ă��Ȃ��B90�x�ɊJ�����Ƃ�����Ԍ��ʂ�����B
�Q�̃x�N�g�����m�ł��镽�ʂɑ��Ė@���x�N�g���ł���B���̑傫���͂Q�̃x�N�g���ł��镽�s�l�ӌ`�̑傫���i�E�˂��̌����j�����ɂ��Ă���B
���ς�O�ς̐������݂�ɂ́A�P����قɕ����A�㐔�̊|���Z�̂悤�Ɉ����̂���̎肾�ˁB
�i�ꎟ�����́A�܂��A�e�v�f�̃X�J���[�{�������̘̂a�Ƃ����`���j�P�ʃx�N�g���ɕ��������Ƃ��̌W�����x�N�g���̐����\���ł����B

�R���~�R���@�W�J�ɂ���āA�X�̒P�ʃx�N�g�����Z�̍����o�Ă���B�P�ʃx�N�g���̓��ρE�O�ς̒P���Ȍv�Z���g����B
�X�ʂ�̑g�����\�ɂ��Č���ƁA���ς́u�����������m�̐ρv�̑g�ݍ��킹�̂݁A�O�ς͓����������m�̐ς̍��͂Ȃ��B
|
����� |
b1ex |
b2ey |
b3ez |
|---|---|---|---|
|
a1ex |
a1b1 |
�O |
�O |
|
a2ey |
�O |
a2b2 |
�O |
|
a3ez |
�O |
�O |
a3b3 |
|
���~�� |
b1ex |
b2ey |
b3ez |
|---|---|---|---|
|
a1ex |
�O |
a1b2ez |
-a1b3ey |
|
a2ey |
-a2b1ez |
�O |
a2b3ex |
|
a3ez |
a3b1ey |
-a3b2ex |
�O |
| ���� | �O�� | |
| �ǂ�ȗʂȂ� | �X�J���[ | �x�N�g���@�i3�����ȏ�łȂ��Ɛ������Ȃ��j |
| �����@�� | ���E���@���@���E�������� | ���������Ɂi���������j |
| �傫�� | |a||b|cos���@�@�@�x�N�g�����m�̂Ȃ��p�� ����̃x�N�g���ɐ����������킹�Ċ|���Z�������ʂł���B |
|a||b|sin���@�@�x�N�g�����m�̂Ȃ��p�� ����͂Q�̃x�N�g���ł��镽�s�l�ӌ`�̖ʐςł���B |
| �����Ȑ����͌����ė��Ȃ��B �Ⴆ�A �d���͗͂̐����̕ψʂ��y�ڂ����������������ʂ͂Ȃ��B�d���͗͂̃x�N�g���ƕψʃx�N�g���̓��ς��o�H�ɉ����ĐώZ�����`�ƂȂ�B |
���s�Ȑ����͌����ė��Ȃ��B �Ⴆ�A ���[�����c�͂́A�דd���q�̑��x�x�N�g���̎����ɑ��鉔���Ȑ������������Ă��Ȃ��B��l�Ȏ������ł̂点��^���Ƃ́A�~�^�����Ȃ�����A�����ɕ��s�ȑ��x���������邩��N���邱�Ƃł��� |
|
 |
2�����̏ꍇ�͂Q�̃x�N�g���̖@�������̃x�N�g���͒�`�ł��Ȃ��̂ŁA�������Ȃ��B �R�����ł������ʏ�̃x�N�g���̊O�ς��Ƃ�ƁAx,y�̗v�f�łł�����x�N�g���łł����s��̍s�̒l���������ƂȂ�B �Q�������s�͂Q�̂Q�����̗�x�N�g���ł��������s�l�ӌ`�̑傫�������Ă���B �R�̃x�N�g�����R�����Ō����ꍇ�A ���s�Z�ʑ̂̑傫���ƊW������̂́A�Q�̃x�N�g���ŊO�ς��Ƃ�A����Ǝc��̃x�N�g���Ɠ��ς��Ƃ����X�J���[�l�ł���B ����́A�R�̂R������x�N�g���łł����R�������s��̍s�Ɠ����傫���ł���B |
�X�J���[3�d��
1) �R�̃x�N�g���̂����Q��I�ъO�ρi�x�N�g���j�����߂�B
2) ����Ǝc��̃x�N�g���Ƃ̓��ς����߂�
�Ⴆ��,�@3�x�N�g��a,b,c�Łu���~���Ƃ�����فv�Ɓu��ق��v�̓��ς̌`���X�J���[�R�d�ςƂ����B
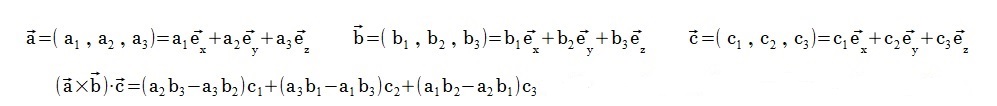
�]���q�W�J�ƃX�J���[�R�d��
��̗�Ƃ��ā@�O�ρ@���~���@�ŏ��̂��������Ƃ肠���Ă݂悤���B
���L�̂悤�ɗ���ق��A���A�����R��Ȃ�ׂāA3�~3�s����������Ƃ��i�Y�����̂P�C�Q�C�R���e�x�N�g��x,y,z�����ɑΉ����܂��j
|
a1 |
b1 |
c1 |
|---|---|---|
|
a2 |
b2 |
c2 |
|
a3 |
b3 |
c3 |
���~���̂����� (a2b3-a3b2)���A��L�R�~�R�s���c1�̏������Ă���s�Ɨ����菜���������s��Q�~�Q�s���̍s��
�ŁAc1���]���q�Ƃ����B�@y,z�����ɂ��Ă�c2,c3�̗]���q��������B
�����Am�sn��ڂ�m+n=��Ȃ�}�C�i�X��t����B�@3�s2��ڂȂ�@3+2=5�Ȃ̂Ń}�C�i�X�B
�i���~���j�E�� = (a2b3-a3b2)c1+(a3b1-a1b3)c2+(a1b2-a2b1)c3
��L�E�ӂ̂��Ƃ��A3��ځi���Ȃ킿�x�N�g��C�̐����j�łR���R�s��]���q�W�J�����Ƃ����B
�]���q�W�J�Ƃ́A����s����̐����ɒ��ځi3��ځj���A����ȊO�̗]���q�����i���̏ꍇ2�~2�s��3�ʂ�j�̍s��1����������B
�u�]���q�����łł����x�N�g���v�Ɓu��ق��v�Ƃ̓��ρ@�ƌ����Ă������B
����ɂ��s�̎�����3������2���̍s�ɉ��������`�ɓW�J�ł����i��ʉ��ł͎������������j�Ƃ�����ŁA��w�̐��`�㐔�ŏo�Ă�����̂��B
1��ڃx�N�g��a�A2��ڃx�N�g��b�ŗ]���q�W�J���Ă������s�ɂȂ�
�i���~���j�E���@ 1���a�x�N�g���v�f�̗]���q�W�J�ɑ���
�i���~���j�E���@ 2��ڂ��x�N�g���v�f�̗]���q�W�J�ɑ���
�ǂ̓W�J�����ʂ��O���Ă݂�Γ���
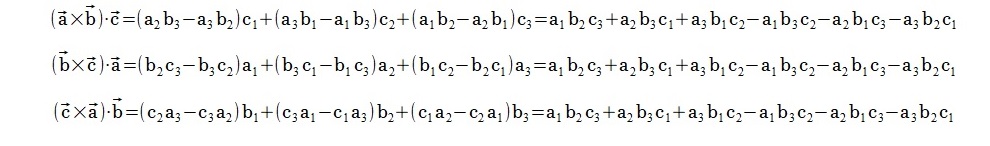
��̊O�ς́A���Ȃ炸�Aa��b��c��a�̏z�ōs���Ba,b,c����,��,���n�Ɠ������̊W�ł���ΐ��ł���B
���ꂪ�R�̗�x�N�g���łł����u�X�J���[3�d�ςł���A�R���R�s���v�ł���B
�X�J���[3�d�ς�[�P�ʃx�N�g��]������ƁA1�����������ĂO������]���q�W�J�Ƃ��Ċy�ł���B
�P�ʃx�N�g���������Az���������邩��A�P�ʃx�N�g���̗�ɂ��]���q�W�J�ŏ�L�̂悤��3�ʂ�\��������B
�@�u�s�x�N�g���Łv����Ă��s�̌��ʂ͓����ł���B
��ڐ��A�s�ڐ��ǂ����ł������̂����A��x�N�g���͈ꎟ�ϊ��Ŋ��K�I�Ɏg���邾���ł���B
3���������@�s�́A��x�N�g���������͍s�x�N�g���̈ȉ��̃X�J���[3�d��
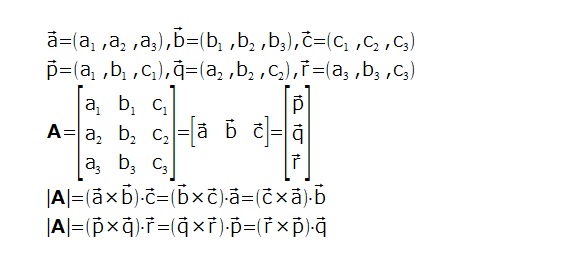
3�������x���Ȃ�A���ϓI�����L�̇@�A�B�̍s��̊ȑf���̂��Ƃ��킩��₷���B
�E�@�s�������ւ��邱�Ƃ́A�X�J���[3�d�ς̊O�ς̏��Ԃ��ς��A�s�͐����̕������ς��B
�@����́A�s�������ւ��čs�����߂�Ƃ��ɂ̓}�C�i�X��t�����B
�E�A�s���œ������̂��Q����ƁA�X�J���[3�d�ς̓����x�N�g�����m�̊O�ρ��O�Ȃ̂ŁA�s���O�B
�@�@���L�̇B�A�s�������͗�̐����O�ɕό`�ł��A�]���q�W�J�ōs���O�ƂȂ��Ă��܂������B
�E�B����s�ɁA�ʍs�̉��{���������i������l�j���Ă��X�J���[3�d�ς������Ȃ�����A�s�����߂�Ƃ��g����B

�������ɂ��āA�ȉ��̂悤�ɁA�u�s�����߂�̂ɓs���̂悢�s��ɕό`�v����Z���g����B

�[������1�s��1��ڂ�3�s��3��ڂƂ��́A�]���q�͑f���ɍs�Ɨ����菜�����Q���Q�s�ł����B����ȊO���ƃ}�C�i�X���t���Ƃ�������ˁB
����́A�s�������ꂩ���Ē[�����Ɏ����Ă��Ƈ@�̂��Ƃ��N����̂ŁA�\�z�ł��邾�낤�B�s�Ɨ�̘a������������Ō��܂�B1�s2��ڂ��ƂP�{�Q���R�Ŋ������A�}�C�i�X���t���B
��{�I�ȍs��̕\����@�A���̂Ȃ��@�@

�⑫�Ƃ��ẮA
���@�]�u�s�������ɓ]�u�s��Ƃ��Ƃ̍s��ɖ߂邾���ł���B
���@���łɏq�ׂ����A�s��̐ς̌��ʂ�]�u����ƁA����͓]�u�����s�u�̊|���Z�ɂȂ邪�A�|���鏇���͋t�ɂȂ�B
���@�Ίp�s��͑Ώ̍s��ɏ�������i�n��E���Ώ̍s�Ίp�s��̈��ł���j�B�Ίp�s�u�̉��Z�͐������Ίp�����Ȃ��v�Z���X�J���[���ۂ��Ċy�ł���B
![]() �u�s��̐ρv�Ƃ́A�u���ς��������߂Ă���v����
�u�s��̐ρv�Ƃ́A�u���ς��������߂Ă���v����
���̂Ƃ��A�s����Ă̂́A�x�N�g������ׂ����̂ƍl��,
3�~3�s��Ȃ�A3�����x�N�g����3�s���ׂ��ƌ��邩�A3����ׂ������B
���������ɕ���ł���̂������x�N�g������Ȃ� �ia,b,c�j�̂悤�ɕ\������������Z�ł悭�������������A����͕X��J���}�ŋ���ĉ�����������1�s�ɏ����₷�����炾�B
�e�v�f���c�ɂȂ�ׂ��\�L�͗�x�N�g���Ƃ����Ĉꎟ�ϊ��ł͂悭�g����B�v�f�����ɕ��ׂ�x�N�g���͍̂s�x�N�g���Ƃ����B
�u�s�x�N�g���v�~�u��x�N�g���v�̓���
�R�~�R�s��̐ς́A�Ⴆ�A���L�̂悤�ɍ���2�s�ڂ̍s��ف@�Ɓ@�E��3��ڂ̗���قœ��ς��Ƃ�ƁA���ʂ�2�s3��ڂ̗v�f�ɂȂ�킯���B���ǁA���̍s��̂R�̍s�x�N�g���ƉE��3�̗�x�N�g���̓��ςœs��9�ʂ�̓��ς����߂Ă��邾���̂��ƂȂȁB
�@�s�̃x�N�g���@�@�@�@�@�@�@�@�@�@��̃x�N�g���@�@�@�@�@�@�@�@ 3�s�x�N�g��x�R��x�N�g���œ��ς��X�ʂ�
| �� |
�@ |
b1ex |
�@ |
= |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| b2ey | ||||||||||
|
a1ex |
a2ey |
a3ez |
�@ |
b3ez |
�@ |
���E�� |
�@ |
���݂��̃x�N�g������(�����̐��j������Ȃ���Γ��ς̉��Z���ł��Ȃ�
���̗ƉE�̍s������v����Ƃ������@
���ӁF�s��̊|���鏇������������x�N�g���̑g�ݍ��킹���ς���Ă��܂�����A�����̖@���͐��藧���Ȃ����낤�B
���̊e�s��́u�s�Ɨ�̔��]�����v�ς̌`�́A�|���鏇���t���ƒ��낪�����@�i�`�̓]�u�s���tA�Ə����A�s�Ɨ�̔��]�������́j
A x B = C �@�Ȃ�� tB��tA��tC
�@�s�̃x�N�g���@�@�@�@�@�@�@�@�@�@��̃x�N�g���@�@�@�@�@�@�@�@ 3�s�x�N�g��x�R��x�N�g���œ��ς��X�ʂ�
|
�@ |
�@ |
�@ |
�� |
�@ |
�@ |
a1ex |
= |
�@ |
�@ |
�@ |
|---|---|---|---|---|---|---|---|---|---|---|
|
b1ex |
b2ey |
b3ez |
�@ |
�@ |
a2ey |
�@ |
�@ |
���E�� |
||
|
�@ |
�@ |
�@ |
�@ |
�@ |
a3ez |
�@ |
�@ |
�@ |
�t�s����A���ς̒m���ŗ\�z�ł���B
�Q�̍s�x�N�g���ƂQ�̗�x�N�g����4�ʂ�̓��ς̂����A�Q�ʂ�͂O�i���Ȃ킿�j�������Ă���Ƃ������ƂɂȂ�B
��������A�s���ȍ��̍s��ɂ���s�x�N�g���𐄑��ł��邾�낤�B�@�@

| b�~�� | �~ | �� | �� | �� |
|---|---|---|---|---|
| ���~�� | ||||
| ���~�� |
�a�̍s��قƂ`�̗���ق̓��ς̑g���������߂��ƁA��͂� BA=|A|E
|
�a�` |
�� |
�� |
�� |
|---|---|---|---|
|
���~�� |
|�`| |
�O |
�O |
|
���~�� |
�O |
|�`| |
�O |
|
���~�� |
�O |
�O |
|�`| |
��̂悤�ɁA�x�N�g���ŏc���ɕ\�������āA���ς̑g�ݍ��킹9�ʂ������킩�邪�A
�Ίp������
���E�i���~���j���i���~���j�E�����i���~���j�E���@��|�`|�@�@�@�X�J���[3�d��,�������A�O�ς̏��Ԃ͏d�v���`�̍s�ɂȂ�
�㎮�́Aa,b,c�̂�������O�x�N�g���łȂ��Ă��A�����ꂩ�Q�̃x�N�g�������s�������ꍇ�A�O�ς��O�ƂȂ�A���ʁ@�s�͂O�ƂȂ邱�Ƃ������Ă���B
�i�Ɨ������R�̎��ƂȂ��Ă��Ȃ��Ƃ������Ƃł��ˁB�j
����ȊO�̐���
�Ⴆ�A���~���Ƃ�����ق́A�O�ς̒�`������ق�����ق��ō��ʂƂ͐�������قɂȂ�킯������A���b����ق��Ɠ��ς��Ƃ��Ă��O�ł���B
�i���~���j�E�����i���~���j�E�����O�@�A���l�ɂ��āA���ʂƂ��ăX�J���[3�d�ψȊO�͂O�ɂȂ�B
���@|A|=0�̂Ƃ��͋t�s��͋��܂�Ȃ��B���̂Ƃ�BA=O�|�|�|�|���������q�ł���B
�`�̋t�s��Ƃ́A�`�̗������x�N�g��a,b,c�@
�ŁA�\���ł���̂ł���B
�ꎟ�ϊ��ɂ����鐳�K���s�n���ǂ����̓x�N�g���̓��ς̒m���ł킩��
�f�J���g���W�̂悤�ɑ傫���P�Ō݂��ɒ���������W�������A�����������ƂȂ�x�N�g���ōs��A���ł��Ă��邱�ƁB
����́A�����̍��W�łł�������}�`��ϊ����Ă����̌`��ς��Ȃ��i���]�������͉�]���邾���j�̕ϊ����Ƃ������Ƃ��B
A�̓]�u�s�t�s��ɂȂ邱�Ƃł���B

�`�a���a�`�͈�ʂɐ������Ȃ��B����s��ƒP�ʍs��ł��Ă���Ƃ��B
�����̖@���͈�ʓI�ɐ��藧���Ȃ��BAB=BA�@�͓���ȏꍇ������������

A�́AB�̃X�J���[�{�ł��P�ʍs��̃X�J���[�{�ł��Ȃ��ꍇ
AB=BA����ʓI�ɐ��藧��B�́AA��E�̈ꎟ�����ł��邱�Ɓ@�����n���Ɋm�F���Ă݂�

���łɁA�n���Ȍv�Z��|AB|=|A||B|���m���߂Ă݂���
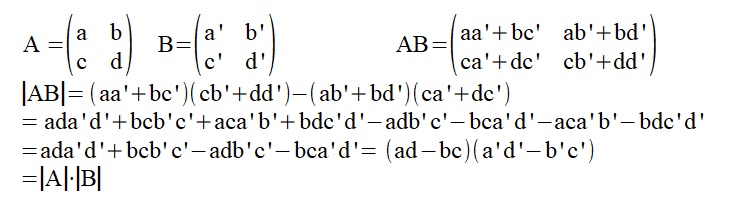
�`���a���n�łȂ��Ƃ��ɂ`�a���n���������邱�Ƃ�����B
�t�s���T���ߒ��ŁA�s��̐ς�O�ƂȂ肤��P�[�X�����邱�Ƃ����łɂ���Ă���B
A�̍s���O�GA�̋t�s��i�ς̋t���j���Ȃ��Ƃ��ɂ́ABA=O�@�ƂȂ�B������B
�X�J���[�ł́A�O�łȂ����ɂ͕K���|���Z�̋t���i�t���j�����݂���.
�s��ł́A�u�s�v���O�łȂ��s��ɂ͊|���Z�̋t���i�t�s��j�����݂���B
�E�O�łȂ���a�́A�i�P�����̐��Ŋ����̂Łj�t��1/a�����݂���@
�E�s���O�łȂ��s��́A�t�s���܂�B�@
�Eaxb���O�Ȃ�A�K���Aa,b�ǂ��炩�͂O�ł���B
�EAB��O�Ȃ��A�K������A,B�ǂ��炩����s��Ƃ͌����Ȃ��B�K���ǂ��炩���s���O�ł���Ƃ������Ƃ͌�����B
�@����A�̍s���O�Ȃ�AA�ɏ�@�̋t���͑��݂��Ȃ��AA�ɑ��ė�s��łȂ�����qB�����݂���B
![]() �Q���Q�s���ɂ��ẮA��قǂ̒ʂ�A����Ɍ����̖@����OK
�Q���Q�s���ɂ��ẮA��قǂ̒ʂ�A����Ɍ����̖@����OK
�@
��L�͍s��`�̌ŗL�������Ƃ��������`�̎��̎�����������Ƃ��Ɏg����
��҂̃X�J���[�ϐ��Œu�����������́A�ŗL�l�������ŁA�s��`�̌ŗL�l�����߂���̂ƂȂ�B
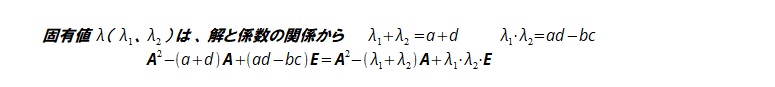



�s��̌ŗL�l���g����2���Ȑ��̕��ނ֔�т܂�
���f���̌ŗL�l�������A���f���̎����E�������s��̐����ɑΉ��ɂ�����̂�����B
����́A���f�����s��\���ł���b�ƕ������Ă���B

���f���̍s��\���A4�����̍s��\���ւ̃����N
�@
�t�s��̘b���A�]���q���g���ĕ\��
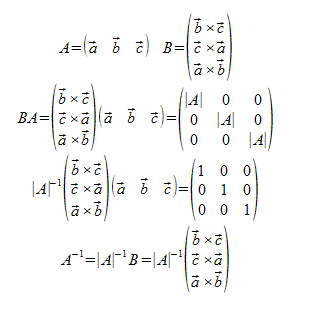
�ȉ��A�]���q�ɒu�������āA�b������B
�s���u����s����̃x�N�g���v��I��ŁA�u���̗]���q�R�����łł����x�N�g���v�Ƃ̓��ςƂ������邱��

���L�̋t�s��̋��ߕ��́A�Ώ̍s��Ȃ̂Ł@�]�u���Ȃ��Ă������]���q�Ȃ̂ŁA�킩��₷���A��ł��ˁB
�s���ǂ����Ƃ����ƁA�Ίp�������O�ŁA�T���X�̒藝�i�߂ɂ������́A�t�߂͂O�j�@�����@2abc�@�Ɓ@�킩��B

�ꎟ�ϊ��@���̃y�[�W
![]() �����Ȃ����̂ŁA�����E�ϕ��̘b�͂܂�����Ƃ��悤�B
�����Ȃ����̂ŁA�����E�ϕ��̘b�͂܂�����Ƃ��悤�B
�@