回転を使ってみて、曲線の式を見てよう

x2、y2、xy、x、y、定数であらわされる　x、y 2次多項式＝０というｸﾞﾗﾌ ax2＋2bxy＋cy2＋2dx＋2ey＋f＝０
（係数2をつけているのは、そのほうが変形上、都合がいいから） ただし、２次曲線だから、x2、y2、xyの係数　a､b､c　すくなくとも、いずれか1つは０でない。
おそらく、適当な平行移動と回転の1次変換で、2次曲線の標準形にできるだろう。

以下の標準形になるだろう、標準形にはxy項が無いので、xy項の無い式にしてみないとわからない

式を満たすｘ，ｙの実数値が存在しない式は除いて、楕円、双曲線、直線、１点、放物線のいずれかに分類できる。

円錐曲線：
ｘ，ｙという２次の式であらわされる２次曲線は、互いに頂点で倒立した２つの円錐に対し、ある切断面をとるとできる曲線である
ただ以下のようなケースは円錐曲線としては、どうしたらいいかわからない


たまたま、うまく変形できると、どんなものかわかるやつもある。

因数分解できれば２直線である。
(ｘ−２ｙ＋１)(４ｘ＋ｙ−７)＝０　　　　　　　ｘ−２ｙ＋１＝０　または　４ｘ＋ｙ−７＝０

２乗和なら2直線の交点である１点である。
（ｘ−２ｙ＋１）２＋（４ｘ＋ｙ−７）２＝０　　　ｘ−２ｙ＋１＝０　　かつ　　４ｘ＋ｙ−７＝０

因数分解したら因数が同じ、すなわち２つの直線でなくて１つに一致してしまう。
（ｘ−２ｙ＋１）２＝０　　　
これは、円錐曲線という点で考えると、２直線だと、倒立した円錐同士の接点である円錐の頂点を通るような切り口なわけだが、
平面を傾けていって母線そのものになったら、１つの直線である。さらに傾けると１点になる。

９（４ｘ＋３ｙ）２＋４（−３ｘ＋４ｙ）２＝３６　　たまたま、cosθ＝４／５、sinθ＝−３／５　の回転がなされた座標に置換された楕円の式である。

こういう、たまたま因数分解や完全平方の変形などで、できるケースでなければ、適当な平行移動と回転をして以下のどの標準形になるかをやって曲線がどうなのかってのをやるんだね。
上のような標準形のｘ、ｙの替わりに一次式が置換された形に、力ずくでもっていければいいけども。

（Ｘ、Ｙ）がＸＹ＝ａという反比例ｸﾞﾗﾌ上の点としよう（Ｘ，Ｙ）という点は、ある（ｘ、ｙ）を 45度回転した点と仮定すると
cosθもsinθもθ＝45度のときは、√2／２＝２-1/2だから　回転の一次変換の式から
Ｘ＝２-1/2（ｘ−ｙ）　　　Ｙ＝２-1/2（ｘ＋ｙ）
ＸＹ＝ａ　を満たすという条件だから上の式を代入して、ｘ，ｙで整理すると　ｘ2−ｙ2＝２ａ

このようなx座標とy座標の関係は、直角双曲線を表す標準形の式そのものなんだな。

楕円の特別なものが円であるように ｘとｙの二乗の係数が一致するとき双曲線の場合は、直角双曲線なんだな。

ａが負のときは両辺に−１をかけて左辺 ｙ2−ｘ2 とすれば、右辺が正になるので、ｙ軸に交わる方の双曲線の式の形である。
これは、反比例でａが正か負でｸﾞﾗﾌの出てくる象限がどこなのかに対応している。反比例のｸﾞﾗﾌは直角双曲線の標準形を４５度回転したものであり、曲線の種類としては直角双曲線であったことが明白になる。
次に（Ｘ、Ｙ）がＸ2+Ｙ2＝ａ2という円ｸﾞﾗﾌ上の点としよう　これは、原点で回転しても　円上にあるので、円のグラフはそのままでかわらないと予想される。
（Ａ）、（Ｂ）の式から
Ｘ2+Ｙ2＝(cosθ･ｘ−sinθ･y)2＋(sinθ･ｘ＋cosθ･y）2＝(cosθ2＋sinθ2）ｘ2＋(cosθ2＋sinθ2）y2＝ｘ2＋y2
楕円であればxyの項が消えないので、こうはならない。

また、別のｸﾞﾗﾌでも双曲線らしきものに高校数学で遭遇しているはずである。
※　下記は　ｘ←x-1、y←y-1　と記載してあるけども　ｘ→x+1、y→y+1という置換といっしょのことです。

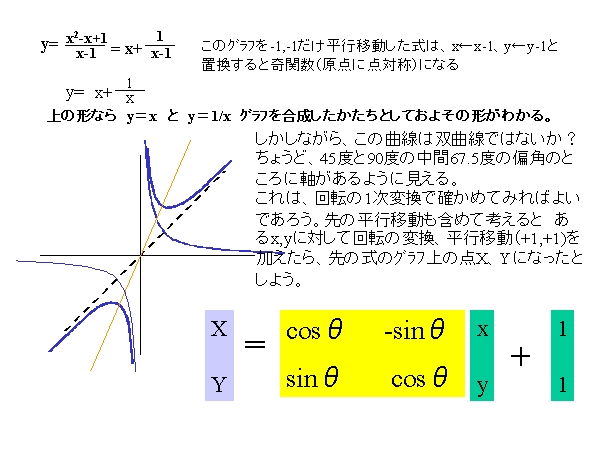
分数式となった整式の関数式である。下のような式のｸﾞﾗﾌは、双曲線の回転と平行移動であろう。

上の行列の計算式　Ｘ＝，Ｙ＝　を もとの「Ｙ＝（Ｘ2-Ｘ＋１）／（Ｘ−１）」を満たす点として代入してみると

(sinθ−cosθ)x2cosθ−(sinθ+cosθ)y2sinθ＋(cos2θ−sin2θ＋２cosθ・sinθ)xy　＝　１

加法定理で整理すると
（sin2θ−cos2θ−１)/2・x2＋（cos2θ−sin2θ−１)/2・y2＋(cos2θ＋sin2θ)xy　＝１

上式でｘｙの項　cos2θ＋sin2θ=0　にするような回転角度θがあれば、上記は下記に示す双曲線の標準形（ｘｙ軸対称）になる。

±｛(αｘ)2−(βｙ)2｝＝１　双曲線の標準形：x,y軸と原点に対称な形っていうのが標準なのでね。
まあ、２次曲線（楕円、双曲線、放物線など）で、xy項というのは標準形（x軸かy軸に対称な形）にすると実は現れてこないんですね（ある条件で派生して出てくるものであって）。

このxy項の係数は、…・・「三角関数なのでいろんな求めかたはあるが」

2つの式は、x二乗とy二乗が異符号だから双曲線である。しかも係数からして、長軸が違うだけで形は同じである。
やはり与えられた式は、予想通り　「ｙ＝ｘ」と「ｙ軸：ｘ＝０」という斜めに交わる2直線の中間に対称軸をもった双曲線だったのである。この２つの直線が双曲線の漸近線なのだ。

双曲線の例を２つ出したが、式を整理すると xy-a＝０　と　x2-xy-x＋y+1＝０ となる

2次式を見れば簡単にどんな種類のものか、わりとすぐわかるケースもあるね。xy=a を基本に考えるとx=0とy=0が漸近線である。直交するから直角双曲線だ
ｘ2−ｙ2＝２ａという形は、(x-y)(x+y)=2a　漸近線がx=yとy=-xになったと考えられる。これも2直線が直交する。
x2-xy-x+y+1＝０　についても、(ｙ−ｘ)(ｘ−１)＝１漸近線がy=xとx=1になったと考えられる　こいつは45度で交わる漸近線だ。

高校生の知識でも、このように力ずくでやれないこともない。
ただし、２ｘ２行列が高校の課程であったときの話ですけど、最近は行列なくなったとかあるらしいけど？

ax2＋2bxy＋cy2＋2dx＋2ey＋f＝0

標準形で、
どうしても邪魔なのは「ｘｙ項」であるから、その係数を０にするような回転の角度θを見つければ良い。　
※　行列をつかったり、完全平方つかったりの都合上　2b、2d、2e　なんて　わざと係数２をつけていますが、本質的な意味はありません。
「xy」項、有り・無し　で話は大きくかわる。
係数ｂ=0、すなわちｘｙ項がなければ　ａx２＋ｃy２＋2ｄx＋2ｅy＋ｆ＝０　　
ac≠0なら　　ａ(x+d/a)２＋ｃ(y+e/c)２＝定数　　　と　変形できるから、標準形を平行移動しただけである。
あとは、a,c,定数の符号の正負でもって、放物線以外の２次曲線の標準形の分類になるだけである。
ac=0　なら　　（ただし、aとcが同時に０だと2次式にならないから、それは無しよ）。
ａ(x+d/a)２＋2ey＋定数=0　　放物線の平行移動形に変形できる。
ｃ(y+e/c)２＋2dx＋定数=0　　放物線の平行移動形に変形できる。

「ｘｙ」項が無い b=0　 回転する必要がない　　
「ｘｙ」項がある b≠0　回転する必要がある

これも、同様な力技でなんとか求まります。

実は　a=cのときについては
　実際のｘｙ項を０にする条件では、　ｘ、ｙを入れ替えても成り立つ対称式(y=xに対称）を平行移動したものと予想され、角度が±45度は満たすことがわかる。
ax2＋2bxy＋ay2＋2dx＋2ey＋f＝a(x2＋y2)＋2bxy＋2dx＋2ey＋f=0
およその予想がつくのだが、
平行移動でx,yの一次項を消すと、ｘとｙを交換しても成り立つ「対称式」　y=xという直線に対称なので±45度回転だとわかる
x＝２-1/2（X−Y）　y＝２-1/2（X＋Y）なので　　xy＝1/2（X2−Y2）、 x2＋y2=X2＋Y2 　　　変換されてｘｙの項はなくなる。

(a+b)X2＋(a-b)Y2＋21/2{(d+e)X＋(d-e)Y}＋f=0　　標準形の平行移動した形である

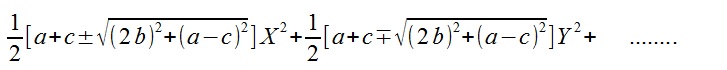
双曲線のときと同様なやり方で,力ずくでやってみましょうか。

とはいえ、大学への数学向けに近づくには、もうちょっと式の変形には2次の行列を使った別のやり方を示すことにします。
それは　こちらです。==>回転してみる　別バージョン　発展形へ

上記の結果だが、一次の項もじゃまだから先に消しておきたい。だから事前に平行移動しておくことも考えよう。

平行移動を先にやることは有効なのだろうか
まず、ｘ、ｙ　一次の項をなくすには平行移動を試すが、もし、　ax2＋2bxy＋cy2＋定数＝０　という形になるのであれば、
(x,y)の代わりに（-x,-y)をいれても成立する式になるから、原点における点対称な曲線であるはずである。
楕円や双曲線は原点対称になるから有効な手段だが、「放物線には無効だろう」
（放物線は曲線が点対称ではない、おまけに軸が回転したままなら平行移動しても座標軸の対称性すら無い、なのでさっさと回転させたほうがよい）　


α、βだけ平行移動したとして、　x→x-α,ｙ→y-β　　と置換してみることだ。
　一次のｘ項、ｙ項が０になるような　α、βが求まればいい　
a(x-α)2＋2b(x-α)(y-β)＋c(y-β)2＋2d(x-α)＋2e(y-β)＋f＝0
ax2＋2bxy＋cy2＋2(d-aα-bβ)x＋ 2(e-bα-cβ)y＋aα2＋2bαβ＋cβ2-2dα-2eβ＋f＝0
ax2＋2bxy＋cy2＋2(d-aα-bβ)x＋ 2(e-bα-cβ)y＋α(aα＋bβ)＋β(bα+cβ)-2dα-2eβ＋f＝0
ｘとｙの一次の項が０になる条件は、以下の(1)となる。
d=aα＋bβ、e=bα+cβ　........(1)
ax2＋2bxy＋cy2 +dα+eβ -2 (dα+eβ)＋f＝0
ax2＋2bxy＋cy2 - (dα+eβ)＋f＝0

上の例だと、Aが逆行列を持たない　行列式　ac-b2=0 のときは、αとβが見つからないから困るが、放物線型である。
特殊なケースは平行な2直線などである。
楕円型とか双曲線型とか有心な形は　平行移動できる（ac-b2≠0）　ax2＋2bxy＋cy2＋定数＝０　という形になり、2次の項だけが残るが、こうしておくと、先の回転させてみるだけで一次の項は無視で済むので有効であろう。

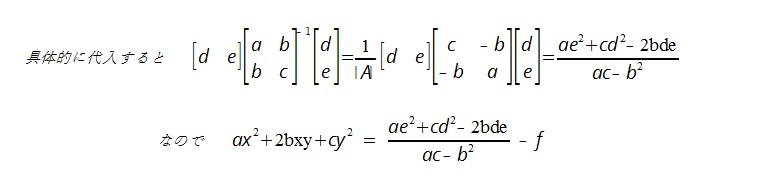
ある特殊な条件以外では、ax2＋2bxy＋cy2の形が2次曲線を特徴付けるもので、一次の項は余談だということがわかるだろう。
大概は 「平行移動でx,yの一次の項を消す＝＞回転によるxy項を消す」　この操作が一番使えそうだと。

２次の係数同士が同じ符号なら楕円型、異符号なら双曲線型である。

2次の係数の判別式って　 ac-b2 =Aの行列式と一緒じゃん
おや？　Aの行列式の正、負、０で楕円型、双曲線型、放物線型が対応してくる話になる。
==>回転してみる　別バージョン　発展形へ

ac-b2=0 のときは、無中心の曲線で先に回転させれば、ｘｙ項と同時にｘ二乗かｙ二乗のどちか一方が消える放物線型のようである
回転させれば　　Y=係数ｘ2　でも　X=係数ｙ2　　どちらも形状は一緒なので、一方だけにする

例えば、2次式の元のx,yの代わりに-x,ｙを代入すると、その曲線はy軸対称で反転する。しかし曲線そのものは形状としてはかわらない。
そのとき、bとdの係数は符号が前の式とは逆になる。bが+5でdが-8だとしたら、bが-5でdが+8でも形状はかわらないはず。
dを含んだ結果の上記の放物線の係数の値は、かわらないはずであるから、bが正のときd＝-8で成立した式に、dの値として変わりに+8をいれたら値は変わってしまう。bが負のとき、結果の式がbが正のときとはdの符号が変わっているのは辻褄があう。

整理された式ではxy項の有無の場合分けではない
すなわち、　b=0か否かでなくて、ac-b2＝0か否か　というふうになる

　
楕円型や双曲線の標準形はx軸、ｙ軸の両方に同時に対称性があって、X2乗とY2乗の係数は逆のパターンがある。
放物線の標準形は、　Y〜X二乗系の正負係数、　X〜Y二乗系の正負係数　放物線の頂点の向きが4通りあるが、どれも形が同じで、とりあえず１つだけ示し、符号のパターンはやめにした。
（目的が曲線の分類であるから）

==>回転してみる　別バージョン　発展形へ