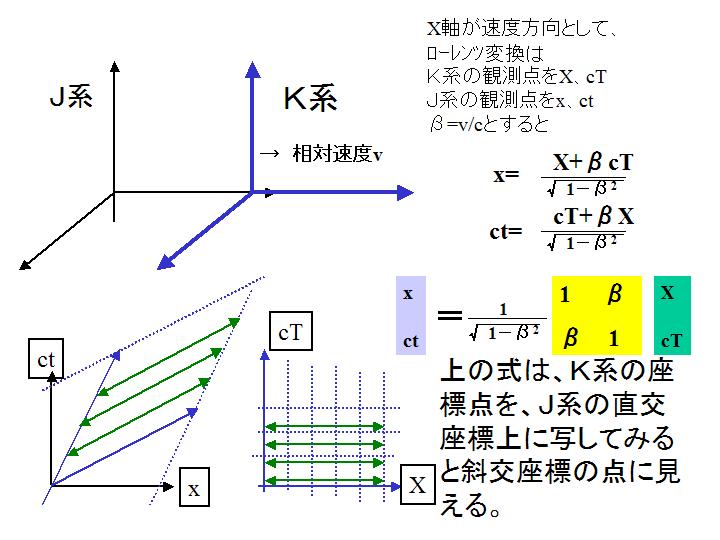
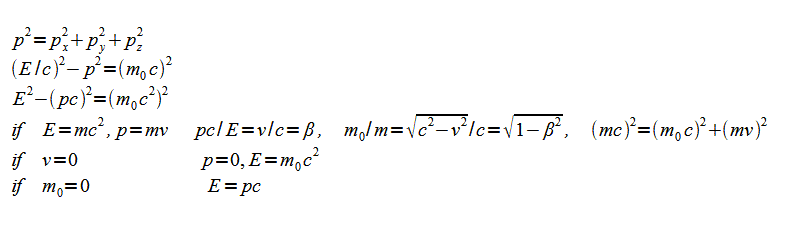���̂Q��4�������W�@(x,y,z,ct)��(px,py,pz�CE/C)�ɂ��āA�s�m�萫���_�ɂ����ẮA�o����4�����v�f�ɂ܂������Đ����̊֘A�������Ă���B
x,y,z���W�Ɖ^���ʂ�x�Apy�Apz�̑g�����A���ԂƃG�l���M�[�̑g�������s�m�萫�̑g�����ł���B
�Ⴆ�@��x�E��px�@�͂�����ȏ�̒l�ƂȂ�A�s�m�萫������
(1)���ʂ̂�����̂̏ꍇ
���������Ƃ���Ƃ��͐Î~���ʂł͂Ȃ��B�܂��AE�^���������ł���B
�����̑傫�����A�O�����̒藝�̎��ɂȂ���̂����邪�A
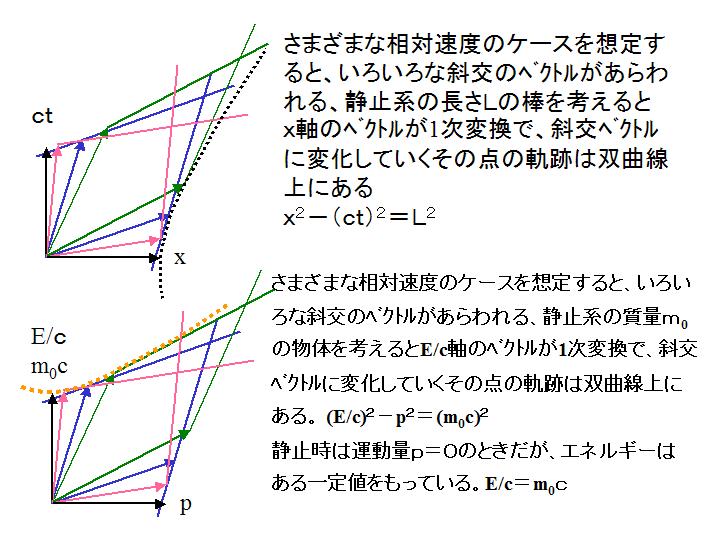
������o�Ȑ��̎��ňڍ������`�Ł@ (��c)2��(��0��)2�{(����)2
�������u���z�I�ȑS�^���ʂ����v���A�^���ʂ����Ƃ���ɒ������鐬���̉^������0���́@�a(�x�N�g���a�j�ōl������H
�u���ʂ��̕����̉^���ʁv�Ƃ���ɒ�������u�Î~���ʁ~�����v�̉��z�I�ȉ^���ʂ���������Ɓu���ʂ��~�����v�̉^�x�ʂ̂悤�Ɍ�����B
P=(px,py,pz,m0c)�Ƃ���4�����^���ʂ�����Ƃ���ƁAmc�Ƃ����傫���ŁD�D�D�@E=Pc�ƂȂ�B
����́A�G�l���M�[�̒l�̑傫�������̂悤�ȉ��z�̉^���ʂŌ��܂�Ƃ������Ƃł���B�萔�̂����������Ă��邩�ǂ��������ł���B
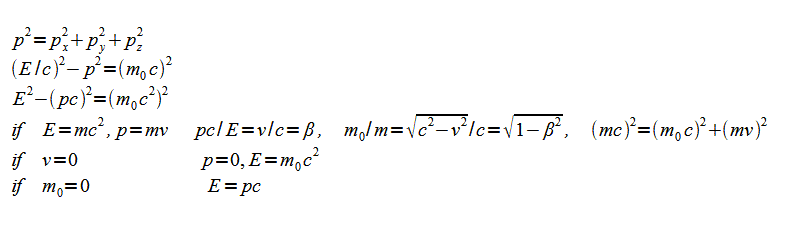
(2)�Î~���Ă��镨���@�����O�ʼn^���ʂ͂����������O
���3�����Ɍ����Ȃ������ɏ�Ɉ���m0c�Ƃ����^���ʁi��ɕۑ�����Ă���j�������Ă���Ƃ������ƂɂȂ�B
�^���ʂ����Ƃ��̒��𐬕�mv��������Ă����������Ă��������ł���B
�G�l���M�[��4�����I�Ɋς��^���ʂ̑傫���ł��낤���B���ʂ��Ƒ��x���ł���Ƃ����悤�ȉ^���ʂł���B
�����萔�Ȃ̂ŁA���ǑS�G�l���M�[�͂��̂��Ƃł���B���͈��Ȃ̂ŕω�����̂͂��ł���B
3�����Ō����Ă���̂��ʏ�̉^���ʂ����Ƃ������Ƃł��낤���B�������Ȃ���ǂ�ȕ�����3�����Ō����Ă��Ȃ��������܂߂Ă݂ȍő呬�x��������Ƃ������Ƃ��B4�������x����3�����Ɏˉe���ꂽ���������ł���A�����̎ˉe���^���ʂ����ł��낤���B
(3)���q�̂Ƃ��͋t�ɐÎ~���ʂ��O�ŁA
�d������
�o�Ȑ����Q�ߐ��̂Q�����@(E-pc)(E+pc)=0�@�ɂȂ����ƍl���Ă��悢�B
�Î~�G�l���M�[�͂Ȃ��^���ʂ̑傫�����G�l���M�[���̂��̌��߂�B
���q�́A�ϑ��҂Ɠ����n�ŋt�ɐÎ~���Ă��邱�Ƃ��ł����A���x����Ɏ����z������ď����邩�����Ȃ��B
�^���ʁi�x�N�g���Ȃ̂ʼn^���ʂ̑傫���F��Βl�Ƃ����ׂ����j�ɒ萔c�����������̂��G�l���M�[�Ƃ����������A
�i�P�j�i�Q�j�����z�I�ȑS�^���ʂ���,��0���������Ƃ���ƁA
����ɒ萔�����������̂��G�l���M�[�Ƃ��������悤�Ȑ����̂������ɂ��Ȃ肤��B
�������Ȃ���A
�^���ʂ̓x�N�g���ʂł��邪,�Ƃ肠�����́A�G�l���M�[�͂����܂ŃX�J���[�ƍl���Ȃ��Ƃ����Ȃ����낤�B
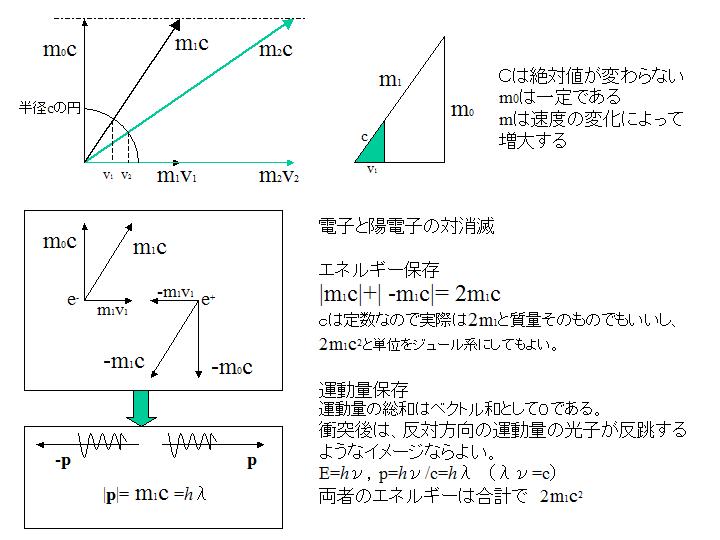
�d�q�Ɨz�d�q�ɂ��Ώ��łȂǂ͎��ʂ��Ȃ��Ȃ�̂�
���z�����̉^����m0c�̐������ł����������悤�ȉ��z�I�ȃx�N�g������������Ƃ����ӂ��ɍl����ׂ��Ȃ̂�������Ȃ��B
���ꂼ�ꂪ�����Ă����G�l���M�[�̓x�N�g���̑傫���Ƃ��ăG�l���M�[�ۑ��i��Ηʂ͂����Ȃ��j����A�Î~���ʕ����̃x�N�g�������������邪
�G�l���M�[�̐�Ηʂ�2���q���̌��q�̃G�l���M�[�ɕς��B
���̂Ƃ��Î~���ʁ~�����Ƃ������������͂Ȃ��Ȃ��āA���̉^���ʂ݂̂ł���B
���������ΕӂƂ��Ă�����ӂ����Ƃ������p�O�p�`�ƁA���������ΕӂƂ��Ă�����ӂ�Î~������0�Ƃ������p�O�p�`�������`�ɂȂ邪�A�ӂ̑Ή��W�͂�����0�ł͂Ȃ��B
�܂��A�����̏ꍇ�͂����Œ�ł��邪�A���ʂ̏ꍇ����0���Œ�ł���B
��ԕ����Ƃ͒������Ă������z�I�ȉ^����m0c�̐������ł����������悤�Ȕ��̐����Ƃ́A���낢��Ȏ���������悤�ł���B
�t�@�C�}���̋c�_�������߂Ă����ƃQ�[�W���_�ɂȂ�B
��Ԃ�x���A���Ԃ�y���̃C���[�W�œd�q�̋O�Ղ�����Ƃ���͓d�q�̐��E���Ƃ���
��ԂɐÎ~���Ă����ԍ��W�����Ԍo�߂ł����Ȃ��̂Ő����Ȑ��ł���B
�X�����������̂́A���Ԃ̌o�߂ɑ��ċ�ԕ����ւ̈ړ��������̂ő��x�̑����E�^���ʂ�G�l���M�[���傫���d�q�ł���B
���̊G�̃C���[�W�͐��E�����Ȃ���Ƃ���Ō��q�̕��o�E�z���Ő�����������ł���B
�E���x��������悤�ȏꍇ�́A����̒��ɕ��荞��}�������������d���g����o���邱�Ƃ�����B
�E�����z�����đ��x�𑝂��ꍇ�Ȃǂ�����B
�E��U�A������o���Ăقڒ�~��ԂɂȂ�A�����Ɍ���ʂ̂Ƃ��납��z�����Ĕ��Ε����֓��������B
�E�Q�̓d�q���߂Â��Č݂��Ɍ�����o���A�݂��̌�������ċt�����֓����o���B
�@���Ȃ킿�A����͏Փ˂��Ē��˕Ԃ�C���[�W�ł���B�d�����ݍ�p�����q�̌����Ő�������鏊�Ȃł���B
���ӁF���̐����ł͐����̓d�ׂɓ������͂̐����ɂ͂Ȃ�Ȃ��B
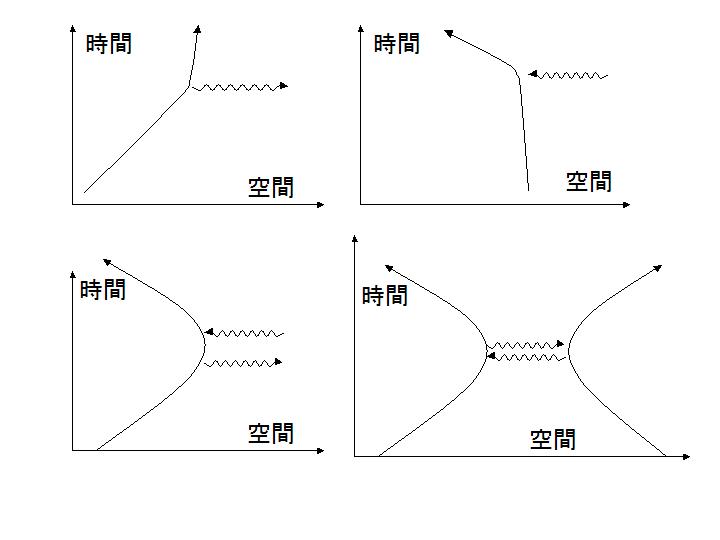
���E�����ߋ�����������ȓd�q������Ƃ���ƁA�����̋Ȃ������Ƃ���ł����q�̕��o���z��������B
����͎��Ԃ̌o�߂ƂƂ��Ɍ����
���鎞�_�œd�q�Ɨz�d�q������A�ʂ̎����ɂ͓d�q�Ɨz�d�q�̑Ώ��ł��N���Ă���Ƃ����}���ɂȂ�B���Ԃɋt�s�����d�q�̐��E�����z�d�q�Ȃ̂ł��낤���H
�d�q�̐��E�������܂ɂ��̂悤�ɘc�ނ̂ł���A�z�d�q�͕��i�߂����ɂ��ڂɂ�����Ȃ����A�Ώ��ł��Ď������Z�����낤�B
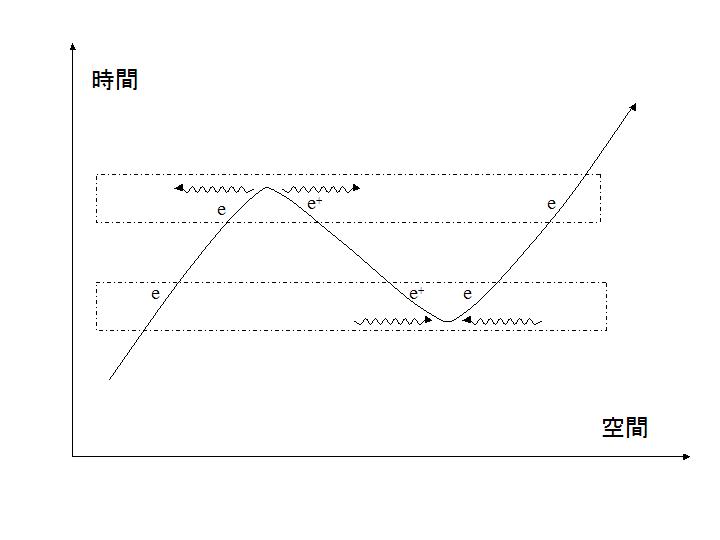
�ЂƂ̓d�q�̐��E���Ƃ��Č���A
�ŏ��̋Ȃ���p�ŁA���̓d�q�̑S�G�l���M�[�ȏ�i2�{�ȏ�́j�G�l���M�[����o���邩��A�d�q�̃G�l���M�[�͕��ł���B
���̋Ȃ���p�ł́A�t�ɓ�{�ȏ�̃G�l���M�[���z�����Ă���B
���Ԃɋt�s�������E���̕��������̓d�q�̃G�l���M�[�Ƃ������ƂɂȂ�B
���̎��Ԃɋt�s���Ă���Ƃ������ƂƃG�l���M�[�̕��ł���Ƃ������Ƃ̊W�Ƃ͂ǂ����������̂��B
�����ėz�d�q�͓d�ׂƂ��Ă��z�Ȃ̂ŋt�ł���A�������Ƃ͉��Ȃ̂��B
������A�s�m�萫���_�ł̓G�l���M�[�Ǝ��ԂƂ̕s�m�萫���ɂȂ�B�������ƕ����̑Ώې��́A�ʏ�͈��|�I�ɔ�����������Ȃ��B
����͎��Ԃɑ��Ă������ł��낤���A����f���q�̔����̂Ƃ������������Ԃ̋t�s�Ƃ͌���Ȃ��Ƃ����㕨�Ȃ̂ł��낤���B
�t�@�C�}���̌���
�u���Ԃɋt�s�������E���̓d�q���z�d�q�ł���v���ꂾ�ƁA�z�d�q�͕��̃G�l���M�[�̓d�q�̂悤�ł���B
�f�B���b�N�̌���
�u���̎��ʃG�l���M�[�����d�q���^�ɏ[�����Ă��āA�^���N���ēd�q���ł���Ȃ�A�d�q��2���̎��ʃG�l���M�[�̋z�����K�v�ł���A���Ƃ̕��̃G�l���M�[�d�q�̂������ꏊ�����E�ƂȂ�z�d�q�̂悤�ɂȂ�v
�Ƃ����c�_�ł���B
�t�����Ƃ͎��ԕ������t�Ȃ̂��H���ʁi�G�l���M�[�j���������t�ɂȂ��Ă���̂ł��낤���HCPT�Ώ̘̂b��ǂ炨�����낢���낤�B
�O�̃y�[�W
http://www.ne.jp/asahi/imaimai/homepage/ index�ɖ߂�
�@