�u��]�̍s��v���g�����ז��Ȃ�����������(�ʃo�[�W�����j
�ȉ��̋c�_�ŁA
b=0�̂Ƃ�.........���������Ȃ����s�ړ��ŕW���`�ɂȂ�̂��o���Ă���B
a=c�̂Ƃ�.........�Ώ̎��i�Ώ̎����}45�x�̉�]�j�̕��s�ړ����ꂽ���ƍl������B
��L�̂悤�ȓ���ȏꍇ�́A��J�͂��Ȃ��B
�����Aac-b2=0 �łȂ���A�_�Ώ̂̋Ȑ��Ȃ̂ŁA���s�ړ����ɂ���B
�����ł́A�O�ɏo�Ă���
�ȉ��̗�x�N�g���ƍs�x�N�g���ŁA�\���̎d���������������� ���Ă̂��g���B�@�ꎟ�ϊ�
��̕��s�ړ��̇B�̌`�Ƃ��ł��g�����ό`���@��]��2���Ȑ����@
��]���ꂽ���W�n��XY�����Ȃ��Ȃ邱�Ƃ�ڎw�������킯�ł��邩��

�������́A�O�p���̍����ɕό`���ď����w�肵�Ă��悢
������ɂ���XY�����O�ƂȂ�����i���̂悤�ȍ��W��]�p�x�̂Ƃ��j�ł�
�@a��c�@�A�@��=2�Ƃ̂Ƃ��@�@tan 2��=2b/(a-c)�@�ƂȂ�B�������ʂł���B
�O�p���̏z������A2��=���}�Ƃ��������̂�����@�@��=��/2�@,�@��/2�}��/2
2���Ȑ���x���ɑΏ̂ł���Y���ɂ��Ώ̐����Ƃ����`������A�������}90�x�̉�]������Ƃ������Ƃł���B
�ŏI�I�ɏ��X,Y�̎��́A���s�ړ��ŕW���`�ɂȂ�B���Ȃ킿�A�K���ȉ�]������ΕW���`�ɂł��邱�Ƃ��킩��B
���̍��W�ϊ��A�ʓ|��XY�����O�ɂ���̂́A�u�s��̌ŗL�l�A����ɂ��s��̑Ίp���v������Ă���B
�O�ɏo�Ă����ŗL�l���������o�Ă���B�����ČŗL�l�̎��𐬗�������ŗL�x�N�g���A
���̃x�N�g���ł���s��͉�]�̍s��ɂȂ��Ă����Ƃ������Ƃ�
�Ȃ��A�s��A���Ώ̍s��ł���Ƃ������ꐫ������̂ŁA��ʓI�ȌŗL�l���Ƃ͎�Ⴄ���Ƃɂ����ӁB
�ŗL�x�N�g���́u�ꎟ�ϊ����Ă��ς��Ȃ� --- ���ʂȕ���������v�Ƃ����u�����̂��Ɓv�ł���A�傫���͔C�ӂɑI�ׂ�B
�����āAA-��E�̍s���Ȃ��O�łȂ��Ƃ����Ȃ��̂��H
�����Ȃ��Ƃ��A�ꎟ�ϊ�A-��E�Ō��_0�ȊO�̓_��0�ɂȂ��Ă��܂��Ƃ������Ƃ͎������k�ނ���̂�����A���̍s��0�ł��邱�Ƃ��K�{�ł���B�s��̐ς̒�`���炵�āA�Q�̍s�x�N�g���Ƃ��ɌŗL�x�N�g���Ɠ��ρ��O�A�������Ă��邱�Ƃł���B
����́A�Q�̍s�x�N�g���ia-��,b�j�Ɓib�Cc-�Ɂj�����s�i�������͔��Ε����j�X�J���[�{�Ƃ������Ƃ��Ba-�ɁFb��b�Fc-�� , �ia-�Ɂj���ic-�Ɂj��b2�@�����|A-��E|���O�̈Ӗ��ł���
2�����̈���ŗL�x�N�g�������������A�������k�ނ��Ē�����Ɉڂ邪�A�ǂ����Ă����_�Ɉڂ�Ƃ������Ƃ��낤�B
�ŗL�l�������̉��������Ȃ�(A-��1E)(A-��2E)=O
��L�̈����������ꂽ�������藧��,�ŗL�l�̒�`���炷��ƈ���̍s��(A-��1E)����݂��(A-��2E)�͑Ή�����ŗL�x�N�g������x�N�g���Ƃ��ĕ���ł���s��ƌ�����B����͋t�̌ŗL�l����������A���͌ŗL�x�N�g�����Ȃ�ł��邩���������������̂��B
���ۂ́A�ɂ͌ŗL�l2���������ŏd���łȂ�������́A2�ʂ肠�邩��A�����̌ŗL�x�N�g������������B�������������łȂ��Ɛ}�`�I�ȃC���[�W�͈Ⴄ�B���Ƃ��Ή�]�̍s��Ȃ�A�S�̂���]���Ă��܂��̂ŁA�����������Ȃ��x�N�g�������ȂǑ��݂���Ƃ͎v���Ȃ��B���ۂɂ́A���͉�]��\�����f��cos�Ɓ{i�Esin�ƂɂȂ�̂��B���f����\������s��̌ŗL�l�͋��f�����ŗL�l�ƂȂ�B
�Ⴄ�ŗL�x�N�g������ɕ���ł���̂�P�ł���Ƃ����ꍇ�͂ǂ��Ȃ邩���Ă݂�B
�o�i�Q�̈قȂ�ŗL�x�N�g���łł����s��j�����s�n�ł��邱�Ƃ́A�u�Ίp�s��ɂ�����ς̌����@���̐����v����ł��킩��B
�Ȃ��A�Ȑ��̕��ނ��u�`���Ώ̍s��v�ł���Ƃ��������́A�]�u�s��ł��ς��Ȃ��ȂǏd�v�Ȑ���������B

�Q�̌ŗL�l����v���Ă��܂��P�[�X�͍l���Ȃ��Ă��悢�B����͂p���P�ʍs��̃X�J���[�{�ɂȂ�A�`�o���o�p���Ƃ`���P�ʍs��̃X�J���[�{�Ƃ����\�z�������A���ۂɌŗL�������́@���ʎ����ia-c)2+(2b)2=�O��������炩��a=c,��=0�ł���A�s��`���Ίp������Ă���,����2���Ȑ��̕W���`��\���Ă��邩��ł���B
2���Ȑ��̌`��₤�̂ŁA �ŗL��x�N�g���Q�́A�ꎟ�ϊ��ō��W���̒�����ς��Ȃ����̂��B
�O�̕ʃy�[�W�L�ڂ����̂܂܈��p�A�܂����������낦���u�Q�̒�������v�ŗL�x�N�g���łł����s��͂ǂ�Ȍ`�Ȃ̂�


�傫���P�̌ŗL�x�N�g����I�ԁA�����Č݂��ɒ������Ă���D�D�D��]�s��̌`�ł����킯�ł���B
�s��A�̌ŗL�l�����߂��
�@��1 X2 �{ ��2 Y2�{�P�����{�萔��0�@
�������̂Ȃ��`�ɂȂ��B����Ȃӂ��Ɍ���ƁA���̗͂������A��w�ŏK�����`�㐔�̘b�Ɗ֘A����Ǝ������₷���̂ł͂Ȃ����낤���H
���ʎ��i���\�ł͂���܂��j�@�Ⴆ�@��1��2=ac-b2���O�@�Ȃ�A���Ƃ���2���̌W�����ٕ����ł��邩��o�Ȑ��ł��낤�Ƃ����\�z���ł���B
�悭�悭����ƁA
�@��1��2�@��A�̍s���@ac-b2��|A|�@��
�Q�̉���1��2���ٕ��������������A������O���̂����ꂩ�ɂ���ā@��{�̌^���킩��B
|A|>0�@�@�Ȃ�ȉ~�^�@�@�@�@�L�S�^�Ȑ��ŁA��ɕ��s�ړ����Ă����]������肪����
|A|<0�@�@�Ȃ�o�Ȑ��^�@�@�L�S�^�Ȑ��ŁA��ɕ��s�ړ����Ă����]������肪����
|A|=0�@�@�Ȃ�������^�@�@ ��1�ƃ�2�̂����ꂩ0�A�@��1 X2 �{��X�{��Y���萔�A ��2
Y2�{��X�{��Y���萔�@�@���̂Ƃ����s�ړ��͐�ɂł��܂���B
�������A
�W����萔�̓���ȃP�[�X������̂ŁA�u2�����v�A�u���̑ȉ~�v�A�u1�_�v�@�ɂȂ��Ă��܂��ꍇ������A�����ӂ��B
|A|=0�̂Ƃ��i�������^�j�́A���s�ړ��̕ό`�@���A���̈ꎟ�̍�����������͂ł��Ȃ����A��0�ł���A��ɕ��s�ړ����Ă����]�ł������B
�������Aa=c�̂Ƃ��́A�Ƃ́}45�x�ł���B
�x�N�g����s��̕\���́A�ȉ��̂悤�ɂȂ��B
�i�������AA�̍s��0�̂Ƃ��́i�������^�j�Ȃ̂ŕ��s�ړ��͂��Ȃ��B
�]�k�ł����A��q|�����͓��ςŃu���P�b�g�Ƃ����B��q|�@���@�u���i�x�N�g���j�@�@|p�����@�P�b�g�i�x�N�g���j�Ƃ����B
�ʎq�͊w�͕��f���܂Ŋg�����Ďg���A�x�N�g���͓]�u����Ƃ��͓����ɋ��f���ɂ���Ƃ�����ʉ��ɂȂ�B
�i�����A�����x�N�g�����m�̓��ς͑傫����2��ƂȂ邱�Ƃ͎����x�N�g���Ɠ����ŁA�������������܂��܂O�Ŏ����������Ȃ��P�[�X�͋��f�����u����v�A����ȃP�[�X�Ƃ݂Ȃ��킯�ł���j
�@
�������^�̓���P�[�X�Ƃ��A2���̍��ł́A�����������ł�����Ă��ƂŁ@
ac-b2=0�Ȃ�A���� ax2+2bxy+cy2=0��x��2���������Ƃ݂��Ƃ��̔��ʎ�=y2(b2-ac)=0������,���S�����`�ɂ����Ă��������B����ƁA���f���̍s��\���Ɖ�]�̍s��̓X�J���[�{�̈Ⴂ�B���̒m������s���Ƃ���ꍇ�����邾�낤�B

�W�����Q�łȂ�����
���Ƃ��Ɓ@�������Ax���A�����́@2b,2d,2e�Ƃ��Ă��邩��A���ۂ̌W���̔����Ă͂߂�

2���Ȑ��̔��ʂ� �܂��2���������̔��ʎ��݂��������B
b'2-4ac>0�@�@�o�Ȑ��@�������@�u2�����v�@(����)2�|(����)2���O�@�̓���P�[�X�͏�����
b'2-4ac<0�@�@�ȉ~�@�@ �������@�u���̑ȉ~�v�@(����)2�{(����)2���|�P�A�u1�_�v(����)2�{(����)2���O�@�Ȃǂ̓���P�[�X�͏������@
b'2-4ac=0�@�@�������@�������@�u�iX�{�ʁj2 ���萔�A
�iY�{�ρj2���萔�v�@�Ƃ����`�ɂȂ����Ƃ��A����P�[�X�ł���B
�Ȃ��A�@�u�萔���O�@���������������݂��Ȃ��A�@�萔���O�@���ʂ��钼���A�@�萔���O�@���s����2�����@�v�@
�@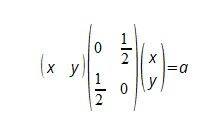
�Ώ̎���45�x��]���Ƃ킩�邪�A���s�ړ��s�v�̌`�� ��2�|(1/2)2���O�@�@
�ŗL�l���}1/2������ �@1/2�EX2�|1/2�EY2�@=�@a�@�@�Ƃ����`�ł���̂������o��
x2-xy-x�{y+1��x(x-y)-(x-y)+1=(x-1)(x-y)+1=�O�@
���s�ړ��̃��A�������߂�� q=(-1/2,1/2)�Ɖ��LA�̋t�s��@�|�P�A�|�P�ɂȂ�@���@���@x-1�Ay�@���@y-1�@�������́@�@���@���@x+1�@�Ay�@���@y+1�@�Ƃ����u���ŕ��s�ړ�
���̂Ƃ��@��q|A-1|q�����O�@�ƂȂ�@�萔���������Ȃ��A
�@X2-XY+1���O�@�@
�ȉ��̂悤�ɁA�@�����܂ʼn�]�ɂ��Ȑ��̕���(�@X2-XY�@�̕�������@�w�x�����Ȃ������Ɓj�ɏd���������Ă���Ă݂��
�������ɂȂ�Ƃ��́A�ŗL�l�̕Е����O�ƂȂ��āA����悩y��悪�������B
��1��2=ac-b2���O�@�ƂȂ��Ă��邩��A�����炭�͂�
�ʓ|�������ꎟ�̍���cos,sin�̌v�Z�ɂ��ĕ������̃P�[�X�ɂ����Ă͎���
cos2�Ɓ�{a/(a+c)}=32/50=16/25�@�@�@�@sin2�Ɓ�{c/(a+c)��18/50��9/25�@�Ƃ���ā@
�W��b�����Ȃ̂� cos�Ƃ�sin�Ƃ����Ƃ����邩��@4/5��3/5�ƂȂ�B
�����ЂƂ�,�ȉ~�ɂȂ��������Ă݂悤�B
�ʓ|�������ꎟ�̍���cos,sin�̌v�Z�ɂ���
����͐�ɕ��s�ړ����Ă����ƁA�������Ɉꎟ�̍���������B��q|A-1|q����125�@�@��q|A-1|q���|����125-25=100�A
����ČŗL�l����@�@100X2+25Y2=100 ,�@�@�S�̂��P�O�O�Ŋ��邾���ł���@�@�@ X2+Y2/4�@=1
�ȒP�ȍs��A�̌ŗL�l�́A���Ƃ��ǂ�Ȃ��̂��낤�B
�ȉ��̂悤�ȓ���Ȉꎟ�ϊ��ɂ́A�ŗL�l�̘b�͂ǂ��ł��������ƂȂ̂�������Ȃ��B�����ς��Ȃ��Ƃ��p�x������邾���Ƃ��B
- �P�ʍs������@��=1�����ł���B�ŗL�x�N�g���͓��ɂȂ��B
- ��]�̍s�ƁA�Ȃ�ƕ��f���@�Ɂ�cos�Ɓ}i�Esin�Ɓ@����͊������]��\���s��ɑΉ����镡�f���ł���B�����ʂŌŗL�x�N�g���͑��݂��Ȃ��B
- �������W�����ւ���s��Ƃ��A���[�����c�ϊ��icosh�ƁAsinh�Ƃ̑Ώ̍s��j�́A�ŗL�x�N�g���̌��ʂƂ��Ă��A�@y�����@�Ɓ@y=-x�@��������������ȕ����ł���B
�Ɂ��}�P�@����с@�Ɂ����}�Ɓ@�ȂǂƂ����Q�̌ŗL�l�������Ƃ���B ��1��2�@���l�͍s�ƈ�v����B
���Ƃ��Ƃ̒�`�������
�ŗL�x�N�g��������Ȃ�A�����̈ꎟ�ϊ��`�����ĎΌ����W�n�Ɉڂ��Ă��ς��Ȃ����ʂȍ��W����������Ƃ������Ƃł���B
���̂悤�Ȉꎟ�ϊ�A�̍s����ꍇ�A���̍s��A�̓������������̂ł���B
��������]�̈ꎟ�ϊ��ł́A���̂悤�ȕ����͌�����Ȃ����낤�B���ׂĉ���Ă��܂�����B
�ŗL�x�N�g���Q�̗�łł���P�Ƃ����s��́A���̓�����������W�n�̂Q���Ƃ���Ό����W�ֈڂ����߂̈ꎟ�ϊ��̍s��Ƃ��ăC���[�W�ł��邾�낤�B
�ŗL�l�ƌŗL�x�N�g�������܂�Ƃ��A�Ȃɂ��֗��Ȃ��Ƃ͂��邩�B�����A��Ίp���ł��āA���̑Ίp�s��̐ς��ȒP�ł��邱�Ƃɂ��B
�ݏ�̌v�Z�͓��ɊȒP�Ȃ̂ł���B