 1次変換と座標軸
1次変換と座標軸  1次変換と座標軸
1次変換と座標軸
たまたま、一次変換の慣習的には、列ベクトル採用とみてよい。
一次変換も列ベクトルを基本扱うが、単に慣習である。
行と列を入れ替えた場合(転置行列)は、積の順序が変わる。
列ベクトルであらわされる座標 => 行列Aの列ベクトルの座標軸に置き換え
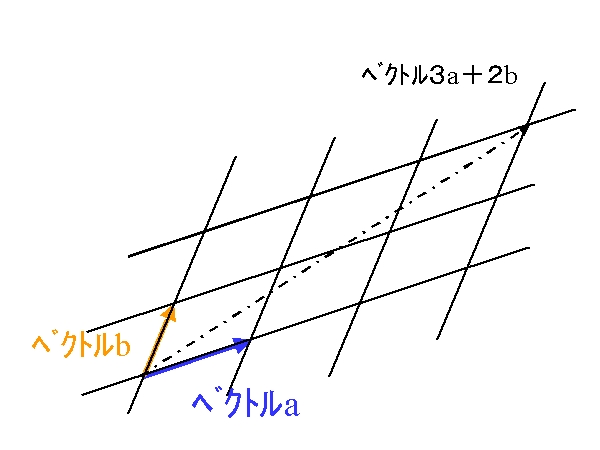
もとをデカルト座標の点(p,q)だとしたら、 ベクトルa,bでつくる斜交座標の格子点(p,q)に移ったと見られる
具体的にはデカルト座標点(p,q)=(3,2)なら、1次変換行列をAとしてベクトル表現で、1次変換のA行列により平面の点が以下のような位置に移る。
例えば変換元が (p,q)=(3,2)なら
A
3ex+2ey → 3a+2b 単位ベクトルがAの列ベクトルaとbに置換された格好になるわけだ。
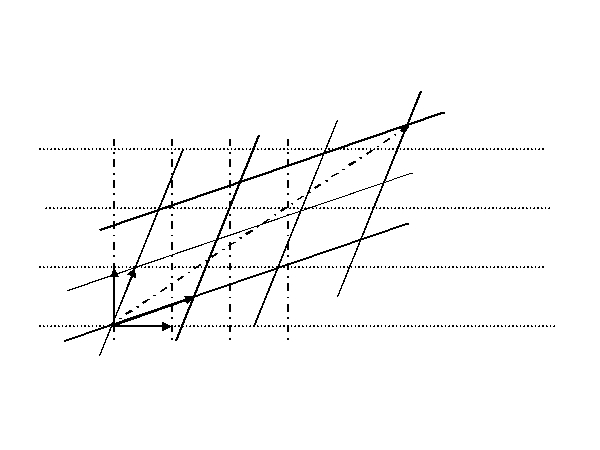
3次元なら以下のようになる

デカルト座標の升目が面積1×1の正方形だったり、体積1×1×1の立方体であるのが、
新座標では平行四辺形の面積や平行六面体の体積となるとき、それは行列式がその大きさを表している。
単位ベクトル(1,0)と(0,1)がAの列ベクトルだったら、単位行列Eとなる。
単位行列って、単位ベクトルを並べた行列ってことだな。
ex ey
↓ ↓
| 1 |
0 |
| 0 | 1 |
1次変換行列としても、変換先の座標軸であるベクトルが、ex 、ey だから、下記のように元の点と一致するだけである。
E
3ex+2ey → 3ex+2ey
行の視点で見ても同じ、慣例的に列分割を一次変換に使っているにすぎない。
行ベクトル系に転置した行列も「同じ座標系変換」を表し、行列を転置しても行列式は同じ。
また、また余因子展開の仕方、スカラー3重積、ともに行ベクトル視点で計算しても行列式は同じ。
以下の3×3行列の積は、AXB=C は 2つの見方ができる。この積は、3つの座標点を同時に一次変換しているものとみる。
行列A、 行列B、 行列C, 3行ベクトルx3列ベクトルで内積が9通り
| x |
|
b1ex |
|
= |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| b2ey | ||||||||||
|
a1ex |
a2ey |
a3ez |
|
b3ez |
|
a・b |
|
列ベクトル視点:
行列Bの列ベクトル3つの各座標を行列Aの列ベクトルを座標軸とする点に変換、結果は、行列Cの列ベクトル
行ベクトル視点
行列Aの行ベクトル3つの各座標を行列Bの行ベクトルを座標軸とする点に変換、結果は、行列Cの行ベクトル
※行ベクトル視点の方が、流れが美しいかも、AがBを通じてCになる。
![]() 行列式の幾何学的なイメージ
行列式の幾何学的なイメージ
外積と高校の2次の正方行列の行列式ad-bcは似ているだろう?
a×b= (a2b3-a3b2)ex+(a3b1-a1b3)ey+(a1b2-a2b1)ez
上の各成分は、2次の正方行列、いわゆる高校で最初に習う2行2列の行列(2×2行列)の成分a,b,c,dで行列式を求めると「ad-bc」となるというのによく似ているんですね。
2x2行列のad-bcという値は3次元に拡張した空間の中でxy平面上の2つのベクトルの外積
2X2行列式は、斜交座表系の単位面積(平行四辺形)に変換された新しい座標系における
面積拡大縮小率に関連している。
行列式が0となるときは、一次変換後に次元が縮退(ランクが下がる)
座標軸を表すベクトル方向に独立していないものがある。(あるベクトルが別のベクトルのスカラー倍や一次結合となってしまう)
2次でも3次の場合は、外積やスカラー3重積をイメージすればわかるだろう
正方行列の列ベクトル(変換後の座標軸)に、
・0ベクトルがある。 (座標軸が1つ縮退)
・2つのベクトルで作る平行四辺形の面積が0、外積が0。(ベクトルが平行だから1つ座標軸方向の意味しか持たない、次元が縮退)
・外積が0にならない場合、残りのベクトルとの内積が0 (3次正方行列で、ベクトルが同一平面にあるから変換後は2次元に閉じ込められて、次元縮退)
3次の場合、3つとも平行だったら1次元になるし、一平面の場合もあるし、高次の場合は、縮退程度はいくつもあるということだ。
線形代数で習うのは、変換後の次元を「行列のランク」と呼んでいるのだ。次元が縮退したらランクが下がるのだ。
ベクトルが一次独立していない。
あるベクトルが、別のベクトルの一次結合で表せてしまうということだ。次元的に軸としての意味のないベクトルが存在することになる。
2x2行列 2つの列ベクトルでつくる 平行四辺形の大きさ:Sは
1.内積の定義から
a =(a,c) ,b=(b,d) 2つのベクトルのなす角をθとすると S=|a|・|b|・sinθ
S2=|a|2・|b|2・sin2θ=|a|2・|b|2(1-cos2θ)= |a|2・|b|2-(|a|・|b|cosθ)2
|a|2・|b|2=(a2+c2)(b2+d2) および (|a|・|b|cosθ)2=(a・b)2=(ab+cd)2 なので S2=(a2+c2)(b2+d2)-(ab+cd)2=(ad-bc)2
∴ S=|ad-bc|
(a,c)(b,d)で列ベクトルから2次の正方行列Aをつくったとき Aの行列式|A|=ad-bcであるから、この行列式の大きさが平行四辺形の大きさである
2.三角関数の加法定理から
a =(a,c) ,b=(b,d) それぞれのベクトルの偏角(X軸の正方向を基準にした角)を α、β とする
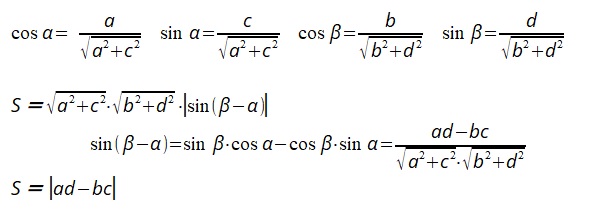
3.行列の公式で、以下の3点の性質でも、ただちにわかる。
(A) 行列の積は、行ベクトルと列ベクトルの内積である。
(B) 行と列をいれかえた転置行列の行列式も,もとの行列と同じ値である。 |A|=|tA|
(C) 積の行列の行列式=それぞれの行列式の積に等しい。 |tA・A|=|A|・|tA|=|A|2
4.外積の定義からは、ただちに
XY平面上の成分同士の外積=>Z成分 YZ平面上の結果⇒X成分、ZX平面上の結果⇒Y成分
2次元のベクトル(a,c)(b,d)を3次元で見ると、 a ×b=(a,c,0)×(b,d,0)=(0,0,ad-bc)
XY面上のベクトルの外積なので、2つのベクトルでつくる平行四辺形の大きさで、Z方向ベクトルとなる。
行列式ad-bcは、「2つのベクトルでできる平行四辺形の大きさ」ということがわかる(正か負か符号は別として)。
2次元での行列式の正・負はなんの違いなのか
平面に表裏があるので、一次変換の結果が、右手の親指と人さし指の付き方がそのまま変わらないのと、左手のように変わってしまうのと2通りある。そのうち、変わらないのが正だと思っておけばいい。
負になるケースでは、どちらかの手のひらを表裏をひっくり返えさないかぎり軸を合わせることはできないのである。
3次元での行列式の正・負は
「フレミングの左手の法則と同じ格好の右手で親指をx軸とするとy人指し指で、zが中指というのが慣習上よく使われる軸である。しかし左の方では軸の付きかたが違うことになる。空間的な構造で四面体構造のメタン形化合物に鏡面対称の2つのパターンがあるのと同様である。これが行列式の正か負を決める。右手系から左手系に違う軸の付きかたに変換されたら負である」
平行六面体の体積と3次元での行列式
x、y、zと同じ方向でa、b、c系があれば、
aとbで外積をとると、aとbの平行四辺形の大きさを持ち、四辺形の面に垂直方向のベクトルができる。
これとcとで内積をとると,平行六面体の体積である。この式は、スカラー3重積で、3次正方行列の行列式とも一致する。
この結果は、2次で平行四辺形であったのが、3次では六面体になったのである。ただし、ベクトルの軸のつきかたにより、値は負になる。
回転の行列
デカルト座標に似たもの、大きさ1で直交する座標系(正規直交系)に移す変換のひとつは、
回転の行列が代表的なものの1つである。
複素数は掛け算すると、複素平面上で偏角だけ回転させ、大きさは絶対値倍となる性質から、これと親密な関係にある。
一般的な角度θで座標軸回転を見てみると、単位円上で2つの直交ベクトルを座標軸ベクトルと想定すればいい。2つの列ベクトルは直交しているから、成分を入れ替えて一方がマイナス符号という形であるはずだ。
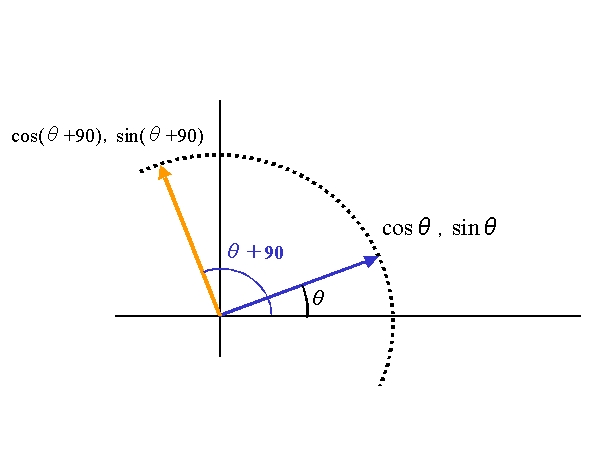
単位円上の点
a=( cosθ,sinθ)なら、直交しているベクトルbはθのかわりにθ+90度にすればよい。
b=( cos(θ+90°),sin(θ+90°))--->(-sinθ,cosθ)
したがって一次変換の 2×2行列は以下で、この行列式は1(cosの2乗+sinの2乗=1)で、軸の関係は素直で折り返していない。
もちろん極座標と加法定理を使えば、同様に回転行列が求まる
原点からの距離rで偏角φの座標をθだけ回転させたら、もとの座標をx,yとしてx=rcosφ,y=rsinφ となる。
θ回転後の座標X、Yとすると、下記のごとく加法定理からx、yに相当する上記で整理して、xとyの1次式になる。
X=rcos(θ+φ)=r(cosθcosφ-sinθsinφ)=cosθrcosφ-sinθrsinφ
Y=rsin(θ+φ)=r(sinθcosφ+cosθsinφ)=sinθrcosφ+cosθrsinφ
ここで、x=rcosφ,y=rsinφ であるから以下になる。
X=cosθ・x-sinθ・y .......(A)
Y=sinθ・x+cosθ・y .......(B)
複素平面を使って回転を考えてもよい
ドモアブルの定理だ。
複素数の掛け算が偏角の加法であるということ、すなわち、絶対値1である複素数をかければ偏角だけ回転ができる。
これは、複素数の行列表現と関係してくる。回転の行列とは絶対値1の複素数と同様なのである。
x+iyという複素数なら、これは座標(x、y)である。これにcosθ+i・sinθという複素数をかけるとθだけ回転させることになるから
x、y → X,Y に移るとすると 座標点である(実部と虚部)がどうなるかを見る
(x+iy)×(cosθ+i・sinθ)= (cosθ・x-sinθ・y)+i(sinθ・x+cosθ・y)= X + iY
ここで、実部と虚部を比較すればよい。結果(A)(B)と同じである。
X=cosθ・x-sinθ・y
Y=sinθ・x+cosθ・y
これらは、内積で表せるが、内積のかける順番の仕方で2通りの行列の形に表現される。
行ベクトルのような横書きもいいのである。
行と列を入れ替えた場合(転置行列)は、積の順序が変わる。
(x、y)-->(X、Y)のθ回転の1次変換の式に。列ベクトルで表現しても行ベクトルで表現してもよいが、通常は列ベクトルが使われる。
下記のような式の左辺には、このように表現は両方あったほうがいい。

「互いに直交する」2つの列ベクトルを想定しても回転の行列の形は自然と出てくる。ただ回転ではないやつ もいる。
以下のように 複素数は、2x2回転行列のスカラー倍と表現されうる。

少し行列式が正か負かという、とても単純な成分でできた行列を見てみよう
行列式が正となるのは、回転の行列である。0度(単位行列)、+90度、-90度、±180度
これらは座標軸の付き方が変わらない(折り返さない:平面が裏返しにならない)ものである。
90度の回転:
虚数iをかけると90度複素平面で回転するのと似ている。
二乗すると180度回転
になり、単位行列の(スカラー)-1倍で、iを二乗すると-1になるのと似ている。
複素数の表現行列とは、
単位行列(=Eとする), 90度回転行列(=Iとする)の一次結合
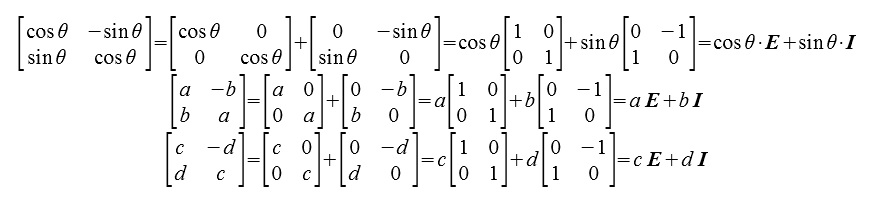
cosθE+sinθI
これはオイラーの式に出てくる複素数の行列表現である。「絶対値が1で偏角θの複素数: cosθ・1+sinθ・i 」をかけること ⇒ 複素平面上でθだけ回転する。
ある複素数(2元数)に、a+biなんていう複素数を掛け算すると、この複素数の絶対値スカラー倍し偏角が加わることになるが
前に説明した2x2行列では回転の行列と同じ形をしていて、行列の積が複素数の掛け算の効果を持っている。
aE+bI という形の行列で、前に記載した列ベクトル同士が直交するような行列の形である。
aE+bI という形の行列で、行列式は複素数の絶対値であり、スカラー0は、行列式=0のときである。
すなわち0に逆数が存在しないのと、逆行列が存在しないのと、一致している。
複素数の表現行列の固有値は。
なんと、そのまんま複素数が出るというね。

複素数(2元数)だけでなく 4元数の行列表現 それはこちらのリンクへ
合成写像の例
ある点(x,y)を 90度回転して、y軸対称をする、それはxとyの入れ替え(y=xに対称)となる。
それは一次変換の結合、すなわち行列の積をみればわかる。
±90度回転は、y=xに対称な点に移す(x、yの座標入れ替え)と似てるが、成分の一方が負になる。
三角関数の加法定理と回転の合成
φの回転行列と結合、三角関数の加法定理から、θ+φの場合になっていることがわかる。
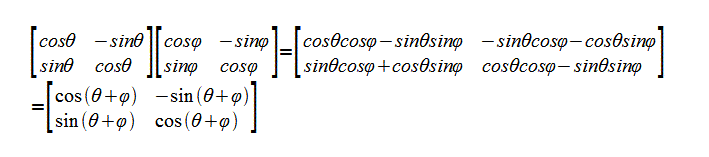
あとで特殊相対論のローレンツ変換が一次変換行列だなんて出てくるんですが、
双曲線関数:ハイパブリックsin、cos (coh,sinh)の成分である。
=>1次変換としてのローレンツ変換のリンク
行列式=1となるような双曲線関数の行列は、右上の成分だけマイナス符号がつかないし、加法定理も正負の複号が同順で
「ひねくれた」ところがない。
複素数(2元数)だけでなく、4元数の行列表現もある
回転して、2次曲線を分類してみる それはこちら
1次変換と特殊相対論へいきます
前のページ
http://www.ne.jp/asahi/imaimai/homepage/ indexに戻る