シミュレーションで明らかなように,5個のラグランジュ点のうち,点 L1 ~ L3 は非常に不安定であり,人工衛星がこれらの位置から少しでもずれると,そのずれはますます増大していってしまいます。これに対してラグランジュ点 L4と L5 は安定しており,人工衛星がこれらの点から多少ずれても大きくずれていくことはありません。
このことは,先に示した $XY$ 座標系に対する運動方程式 $\maru{2}$ 式を使って導かれるのですが簡単ではありませんので,本稿では深入りせず定性的な説明にとどめます(多少乱暴な説明になっているかもしれません)。
◎ゼロ速度曲線:
先の運動方程式より,\[m \Vec{a} = m \dif{ \Vec{v}}{t} = \Vec{f} + m \omega_0{}^2 \Vec{r} + 2m[\Vec{v} \times \Vec{\omega_0} ] \quad \cdots\cdots\maru{2}\]
上式に速度 $\Vec{v}$ を内積として乗じると,
\[ m \Vec{v}\dif{ \Vec{v}}{t} = \Vec{f}\cdot\Vec{v} + m \omega_0{}^2 \Vec{r}\cdot \Vec{v} + 2m \Vec{v}\cdot [\Vec{v} \times \Vec{\omega_0} ] \\ \kern-1em \therefore \bun{\mathrm{d}}{\mathrm{d}t}\bigg(\bun{1}{2}m \Vec{v}^2\bigg) = \Vec{f} \cdot \dif{\Vec{r}}{t} + m \omega_0{}^2 \Vec{r}\cdot \dif{\Vec{r}}{t} + 2m \Vec{v}\cdot [\Vec{v} \times \Vec{\omega_0} ] \\ \kern7em = \Vec{f} \cdot \dif{\Vec{r}}{t} + \bun{\mathrm{d}}{\mathrm{d}t}\bigg(\bun{1}{2}m \omega_0{}^2 \,\Vec{r}^2\bigg) + 2m \, \Vec{\omega_0}\cdot [\Vec{v} \times \Vec{v} ]\]
右辺第3項の式変形には, $\Vec{A}\cdot [\Vec{B}\times \Vec{C}] = \Vec{C}\cdot[\Vec{A}\times \Vec{B}]$ の関係を使ってベクトルの順序を入れ替えた。
ここで同じベクトルの外積はゼロゆえ, $[\Vec{v}\times \Vec{v}] = 0$ であり,また同じベクトルの内積 $\Vec{A}\cdot\Vec{A} = A^2$ ですから,上式は次式のように簡単化されます。\[\bun{\mathrm{d}}{\mathrm{d}t}\bigg(\bun{1}{2}m v^2\bigg) - \Vec{f} \cdot \dif{\Vec{r}}{t} - \bun{\mathrm{d}}{\mathrm{d}t}\bigg(\bun{1}{2}m \omega_0{}^2 \,r^2\bigg) = 0 \]
さらに上式を時間積分すると,\[\bun{1}{2}m v^2 - \int \Vec{f}\cdot \mathrm{d}\Vec{r} - \bun{1}{2}m \omega_0{}^2 r^2 = const. \]
よって\[\phi = - \int \Vec{f}\cdot \mathrm{d}\Vec{r} - \bun{1}{2}m \omega_0{}^2 r^2 \quad \cdots\cdots\maru{7} \]
とおくと,\[\bun{1}{2}m v^2 + \phi = const. \]
となり,運動エネルギーと $\phi$ の和が一定に保たれることになります。
これは $XY$ 座標系における人工衛星の力学的エネルギー保存則に相当するもので,本問のような3対問題を考えるときにきわめて重要な保存量となります(ヤコビ積分)。
$\phi$ は万有引力と遠心力との合力による一種のポテンシャルのような意味合いを持つ量で,下図は,$\phi$ についての等高線を表します。この等高線(グラフ)のことをを ゼロ速度曲線と言います(下右図は,これに高低を模式的に付加したものです)。
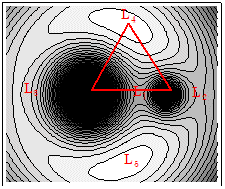
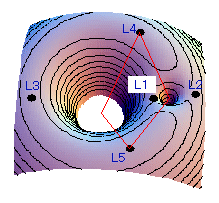
ポテンシャル面の傾きは力を表しますので, $XY$ 座標系において人工衛星はこのポテンシャル面が傾いている方向・向きに力を受けることになります。したがって,等高線の峰より地球もしくは月の方に傾いている位置ではそれぞれの引力が強く働くところであり,峰より外側に傾いているところでは遠心力が強いことを意味します。ラグランジュ点は,$\phi$ がちょうど極大値をとる位置に相当します。
◎ラグランジュ点の安定性について :
ここで人工衛星がある点から動き出したとすると, 座標系において力学的エネルギーが保存されることから, $\phi$ の小さいところ(上図の色の濃い部分)に行くほど,人工衛星の運動エネルギーが増大し,速度が増大していくことになります。ところが $XY$ 座標系内で運動する物体にはコリオリの力が働きます。ここが重要ポイントです。
$XY$ 座標系が反時計回りに回転している場合, コリオリの力は速度 $\Vec{v}$ に直角で進行方向に対して右向きに働きます(コリオリ力の項を参照してください)。
まずラグランジュ点L4付近の運動について考えてみましょう。
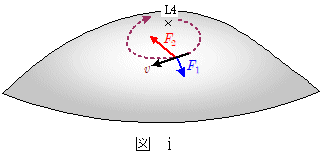
図ⅰを見てください。L4点からほんの少しずれた位置に人工衛星があって,人工衛星が $\phi$ 面の勾配の向きに力を受けて動き始めたとします。ラグランジュ点L4付近では $\phi$ 面の勾配は極めて緩やかになっているため,人工衛星に働く $\phi$ 面の勾配による力(万有引力と遠心力との合力) $F_1$ (上図参照)はかなり小さくなっています。一方,L4点から離れるにつれて人工衛星の速度は徐々に増していくことになりますが,このとき働くコリオリの力 $F_2$ の方が $F_1$ に勝れば,人工衛星は向きを変えて再びL4点の方に引き返していくことになります。以後この繰り返しによって,人工衛星はL4点付近でウロウロすることになる…というわけです。
つぎに,L1,L2,L3点付近での衛星の動きについて考えてみましょう。
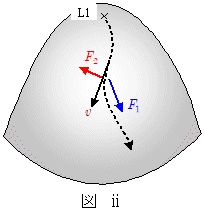
L1,L2,L3点付近では $\phi$ 面は極めて急勾配になっています。したがって $\phi$ 面の勾配による力 $F_1$ は大きく,コリオリの力 $F_2$ が働いているにもかかわらず軌道は曲がりきれず,どんどんL1,L2,L3点から離れていってしまう…というわけです。
この辺の事情は,スキーでカーブをしようとエッジを立てているとき,緩斜面なら曲がりきれて元の位置に戻ってこられるが,急斜面ではエッジを立てているにもかかわらずどんどん下方に滑り落ちていく……といった感じに似ているかもしれません。
*********
以上より分かるように,ラグランジュ点の安定性については $\phi$ 面の勾配が重要な鍵を握っており,これは「地球と月」といった元になる2天体の質量比で決まります。
詳しい計算によれば,2天体のうち質量の小さい方が大きい方の質量の $\bun{9-\kon{69}}{9+\kon{69}}\kinji 0.040$ 倍以下であるとき,L4,L5点は安定な平衡点になることが分かっています。前ページに掲げた表より,地球と月の場合も,太陽と地球の場合もL4,L5点は安定な平衡点であることが分かります。質量比がこれを満たさないときは,たとえ正三角形解の位置であっても安定性はないことになります。