ラグランジュ点は,人工衛星に働く万有引力の合力と遠心力との平衡点(つり合い点)です。
人工衛星が共通重心Gのまわりを角速度 $\omega_0$ で周回するとき,人工衛星に働く遠心力は重心Gと人工衛星を結ぶ方向で外向きですから,この遠心力とつりあうためには万有引力の合力 $\Vec{f}$ は重心Gの方向に向いていなくてはなりません。このような点として,地球と月を結ぶ直線上にある点と,この直線上にない点に分けて考えることができます。
◎直線平衡解:
下図のように,地球・月を結ぶ直線上にあるラグランジュ点(L1,L2,L3)について考えます。
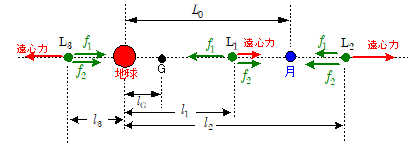
1.ラグランジュ点 $\mathrm{L_1}$ :
地球と月の間にある $\mathrm{L}_1$ 点について。
この位置では,上図において,地球からの引力 $\Vec{f}_1$ は左向き,月からの引力 $\Vec{f_2}$ は右向き,遠心力は右向きに働きます。 よって前ページの $\maru{3}$ 式より, $\mathrm{L}_1$ 点の地球からの距離 $l_1$ は,次式を満たします。 $\omega_0$ は前ページの $\maru{1}$ 式で与えられます。\[0 = -f_1 + f_2 + 遠心力 \\ \quad = -\bun{G m M_1}{l_1{}^2} + \bun{G m M_2}{(L_0 -l_1)^2} + m \omega_0{}^2 (l_1 - l_\mathrm{G}) \\ \quad = -\bun{G m M_1}{l_1{}^2} + \bun{G m M_2}{(L_0 -l_1)^2} + m\bigg( \kon{\bun{G (M_1 + M_2)}{L_0{}^3}}\, \bigg)^2 \bigg(l_1 - \bun{M_2}{M_1 + M_2}L_0 \bigg) \quad \cdots\cdots\maru{4} \]
2.ラグランジュ点 $\mathrm{L_2}$ :
地球-月-人工衛星 の順に並んだ $\mathrm{L}_2$ 点について。
上図を参照にして,\[0 = -f_1 - f_2 + 遠心力 \\ \quad = -\bun{G m M_1}{l_2{}^2} - \bun{G m M_2}{(l_2 - L_0 )^2} + m \omega_0{}^2 (l_2 - l_\mathrm{G}) \\ \quad = -\bun{G m M_1}{l_2{}^2} + \bun{G m M_2}{(l_2 - L_0 )^2} + m\bigg( \kon{\bun{G (M_1 + M_2)}{L_0{}^3}}\, \bigg)^2 \bigg(l_2 - \bun{M_2}{M_1 + M_2}L_0 \bigg) \quad \cdots\cdots\maru{5} \]
3.ラグランジュ点 $\mathrm{L_3}$ :
人工衛星-地球-月 の順に並んだ $\mathrm{L}_3$ 点について。
\[0 = f_1 + f_2 - 遠心力 \\ \quad = \bun{G m M_1}{l_3{}^2} + \bun{G m M_2}{(l_3 + L_0 )^2} - m \omega_0{}^2 (l_3 + l_\mathrm{G}) \\ \quad = \bun{G m M_1}{l_3{}^2} + \bun{G m M_2}{(l_3 + L_0 )^2} - m\bigg( \kon{\bun{G (M_1 + M_2)}{L_0{}^3}}\, \bigg)^2 \bigg(l_3 + \bun{M_2}{M_1 + M_2}L_0 \bigg) \quad \cdots\cdots\maru{6} \]
以上 $\maru{4}$ ~ $\maru{6}$ の3式はそれぞれ $l_1$ , $l_2$ , $l_3$ に関して5次方程式になるので,一般的な形では解を求めることはできませんが,近似的な数値解なら計算することができます。 以下にいくつかの例についてラグランジュ点 $l_1$ , $l_2$ , $l_3$ の値を示します。
| 天 体 | 質量比 $M_2/M_1$ | 距離 $L_0$ | $l_1$ | $l_2$ | $l_3$ |
| 月/地球 | $0.0123$ | $3.84\times 10^5\mathrm{km}$ | $0.849L_0$ | $1.168L_0$ | $0.993L_0$ |
| 地球/太陽 | $3.04\times 10^{-6}$ | $1.5\times 10^8\mathrm{km}$ | $0.990L_0$ | $1.010L_0$ | $1.000L_0$ |
| 木星/太陽 | $9.55\times 10^{-4}$ | $7.8\times 10^8\mathrm{km}$ | $0.933L_0$ | $1.070L_0$ | $0.999L_0$ |
◎正三角形平衡解:
地球・月のライン上にない平衡点としては,地球・月・人工衛星の3者が正三角形をなす位置のみとなります。
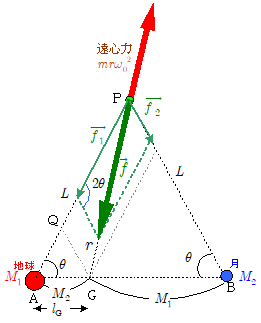
万有引力の合力 が共通重心Gに向くためには,まず△PABは2等辺三角形でなければなりません。以下にこれを示します。
上図において, $\overline{\mathrm{AP}} = \overline{\mathrm{BP}} = L$ とします。
もし△PABが2等辺三角形であるとすれば, $\mathrm{PB}$ に平行に $\mathrm{QG}$ をとったとすると,2等辺三角形の相似の関係から, $\overline{\mathrm{AG}} : \overline{\mathrm{GB}} = \overline{\mathrm{AQ}} : \overline{\mathrm{QP}}$ ,かつ $\overline{\mathrm{AQ}} = \overline{\mathrm{QG}}$ なので,\[\bun{\overline{\mathrm{AG}}}{\overline{\mathrm{BG}}} = \bun{\overline{\mathrm{AQ}}}{\overline{\mathrm{QP}}} = \bun{\overline{\mathrm{QG}}}{\overline{\mathrm{QP}}} \\ \kern6em = \bun{f_2}{f_1} \\ \kern 6em = \bun{\,\,\,\bun{G m M_2}{L^2}\,\,\,}{\bun{G m M_1}{L^2}} \\ \kern 6em = \bun{M_2}{M_1} \]
AB間を $M_2:M_1$ の比に内分する点は,まさに地球と月の共通重心にほかなりません。すなわち万有引力の合力が地球と月の共通重心Gに向くためには,まず△PABが2等辺三角形であればよいことになります。
つぎに△PABが正三角形であるとき,人工衛星に働く遠心力の大きさが万有引力の合力 $\Vec{f}$ の大きさに等しくなることを示します。
$\overline{\mathrm{AP}}$ と $\overline{\mathrm{BP}}$ が地球・月間の距離 $L_0$ に等しく( $\overline{\mathrm{AP}} = \overline{\mathrm{BP}} = \overline{\mathrm{AB}}=L_0$ ),かつ上図で $\theta = 60^\circ$ とすると,\[\kern-2em 万有引力 \\
f = \kon{f_1{}^2 + f_2{}^2 - 2f_1\,f_2\,\cos 2\theta} \\ \quad = \kon{\bigg(\bun{G m M_1}{L_0{}^2}\bigg)^2 + \bigg(\bun{G m M_2}{L_0{}^2}\bigg)^2 - 2\bun{G m M_1}{L_0{}^2}\bun{G m M_2}{L_0{}^2} \times \cos120^\circ } \\ \quad = \bun{G m}{L_0{}^2}\kon{M_1{}^2 + M_2{}^2 + M_1 M_2} \\[1.5em] \\ \kern-2em 遠心力 \\
m \, \omega_0{}^2 \times \overline{\mathrm{PG}} = m\bigg(\kon{\bun{G(M_1 + M_2)}{L_0{}^3}}\bigg)^2 \kon{\overline{\mathrm{AP}}{}^2 + l_\mathrm{G}{}^2 -2\overline{\mathrm{AP}} \cdot l_ \mathrm{G} \times \cos 60^\circ} \\ \kern2em = \bun{G m (M_1 + M_2)}{L_0{}^3} \kon{L_0{}^2 + \bigg(\bun{M_2}{M_1 + M_2}L_0\bigg)^2 - L_0\cdot \bun{M_2}{M_1 +M_2}L_0 } \\ \\ \kern2em = \bun{G m}{L_0{}^2} \kon{M_1{}^2 + M_2{}^2 + M_1 M_2} \\ \kern -1em \therefore f = m \omega_0{}^2 \, r \]
すなわち△PABが正三角形であるとき,この点Pで万有引力の合力と遠心力とがつりあうことになります。
(以上のほかに,ごく最近,3体の質量が等しい場合について,3体が8の字上を「追っかけっこ」をするように運動する「8の字解」があることが発見されました。)
次に,ラグランジュ点の安定性について説明します。
詳解3(ラグランジュ点の安定性)に続く。