以下,『円制限三体問』について解説します。
『円制限三体問』は,3体問題(3つの物体からなる系の力学問題)のうち,3つ目の物体の質量が他の2体に比べて十分小さく,重い方の2体の共通重心の周りを3体が同じ周期で円運動をする…というものです。
以下では,3体は 地球・月・人工衛星 であるとし,人工衛星が地球と月の引力を受けながらその共通重心のまわりを周回するという設定で説明していきます。これら3体の大きさは無視し,質点として扱います。
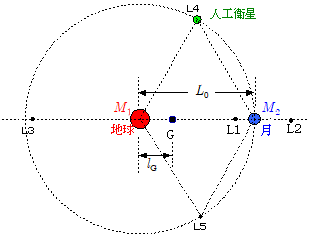
まず,3体が重心Gの周りを回転する角速度 $\omega_0$ を求めます。
人工衛星の質量は地球や月に対して無視できるので,全体の共通重心Gは地球と月だけで決まります。
地球・月間の距離を $L_0$ ,それぞれの質量を $M_1$ , $M_2$ とすると,2質点と重心との距離は質量に反比例することから,地球から重心Gまでの距離 $l_\mathrm{G}$ は,\[l_\mathrm{G} = \bun{M_2}{M_1 + M_2}L_0 \]
よって地球(または月)について円運動の式を立てることによって,地球・月の公転角速度 $\omega_0$ を求めることができます。
万有引力定数を $G$ として,地球について円運動の式を立てると,\[M_1 \times 向心加速度 = 地球に働く万有引力 \\ \kern-1em \therefore M_1 \, l_\mathrm{G} \, \omega_0{}^2 = \bun{G \,M_1\, M_2}{L_0{}^2} \\ \kern-1em \therefore M_1 \cdot \bun{M_2}{M_1 + M_2}L_0 \cdot \omega_0{}^2 = \bun{G \,M_1\, M_2}{L_0{}^2} \\ \kern-1em \therefore \omega_0 = \kon{\bun{G (M_1 + M_2)}{L_0{}^3}} \quad \cdots\cdots\maru{1} \]
地球と月は人工衛星の動きに関係なく地球・月の重心Gの周りに角速度 $\omega_0$ で等速円運動を続けているのですから,人工衛星については地球・月に対する相対運動について考えれば十分です。
以下,地球・月に固定した座標系(以後, $XY$ 座標系と呼ぶ)を考えると,人工衛星の相対運動はこの $XY$ 座標系内での運動 ということになります。
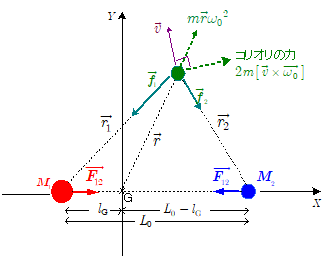
この 座標系は一定角速度 $\omega_0$ で回転する回転座標系ですので,人工衛星に働く力としては地球・月からの万有引力のほかに,座標の回転に伴う遠心力と コリオリの力を考える必要があります。ここで遠心力もコリオリの力も,回転座標系で観測した場合に現れる慣性力です。したがって人工衛星の $XY$ 座標系内での加速度を $\Vec{a}$ とすると,人工衛星の $XY$ 座標系内での運動方程式は,上図の文字を使って,\[m \Vec{a} = \Vec{f_1} + \Vec{f_2} + m \, \omega_0{}^2 \Vec{r} + 2m[\Vec{v} \times \Vec{\omega_0} ] \\ \quad = \Vec{f} + m \omega_0{}^2 \Vec{r} + 2m[\Vec{v} \times \Vec{\omega_0} ] \quad \cdots\cdots\maru{2}\]
上式の右辺第1項 $\Vec{f}$ は地球・月からの万有引力の合力,第2項 $ m \, \omega_0{}^2 \Vec{r} $ は遠心力,第3項 $2m[\Vec{v} \times \Vec{\omega_0} ]$ はコリオリの力です。ただし, $\Vec{v}$ は人工衛星の $XY$ 座標系内での速度であり,この座標系の回転角速度 $\Vec{\omega_0}$ の方向はこの面に垂直とします。 $[\Vec{v} \times \Vec{\omega_0} ]$ は $\Vec{v}$ と $\Vec{\omega_0}$ との外積(ベクトル積)を表し, $\Vec{v}$ ベクトルから $\Vec{\omega_0}$ ベクトルの向きに右ねじを回したときのねじの進む向きを向き,両ベクトルの直角成分の積を大きさに持つベクトルになります。
さて,人工衛星が共通重心の周りを地球・月とともに運動しているとすれば,人工衛星はこの座標系に対して静止していることになるので,その条件は上式で $\Vec{v} = 0$ ,かつ $\Vec{a} = 0$ を満たしていることになります。上式にこの条件を入れると,\[0 = \Vec{f} + m \omega_0{}^2 \Vec{r} \quad \cdots\cdots\maru{3} \]
つまり,人工衛星が地球・月とともに公転角速度 $\omega_0$ で共通重心Gのまわりを公転することのできる位置は,人工衛星に働く万有引力の合力と遠心力とがつりあう位置ということになります。この平衡点(つりあい点)のことを ラグランジュ・ポイント と言います。
次ページで,このラグランジュ点,すなわち万有引力と遠心力との平衡点(つりあい点)を求めます。
ラグランジュ点 詳解2 へ続く。