
このとき星Bについて,保存されれる物理量が2つあります。力学的エネルギーと面積速度です。
万有引力は保存力でなので,力学的エネルギーが保存されることは前述したとおりです。
また星Bにはたらく万有引力は常に恒星Aの方に向いています。このように力が常にある定点に向いており,かつ力の大きさが定点からの距離のみによって決まるような力を中心力と言います。物体にはたらく力が中心力の場合,面積速度(動径ベクトル $\Vec{r}$ が単位時間に描く面積。上図の青色で示した部分の面積 $S$ )は常に一定に保たれます。これを面積速度一定の法則といい,この法則を惑星の運動について述べたのがケプラーの第2法則です(面積速度一定の法則は角運動量保存の法則と同じ内容を持ちます)。
詳しい説明は「ブランコをこぐ」の物理的意味-3を参照してください。
上図において,星Bの速度 $\Vec{v}$ を,動径ベクトル $\Vec{r}$ 方向とこれに垂直な方向とに分解し,動径ベクトル方向成分を $v_\parallel$ ,動径ベクトルに垂直な方向成分を $v_\perp$ とすると,面積速度 $S$ は,\[S = \bun{1}{2}r \, v_\perp \]で与えられます。 よって星Bの力学的エネルギーを $E$ ,面積速度の2倍の値を $h$ とすれば,これら2つの値は常に一定値に保たれ,次式で表されます。\[ \left \{ \begin{array}{rl} & \kern-1em E = \bun{1}{2}m v^2 + U \\ & \kern-1em \quad = \bun{1}{2}m (v_\parallel{}^2 + v_\perp{}^2) - \bun{G M m}{r} \quad\cdots\cdots\maru{1} \\ & \kern-1em h = r \, v_\perp \quad\quad \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\maru{2} \end{array} \right . \] 上記2式を若干面倒な式変形と積分をしていくと,星Bの星Aからの距離 $r$ を,動径ベクトルが $x$ 軸となす角 $\theta$ の関数として表していくことができます(式変形の詳細は こちら )。ここで $x$ 軸は,星Bが星Aに最も近づく位置(距離 $r$ が最小となる位置。近点)と星Aを結ぶ方向とし,角 $\theta$ は $x$ 軸から反時計回りにはかった角度とします。(星Aが太陽である場合の近点は『近日点』,星Aが地球である場合なら『近地点』と呼ばれる。)
その関係式は,次式のようになります。\[r = \bun{\bun{h^2}{G M}}{1 - \kon{1 + \bun{2E h^2 }{G^2 M^2 m}}\cdot \cos\theta} \quad\quad \cdots\cdots\maru{3}\] よって,\[\color{red}{ r_0 = \bun{h^2}{G M} }\quad \cdots\cdots\cdots\cdots \maru{4} \\ \color{red}{e = \kon{1 + \bun{2E h^2 }{G^2 M^2 m}} } \quad \cdots\cdots \maru{5} \]とおくと,上式は,\[\color{red}{r = \bun{r_0} { 1 - e \,\cos\theta } } \quad\quad \cdots\cdots\cdots \maru{6}\]となります。 $r_0$ は距離の次元を持つ量であり, $e$ は離心率と呼ばれている物理量です。この $\maru{6}$ 式が,万有引力を受けた物体の運動軌跡に関する基本式です。
次に $\maru{6}$ 式を, $x-y$ 座標系に書き直していきます。$\maru{6}$ 式を以下のように式変形します。\[r (1 - e \cos\theta) = r_0 \\ \kern-1em \therefore r = r_0 + r\, e \cos\theta \\ \kern-1em \therefore r^2 = r_0{}^2 + 2 e r_0 \,(r \cos\theta) + e^2 (r \cos\theta)^2 \] ここで星Bの位置を $x-y$ 座標系で表せば,\[x = r \,\cos\theta \\ y = r \,\sin\theta \\ \kern-1em \therefore r^2 = ( r \,\cos\theta )^2 + ( r \,\sin\theta )^2 = x^2 + y^2 \]ですから,これを前式に代入すると,\[x^2 + y^2 = r_0{}^2 + 2 e \,r_0\, x + e^2\, x^2 \\ \kern-1em \therefore (1 - e^2)x^2 -2e\,r_0 x + y^2 =r_0{}^2 \quad \cdots\cdots\maru{7}\]となり,星Bの運動軌跡は2次曲線になることが分かります。
一般に,万有引力やクーロン力など距離の2乗の反比例する力を受けた物体の運動軌跡は2次曲線になります。
◎力学的エネルギーと軌道の形:
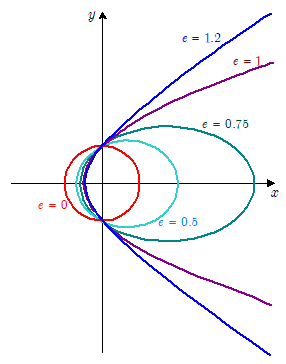
$\maru{7}$ 式で表される2次曲線がどのような形の曲線になるかは,離心率 $e$ ,したがって $\maru{5}$ 式より,力学的エネルギー $E$ の値に左右されます。
(i) $E \lt 0$ ならば,楕円軌道
$E \lt 0$ の場合, $\maru{5}$ 式より, $e \lt 1$
よって $\maru{7}$ 式より,\[x^2 - \bun{2e \,r_0}{1 - e^2}x + \bun{y^2}{1 - e^2} = \bun{r_0{}^2}{1 - e^2} \\ \kern-1em \therefore \bigg( x - \bun{e}{1 -e^2}r_0 \bigg)^2 + \bun{y^2}{1 - e^2} = \bun{r_0{}^2}{1 - e^2} + \bun{e^2 \, r_0{}^2}{(1 - e^2)^2} \\ \kern-1em \therefore \bigg( x - \bun{e}{1 -e^2}r_0 \bigg)^2 + \bun{y^2}{1 - e^2} = \bun{r_0{}^2}{(1 - e^2)^2} \\ \kern-1em \therefore \bigg[\bun{ x - e r_0/(1 - e^2)}{r_0/(1 - e^2)}\bigg]^2 + \bigg[\bun{y}{ r_0/\kon{1 - e^2}}\bigg]^2 = 1 \] よって,\[a = \bun{r_0}{1 - e^2} \\ b = \bun{r_0}{\kon{1 - e^2}} \]とおけば,\[ \bigg( \bun{x -e\, a }{a}\bigg)^2 + \bigg(\bun{y}{b}\bigg)^2 = 1 \]となり, $a$ を長半径, $b$ を短半径とする楕円であることが分かります。
すなわち, $E \lt 0$ ならば,星Bは星Aの引力からは逃れられず,星Aの周りで楕円運動をすることになります。
$e = 0$ ならば,軌道は「円」になります。
(ii) $E = 0$ ならば,放物線軌道
$E = 0$ の場合, $\maru{5}$ 式より, $e =1 $
$\maru{7}$ 式より,\[ -2r_0\,x + y^2 = r_0{}^2 \\ \kern-1em \therefore x + \bun{r_0}{2} = \bun{1}{2r_0}y^2 \] この曲線は,放物線です。
よって, $E = 0$ の場合,星Bは放物線を描いて無限遠に飛び去ることになり,星Aの引力圏から脱出してしまいます。
(iii) $E \gt 0$ ならば,双曲線軌道
$E \gt 0$ の場合, $\maru{5}$ 式より, $e \gt 1 $
$\maru{7}$ 式において $e \gt 1$ を考慮して ,\[x^2 + \bun{2e \,r_0}{ e^2 - 1}x - \bun{y^2}{ e^2 - 1} = -\bun{r_0{}^2}{ e^2 - 1} \\ \kern-1em \therefore \bigg( x + \bun{e}{e^2 - 1}r_0 \bigg)^2 - \bun{y^2}{ e^2 - 1} = -\bun{r_0{}^2}{ e^2 - 1} + \bun{e^2\,r_0{}^2}{( e^2 - 1)^2} \\ \kern-1em \therefore \bigg( x + \bun{e}{e^2 - 1}r_0 \bigg)^2 - \bun{y^2}{ e^2 - 1} = \bun{r_0{}^2}{( e^2 - 1)^2} \\ \kern-1em \therefore \bigg[\bun{ x + e r_0/( e^2 - 1)}{r_0/( e^2 - 1)}\bigg]^2 - \bigg[\bun{y}{ r_0/\kon{ e^2 - 1}}\bigg]^2 = 1 \] よって,\[a = \bun{r_0}{ e^2 - 1} \\ b = \bun{r_0}{\kon{ e^2 - 1}} \]とおけば,\[ \bigg( \bun{x + e\, a }{a}\bigg)^2 - \bigg(\bun{y}{b}\bigg)^2 = 1 \]となり, 双曲線になります。
よって, $E \gt 0$ の場合,星Bは双曲線を描いて無限遠に飛び去ることになり,星Aの引力圏から脱出していきます。
次のテーマ『引力圏脱出のための効果的ガス噴射』に続く。