☆概　要：
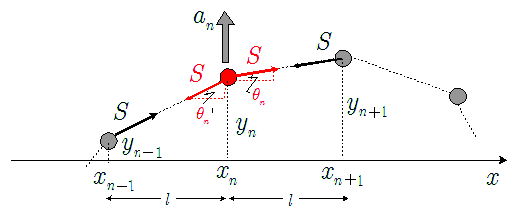
　上図のように質点が並んでいるとき，$(n-1)$番目，$n$番目，$(n+1)$番目の各粒子の変位がそれぞれ$y_{n-1}$，$y_n$，$y_{n+1}$であるとき，$n$番目粒子の質量を$m$，加速度を$a_n$，各粒子間にはたらく力を$S$とすると，$n$番目粒子の運動方程式は，\[ 　ma_n=S\times\sin\theta_n-S\times\sin\theta_n{}' \\　　\kinji S\times\tan\theta_n-S\times\tan\theta_n{}' \\　　\kinji S\bun{y_{n+1}-y_n}{l}-S\bun{y_n-y_{n-1}}{l} \\ 　　=-\bun{S}{l}(2y_n-y_{n+1}-y_{n-1}) \cdots\cdots\maru{1}\]となる。これらの運動方程式を媒質粒子の数だけ立てて，その連立方程式をルンゲ・クッタ法と呼ばれる解析法で数値解析しているのが本シミュレーションである。
　このシミュレーションは，きわめて単純化したモデルではあるが，媒質各粒子の振る舞いを力学面から解析したものであり，実際の波動の発生に近い状況を表していると考えられる。
　ただしこのモデルでは，媒質両端における無反射条件が考慮されていない。先の理論式によるシミュレーションの場合，無限に続く媒質上における理論式を元にしたシミュレーションであり，媒質境界における反射は一切ないものとしている。現実には無限に続く媒質はこの世には存在しないわけで，有限である。有限であれば必ず媒質の『端』があり，現実には境界からの反射の影響が必ずあることになる。その意味では，むしろ本シミュレーションの方が実態に近いともいえる。

☆詳　解：
　
　上記の質点列に振動が入射してきたとして，このときこの振動がこの質点列を伝わっていく速さ$v$を求めてみよう。さらにこのことから，連続的な媒質，たとえば弦などを伝わる波の速さを推測してみよう。

　入射した振動により，各質点は周期$T$の単振動をするものとする。このとき$n$番目，$(n-1)$番目，$(n+1)$番目の各粒子の時刻$t$での変位$y_n$，$y_{n-1}$，$y_{n+1}$がそれぞれ以下のように表させるものとする。 　\[ \left \{ \begin{array}{rl} & \kern -1em y_n=a\sin\bigg(\bun{2\pi}{T}t+\delta\bigg)\\ & \kern -1em y_{n-1}=a\sin\bigg\{\bun{2\pi}{T}\bigg(t+\bun{l}{v}\bigg)+\delta\bigg\} \\ & \kern -1em y_{n+1}=a\sin\bigg\{\bun{2\pi}{T}\bigg(t-\bun{l}{v}\bigg)+\delta\bigg\} \end{array} \right . \] 　ここで，$l\,$は粒子間の間隔，$\delta$は初期位相である。振動が$n$の小さい方から伝わってきているとすると，$(n-1)$番目の粒子は$n$番目の粒子より$\bun{l}{v}$の時間だけ早く振動が伝わっており，振動がその分だけ先行していることになる。逆に$(n+1)$番目の粒子は$n$番目の粒子より$\bun{l}{v}$の時間だけ遅れて振動しているので，上式のように表されることになる。
　ここで， \[　y_{n-1}+y_{n+1}=a\sin\bigg\{\bun{2\pi}{T}\bigg(t+\bun{l}{v}\bigg)+\delta\bigg\}+a\sin\bigg\{\bun{2\pi}{T}\bigg(t-\bun{l}{v}\bigg)+\delta\bigg\} \\ 　　　　　=2a\cos\bigg(\bun{2\pi l}{Tv}\bigg)\times \sin\bigg(\bun{2\pi}{T}t+\delta\bigg)\\ 　　　　　=2\cos\bigg(\bun{2\pi l}{Tv}\bigg)\times y_n\cdots\cdots\maru{2} \] であるから，$n$番目粒子の運動方程式は，前記$\maru{1}$式に$y_n$，$y_{n-1}$，$y_{n+1}$を代入して，\[　ma_n=-\bun{S}{l}(2y_n - y_{n-1} - y_{n+1})\\　=-\bun{2S}{l}\bigg\{1-\cos\bigg(\bun{2\pi l}{Tv}\bigg)\bigg\}\times y_n \cdots\cdots\maru{3} \] 　これが$n$番目粒子の運動方程式であり，確かに単振動の運動方程式の形になっている。
　一方各粒子は周期$T$の単振動をしているのであるから，その運動方程式は一般式として，角振動数を$\omega=\bun{2\pi}{T}$として，\[　a_n=-\omega^2\cdot y_n=-\bigg(\bun{2\pi}{T}\bigg)^2\cdot y_n \cdots\cdots\maru{4}\]と表されるはずである。$\maru{3}$と$\maru{4}$の比較より，
　（$ \cos\theta=1-2\sin^2\bun{\theta}{2}$　の公式を利用）\[　\bigg(\bun{2\pi}{T}\bigg)^2=\bun{2S}{ml}\bigg\{1-\cos\bigg(\bun{2\pi l}{Tv}\bigg)\bigg\}\\ 　　　=\bun{2S}{ml}\bigg[1-\bigg\{ 1-2\sin^2\bigg( \bun{2\pi l}{2Tv} \bigg) \bigg\} \bigg]\\　　　= \bun{4S}{ml}\sin^2\bigg(\bun{\pi l}{Tv}\bigg) \\ \therefore \bun{2\pi}{T}=2\kon{\bun{S}{ml}\,}\,\sin\bigg(\bun{\pi l}{Tv}\bigg)\] 　ここで$v$は振動が伝わっていく速さであり，これに周期$T$を乗じた値$Tv$は，波動で言うならば１波長$\lambda$に相当する。よって質点が十分に密に詰まっているとして　$l \ll \lambda=Tv$　であるならば，$\bigg(\bun{\pi l}{Tv}\bigg) \ll 1$　が言える。よって$\theta \ll 1$のとき成り立つ　$\sin\theta \kinji \theta$　なる近似式を適用して，\[　\bun{2\pi}{T}=2\kon{\bun{S}{ml}\,}\,\sin\bigg(\bun{\pi l}{Tv}\bigg) \kinji 2\kon{\bun{S}{ml}\,}\,\times \bun{\pi l}{Tv} \\　\therefore v=\kon{\bun{Sl}{m}}=\kon{\bun{S}{m/l}}\] 　これが，この場合の質点列を振動が伝わっていく速さとなる。
　ここで$\bun{m}{l}$は，質点間隔 $l$ 中に含まれている質点の質量ですが，質点の間隔をどんどん詰めて $l$ の値を小さくしていったと考えると，$\bun{m}{l}$ は弦のような連続体の場合の線密度に相当する量になります。よって$S$を弦の張力に相当すると考えると，よく知られた弦を伝わる横波の速さと同じ式になります。\[ 　弦を伝わる横波の速さ v=\kon{\bun{S}{\rho}}\quad (\rho:線密度，S:弦の張力) \]