図１のように，２スリットに光を照射すると，後方のフィルムまたはスクリーンに干渉縞ができる。光を波動と考えれば，Ｓ₁，Ｓ₂を通った２つの波の合成として，干渉縞ができることは容易に分かる。

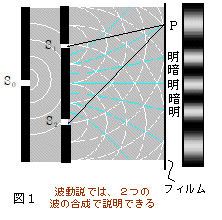
　これに対して光を粒子－光子－と考えると，話はかなり混乱してくる。粒子であれば，スリットＳ₁かＳ₂のいずれかを通ってフィルム上の１点に届く・・・というのが最も普通の考え方である(図２参照）。

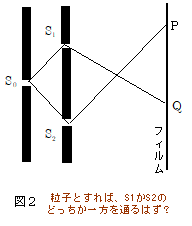
　上の考えが正しいかどうかは，Ｓ₁，Ｓ₂の一方をふさいでそれぞれスリットがどちらか一方のみしか開いていない状態にして実験をし，それぞれの実験による光の強度分布を重ねたものと，２つのスリットが両方とも開いているときの光強度分布が一致するかどうかを調べればよいことになろう。

　しかしこの期待は見事に外れ，それぞれのスリットを１つずつ開いたときの分布を重ねても，２つのスリットを同時に開いたときの分布にはならなかった。つまりスリットが１つずつと２つ同時とでは，フィルムに記録される縞模様の様子は一変するのである。

　スリットが２つあってはじめて干渉縞ができるということは，１つの光子が同時に２つのスリットを通って干渉したと考えるべきなのだろうか・・・？　あるいは粒子だから異なる場所を同時に通過するなんてできない・・・と考えるならば，一方のスリットを光子が通過する際に通ってもいない他方のスリットの影響を受けたと考えるべきなのだろうか・・・？　また仮にそうだとしたら，そのメカニズムは・・・？

　このように，光の二重性の問題は，これまでの我々の常識を覆す重大な内容を含んでいたのである。

　同様の実験は，２スリットに電子線を照射することでも確認できた。つまり粒子と考えられていた電子も波動として振舞い，干渉縞をつくったのである。ここで注目したい点は，この場合実験装置内に常に電子が１個しか存在しない程度に十分に低い密度で実験を行なったにもかかわらず，フィルムには干渉縞が記録されたということである。つまり，２個の電子が相互作用したわけではなく，ポツンポツンと１個ずつ電子を入射させても，時間の経過とともに入射電子数の合計が多くなるにつれて干渉縞が現れてくるのである。

　ともかくはっきりしていることは，２つのスリットの存在が光子や電子の振る舞いを決定付けていること。そして我々が確認できることは，最終的には光子や電子の届く 『個数』 が場所によって異なり，その結果届く数が多ければ明線，少なければ暗線といった具合に縞模様ができるという事実である。　

　このようなことから，現在，二重性については，おおよそ次のように解釈されている。

　光子や電子は，フィルムやスクリーン（または検出器）にぶつかるまでは空間を伝播する波動として扱うことができ，したがって個々の光子・電子の位置を確定することはできない。これらが他の物体にぶつかった瞬間に波動性は消失し，粒子として振舞いその位置が確定する。その存在頻度（存在確率）は２つの波の合成，つまり干渉として求めることができる・・・という考え方である。平たく言えば，個々の光子・電子は勝手な方向に飛んでいくが，全体としては干渉で強め合う位置には沢山の光子・電子が届くヨ・・・ということである。このような考え方を「確率解釈」という。（実際にはシュレーディンガー方程式という方程式を満たす波動関数というもので存在確率密度が計算される。）

　このような考え方に基づいて，多数の光子の集団によって干渉縞ができていく様子をシミュレートしたのが先のシミュレーションである。光子数が少ない内は各光子は一見バラバラに分布していくように見える。しかし全体として入射個数が多くなるに従い，多くの光子が届く位置とそうでない位置が次第にはっきりしてくる。

　実際の写真を撮る場合も，シャッター時間が極めて短いと入射する光子数も少なく，したがってフィルム上のバラバラの位置が感光していて何が写っているのか分からない写真になる。しかしシャッター時間が長くなるにつれて入射光子数も多くなり，写るべく姿がフィルムに記録されるようになり，被写体の像が浮かび上がってくる。逆に露出時間が長くなり過ぎると本来確率の小さいところにも光子が届いてしまい，フィルム全体が感光することになる。

　　　戻る