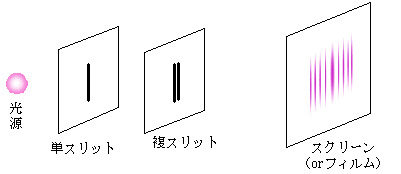
本シュミレーションでは,下図のような2スリット(複スリット)型干渉計に光を照射したとき光子が分布していく様を,光の強度分布に比例した出現頻度で乱数を発生・プロットすることにより模擬的にシミュレートしています。2スリットに電子を照射したときにも、同様の現象が見られることが知られています。
◎操作方法:
「スタート」ボタンを押してください。小さな点が次々とプロットされていきますが,しばらくすると,縞模様らしきものが現れてきます。光の「粒子性」を模したシミュレーションです。
グラフの横軸は,
2スリット間の光路差「⊿=dsinθ」を表します。ここで「
d」は,
2つのスリット間の間隔を表します。またそのスリット自身の幅を「
a」で表し,「スリット幅
a」および「波長 λ」は「スリット間隔
d」の何倍かで表しています。
詳細は,
干渉・回折を参照してください。
☆概 要:
光は波動性と粒子性をあわせ持ちます。回折,干渉といった現象は光の波動性で説明されますが,光電効果やコンプトン効果などは光を粒子と考えないと説明がつきません。このような波動性と粒子性は「
二重性の問題」といって,その物理的解釈をめぐって,20世紀はじめに物理学者を大いに悩ませました。
たとえば光を2スリットに通せば,後ろに置かれたフィルムには干渉縞が記録されます。干渉縞ができるのは光の波動性で説明できますが,フィルムの銀塩粒子1個1個を感光させるという面ではむしろ光を粒子と考えた方が説得力があります。
上のシミュレーションは,2スリットに多数の光子を入射させたと考えたときの光子の到達点を模擬的にシミュレートしたものです。個々の光子はランダムに飛んでいき,フィルム上のどこかに届きますが,どこに届くかは全く予測できません。しかし入射光子数が多くなるにつれて,ぼんやりと干渉縞らしきものが浮かび上がってきます。
理由は簡単です。明線位置には多くの光子が届き,暗線位置には光子はほとんど届いていないということです。どうやら波動説で説明される「光波の干渉」というのは,光子の届きやすさ・届きにくさと関係ありそうです。
グラフは,2スリットに光を照射したときに見られる光の強度分布を,波動の式を使って求め,それをグラフにしたものです。赤線は回折の効果を表す曲線,緑線が干渉を含めた全体の光の強度を表します。
本シミュレーションは,この光の強度分布に比例した出現頻度で乱数を発生させ,これをプロットしたものです。
光の二重性

