つぎに,$f(\theta)$ について考える。
$f(\theta)$ は,回折角 $\theta$ の方向に回折した光波の振幅に関わる量であるから,各スリットを通ったときの回折そのものについて考えていく必要がある。
先の議論ではスリットの幅については全く触れてなかったが,もちろんスリットにも幅がある。このスリットのごく狭く開いた部分を波が通るときに回折が起きるわけであるが,このとき回折する角度 $\theta$ によって回折光の強さそのものに違いが出てくる・・・・というわけである。
下図は,スリット部分を拡大したものである。
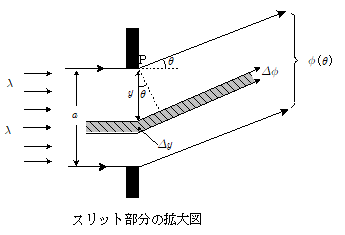
スリットの幅は $a$ とする。
まず,回折角 $\theta=0$,すなわち回折することなく直進する光波 $\phi(0)$ の振幅を $A(0)$ とする。 $A(0)$ は, $\theta=0$ 方向に進む光波のスリット幅 $a$ 全体としての合成波の振幅であるから,スリットの単位幅当たりに含まれる光線束の光波の振幅は $\bun{A(0)}{a}$ と考えてよいだろう。よって上図において,スリットの上端部を通った光波を $\bun{A(0)}{a}\sin2\pi\nu t$ とすると,上端から距離 $y$ の位置にある微小幅 $\varDelta y$ を通った光線束が角 $\theta$ の方向に回折した場合,その光波 $\varDelta \phi(\theta)$ は,上端を通った光との間に $y\sin\theta$ の光路差があることを考慮して,\[\varDelta \phi(\theta)=\bun{A(0)}{a}\cdot \sin2\pi\bigg(\nu t-\bun{y \sin\theta}{\lambda}\bigg) \times \varDelta y \]と表すことができる。ただし $\varDelta y$ は極めて微小であり,この範囲内での光波の位相差は無視できるとする。
よって,スリット幅 $a$ 全体を通って角 $\theta$ 方向に進む回折光 $\phi(\theta)$ は, スリット幅 全体についての$\varDelta \phi(\theta)$の和(合計)ということになり,したがって $\varDelta \phi(\theta)$ のスリット幅 $a$ における積分を考えればよいことになる。 \[\kern-1em \phi(\theta)=\int^{a} _{0} d\phi (\theta) \\ \quad = \bun{A(0)}{a}\int^{a} _{0} \sin2\pi\bigg(\nu t-\bun{y \sin\theta}{\lambda}\bigg)dy \\ \quad =\bun{A(0)}{a}\cdot \bun{\lambda}{2\pi\sin\theta} \bigg[\cos2\pi\bigg(\nu t-\bun{y \, \sin\theta}{\lambda}\bigg) \bigg]_0^a \\ \quad =\bun{A(0)}{a}\cdot \bun{\lambda}{2\pi\sin\theta} \bigg[\cos2\pi\bigg(\nu t-\bun{a\sin\theta}{\lambda}\bigg)-\cos2\pi\nu t \bigg] \] ここで $\cos\alpha-\cos\beta = -2\sin\bun{\alpha-\beta}{2} \cdot \sin\bun{\alpha+\beta}{2}$ の公式を利用すると,上式は,\[ \kern-1em \phi(\theta) = \bun{ A(0)\cdot \lambda}{2\pi a \sin\theta} \times 2\sin\bigg(\bun{\backslash \kern-0.5em 2\pi}{\backslash \kern-0.5em 2\lambda }a\sin\theta\bigg) \cdot \sin2\pi\bigg( \nu t-\bun{a\sin\theta}{2\lambda}\bigg) \\ \quad =\bun{\sin\bigg(\bun{\pi a \sin\theta}{\lambda}\bigg)}{\bun{\pi a \sin\theta}{\lambda}}\cdot A(0) \times \sin2\pi\bigg( \nu t-\bun{a\sin\theta}{2\lambda}\bigg) \]よって,回折角 $\theta$ 方向の回折光 $\phi(\theta)$ の振幅 $A(\theta)$ は,上式右辺第1項の絶対値として与えられ,\[A(\theta)=\bigg|\bun{\sin\bigg(\bun{\pi a \sin\theta}{\lambda}\bigg)}{\bun{\pi \sin\theta}{\lambda}}\bigg|\times A(0) \]である。したがって,\[\therefore \bun{A(\theta)}{A(0)}= \bigg|\bun{\sin\bigg(\bun{\pi a \sin\theta}{\lambda}\bigg)}{\bun{\pi a \sin\theta}{\lambda}}\bigg| \\ \therefore f(\theta)=\bigg \{ \bun{A(\theta)}{A(0)}\bigg \}^2= \bigg[\bun{\sin\bigg(\bun{\pi a \sin\theta}{\lambda}\bigg)}{\bun{\pi a \sin\theta}{\lambda}}\bigg]^2 \cdots\cdots\maru{5}\] これが $\maru{1}$ 式で仮定した $f(\theta)$ の中身である。ここで $a\sin\theta$ は,スリットの上端を通った光とスリットの下端を通った光との光路差に相当する。
$\bigg(\bun{\sin x}{x}\bigg)^2$ のグラフを参考にして $f(\theta)$ と $a\sin\theta$ の関係をグラフにすると,およそ下図のようになる(下の<参考>を参照)。

\[\kern-1em \varDelta _{回折}=a\sin\theta= \left \{ \begin{array}{rl} & \kern-1em 0 → f(\theta)=max → 強度最大 \\ & \kern-1em m\lambda → f(\theta)=0 → 強度は0\\ & \kern-1em (m=\:\pm1,\:\pm2,\:\pm3,\:\cdots\:,|m| < a/\lambda,0 を含まず。) \end{array} \right . \quad\cdots\cdots\maru{6} \]
という関係があることがわかる。この関係は,先に述べた干渉条件$\maru{4}$とは逆のような関係になっていることに注意しよう。なお上述の関数 $f(\theta)$ は, $a\sin\theta = \pm 1.5\lambda$ , $\pm 2.5\lambda$ , $\cdots$ の付近 ( 厳密には少し手前)で極大値を持つが,その値は約 $0.047\cdots$ , $0.016\cdots$ , $\cdots$ と, 回折角$\theta$ の増大とともに急速に小さくなっていく。
<参考> $y=\bigg(\bun{\sin\,x}{x}\bigg)^2$ とすると,関数 $y$ の極大値,極小値は $y$ の微係数を $0$ とおいて,\[\kern2em y'=\bun{2\sin\,x\:\cdot\:( x \cdot\cos\,x - \sin\, x)}{x^3} \\ \quad\quad\quad =\bun{2\sin\,x}{x}\cdot \bun{x\cdot\cos\,x - \sin\, x}{x^2} = 0 \\ \kern1em \therefore \left \{ \begin{array}{rl} & \kern-1em x=0 で y=1 \quad ( 最大値 )\\ & \kern-1em x=m\,\pi (\:m=\pm1,\:\pm2,\:\cdots\:) で y=0\quad(最小値) \\ & \kern-1em x=\tan\,x を満たす\,x \,で y=極大値 \\ & \kern-1em ( x=\pm1.430\pi,\:\pm2.459\pi,\: \pm3.470\pi,\cdots など) \end{array} \right . \]となる。
上記 $\maru{6}$ の関係式から分かるように,最初に $f(\theta)=0$ ,すなわち光の強度が最初に $0$ となるのは,\[a\sin\theta=\lambda \quad \therefore \sin\theta=\bun{\lambda}{a}\]を満たす角 $\theta$ の方向である。これより $\lambda$ が大きいほど,また $a$ が小さいほど光強度が最初に $0$ になる角度は大きいわけで,波長の長い波ほど,またスリット幅が小さいほど回折が大きく起こりやすいことを意味する。つまり,長波長の波は回折によって広がりやすく,短波長の波は広がりにくく直進性が大きい…と言える。山奥でラジオは受信できてもテレビの受信がしにくいのは,ラジオの電波(中波:波長数百m)よりもテレビの電波(UHF:波長数十cm)の方が波長が短く,回折が起きにくく,山の裏に回り込みにくいからである。
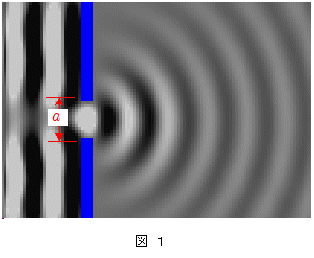
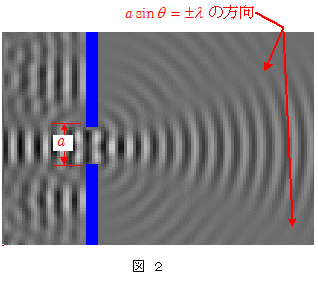
下の図1,図2は,同じスリット幅 $a$ のスリットに対して,図1は $a \kinji \lambda$ の波が,図2は $a \kinji 2\lambda$ の波が入射した場合の回折の様子を示す。図1の場合は回折角 $\theta$ が $90^\circ$ に近い障壁の裏側奥深くまで強い波が回り込んでいるのに対し,図2の場合は強い波の伝わる回折角はかなり狭まっており, $\theta \approx \pm30^\circ $ $(\: a\sin\theta=\pm\lambda $ において,$ a \approx 2\lambda\quad\therefore \theta \approx \pm30^\circ \:)$ の方向では $f(\theta)=0$ となって波が消えているのが確認できる。
なお下の2つの図は,本ホームぺページの「波のシミュレーション」で作成したものです。参考にしてください(Java Aplletで動作)。
戻る(干渉による効果) 次へ(全体としての光強度)