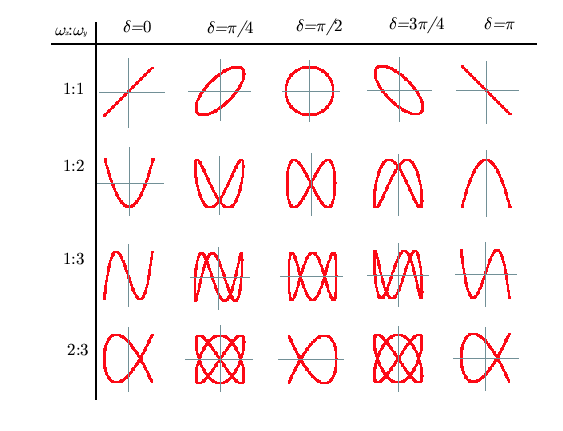
上図のリサジュー図形において,$x$ 方向,$y$ 方向の変位$x$ ,$y$ が時間 $t$ の関数として,次式で与えられるとします。 \[x = A_x \cdot \cos \omega_x \, t \\ y = A_y \cdot \cos ( \omega_y \, t + \delta ) \]
上図の1段目は $\omega_x = \omega_y$ のケースですが,この場合に描かれる図形は一般に楕円(円を含む)であり,さらに $\delta = 0$ または $\delta = \pm \pi$ であれば楕円が完全につぶれた形としての「直線」となります。
以下, $\omega_x = \omega_y$ の場合に描かれるリサジュー図形について,数式を用いて確認してみましょう。
入試対策上必要と思われるのも,以下の1.~3. の3ケースに限られます。
1. $\omega_x = \omega_y = \omega$ で, $\delta = 0$ の場合:
\[x = A_x \cdot \cos \omega \, t \\ y = A_y \cdot \cos \omega \, t \\ \kern-1em \therefore \bun{ \, y \,}{x} = \bun{\, A_y \,}{A_x} \quad\cdots \cdots \color{red}{直線} \]
2. $\omega_x = \omega_y = \omega$ で, $\delta = \pm \pi$ の場合:
\[x = A_x \cdot \cos \omega \, t \\ y = A_y \cdot \cos (\, \omega \, t \pm \pi\,) = -A_y\cdot \cos \omega \, t \\ \kern-1em \therefore \bun{ \, y \,}{x} = - \bun{\, A_y \,}{A_x} \quad\cdots \cdots \color{red}{直線} \]
3. $\omega_x = \omega_y = \omega$ で, $\delta = \pm \bun{\pi}{2}$ の場合:
\[x = A_x \cdot \cos \omega \, t \\ y = A_y \cdot \cos (\, \omega \, t \pm \bun{\pi}{2}\,) = \mp A_y\cdot \sin \omega \, t \\ \kern-1em \therefore \bigg(\bun{x}{A_x} \bigg)^2 + \bigg(\bun{y}{A_y} \bigg)^2= 1 \quad\cdots \cdots \color{red}{楕円} \\ \kern1em A_x = A_y \quad なら\cdots \cdots \color{red}{円} \]
4. $\omega_x = \omega_y = \omega$ で, $\delta $ が任意の値の場合:
\[x = A_x \cdot \cos \omega \, t \\ \kern 1em \therefore \bun{x}{\, A_x\,} = \cos \omega \, t \quad\cdots\cdots \maru{1} \\ y = A_y \cdot \cos (\, \omega \, t + \delta\,) \\ \kern1em = A_y \cdot (\, \cos \, \omega \, t \cdot \cos\,\delta - \sin \, \omega \, t \cdot \sin\,\delta \,) \quad\cdots\cdots\maru{2} \] $\maru{1}$ 式,$\maru{2}$ 式より, \[\bun{y}{\,A_y\,} = \cos \, \omega \, t \cdot \cos\,\delta - \sin \, \omega \, t \cdot \sin\,\delta \\ \kern2em = \bun{x}{\,A_x \,}\cdot \cos \delta - \sin \,\omega \, t \cdot \sin\delta \\ \kern-1em \therefore \bun{y}{\,A_y\,} - \bun{x}{\,A_x \,}\cdot \cos \delta = - \sin \,\omega \, t \cdot \sin\delta \quad\cdots\cdots\maru{3}\] $\maru{1}^2 \times \sin^2\delta$ より,\[\bigg(\bun{x}{\,A_x \,}\bigg)^2 \times \sin^2\delta = \cos^2\omega \, t \times \sin^2\delta \quad\cdots\cdots\maru{1}'\] $\maru{3}^2 $ より,\[\kern-2em \bigg(\bun{y}{A_y }\bigg)^2 - 2\times \bun{y}{A_y }\times \bun{x}{A_x }\cdot \cos \,\delta + \bigg(\bun{x}{\,A_x \,}\bigg)^2\cdot \cos^2 \delta \\ \kern11em = \sin^2 \omega\,t \cdot \sin^2 \,\delta \quad\cdots\cdots\maru{3}'\] $\maru{1}' + \maru{3}'$ より,\[\bigg(\bun{x}{\,A_x \,}\bigg)^2 + \bigg(\bun{y}{A_y }\bigg)^2 - 2 \bun{x}{A_x } \bun{y}{A_y }\cdot \cos \,\delta = \sin^2\,\delta \quad\cdots\cdots\maru{4} \] $\maru{4}$ 式は, $x = \pm A_x$ , $y = \pm A_y$ の矩形に内接する楕円を表します。
【参考】 $\maru{4}$ 式は,座標軸を反時計回りを正として,\[\tan 2\theta = \bun{2 A_x \, A_y }{A_x{}^2 - A_y{}^2}\cdot \cos \delta \]を満たす角 $\theta$ だけ回転した楕円となります。ただし, $A_x = A_y$ の場合は, $\cos \delta $ が正ならば $\theta = 45^\circ $ ,負ならば $\theta = -45^\circ $ となります。