直角な2方向の単振動を組み合わせたときに描かれる図形をリサジュー図形といいます。フランスのリサジューという物理学者が自ら考案した装置で様々な図形を得て,研究したというのでこの名があります。
角振動数比や位相差をいろいろ変えてみて下さい。面白い図形が見られるかもしれません。
「角振動数」,「振幅」,「位相差」の値は,それぞれスライダー,もしくは「特定値の選択」から選んで変更できます。
変更後の新しい値を反映させるために,念のため「リセット」ボタンを押してから「スタート」させてください。
◎概 要:
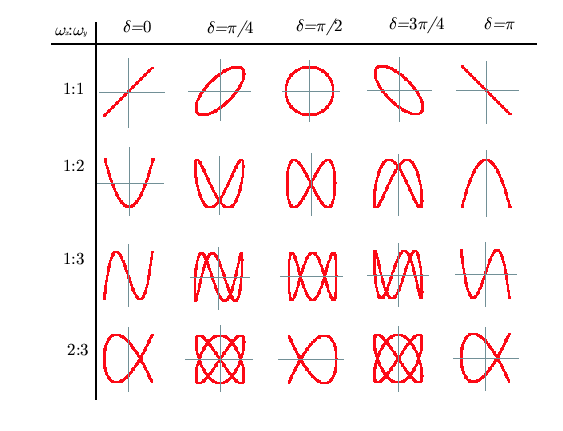
下に,いくつかのリサージュ図形を示します。 δ は, x 軸方向の振動に対する y 軸方向の振動の位相差を表します。
下表の1段目に示したように,円も楕円も同周期の直角な2方向の単振動の組み合わせとみなすことができることが分かります。
数式を使った解説は「解説-1」を参照ください。
◎図形の繰り返しは,振動数の比が鍵:
振動数(角振動数)比,または周期比が既約分数の形に表せるとき,すなわち 有理数 であるとき,軌跡はある時間の経過後に必ず,以前に描いた図形上を再び辿り,以後繰り返し同じ図形を描き続けます。繰り返しになるまでの振動回数は,既約分数の分子・分母の数値で決まります。
例えば角振動数比 ωy / ωx = 1.2 の場合,
ωy / ωx = 1.2 = 6 / 5
ですので,y方向に6回,x方向に5回振動した時点から,同じ図形の繰り返し描画が始まります。(周期比で表せば,Ty / Tx = 1 / 1.2 = 5 / 6 となる。)
これに対して振動数比や周期比が既約分数の形に表せない,つまり 無理数 の場合,時間がたっても以前と同じ軌跡を描くことはなく,常に異なるルートを通ります。したがって時間経過とともに,矩形で囲まれた部分が新しいルートで覆い尽されていく(塗り潰される)ことになります。つまり,リサジュー図形は形成されせん。上のシミュレーションにおいて,角振動数比「特定値の選択」欄内にある*印 √2 および π(パイ)の場合がこれに該当します。試してみてください。
詳しくは,「解説-2 」 を参照ください。