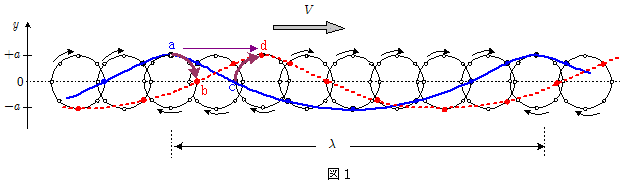
上図は,この様子を模式的に示したものである。それぞれ水は,すべて同じ周期,同じ半径の等速円運動をしており,水の円運動は波の進行方向側(上図の右方)ほど位相が進んでいる(回転角が大きくなっている)。
はじめ青線で示したような波形になっていたとしよう。その $1/4$ 周期後にはそれぞれ水が円運動を $90^\circ$ ずつ回転し(上図の場合,時計回りに回転),たとえば上図のa点の位置にあった水は $1/4$ 回転後b点の位置に,c点にあった水はd点の位置にくる。このような回転運動をすべての水がおこなうと,水の $1/4$ 回転によって,あたかも波が $1/4$ 波長分進んだような形になる(赤い破線で示した波)。このように,水がそれぞれ円運動を続けることによって,波が進んでいくように見えることになる。
水が円運動を起こすのに働く力が重力である場合重力波といい,水の表面張力である場合表面張力波という。
以下では,重力波について,その伝わる速さを求めてみよう。
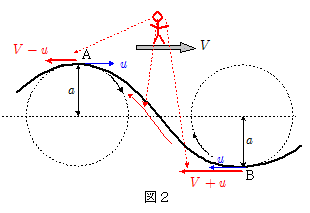
上図のように,水はそれぞれ半径 $a$ ,周期 $T$ の等速円運動をしているとし,波の波長を $\lambda$ ,波の伝わる速さを $V$ とする。このとき水の円運動の速さ $u$ は,円運動の速さと角速度の関係より, \[u=半径 a \times 角速度 \omega \] ここで角速度 $\omega$ は $ \omega = \bun{2\pi}{T} $であるから,\[u= a \times \omega = a\times \bun{2\pi}{T} \]である。
いま,波の速さ $V$ で運動する観測者(赤色で示した)を想定すると,この観測者に対する波の相対的な移動速度はゼロ,したがってこの観測者に対して波は形を変えることなくこの観測者に対して静止して見えるはずである。ただし水は動いているので,この観測者から見ると,あたかもこの観測者の足元に静止している波形に沿って定常的な水の流れがあるように見えることになるだろう。このときの観測者に対する水の流れの速さは,波の山A,谷Bでそれぞれ\[山A: V -u = V - \bun{2\pi}{T} a \\ 谷B: V + u = V + \bun{2\pi}{T} a\] である。ここでこの観測者は等速度で運動しているのであるから慣性系であり,したがってこの観測者から見て,水面の流線に沿って流れる水の流れについて力学的エネルギー保存が成り立つ。よって水の密度を $\rho$ とすれば,単位体積あたりの水について,山Aと谷Bに関して以下の関係式が成り立つ。( $g$ は重力加速度。) \[\bun{1}{2}\rho (V-u)^2 + \rho g (a+a) = \bun{1}{2}\rho (V+u)^2 \\ \therefore g a = u V \\ \therefore g a = \bun{2\pi}{T}a V \\ \therefore V = \bun{g T}{2\pi} \cdots\cdots\maru{1} \] 一方,波の波長,周期,速さの関係より,\[ V = \bun{\lambda}{T} \quad\therefore T = \bun{\lambda}{V} \cdots\cdots\maru{2} \]であるから, $\maru{2}$ 式を $\maru{1}$ 式に代入して,\[V = \bun{g T}{2\pi} = \bun{g}{2\pi}\bun{\lambda}{V} \\ \therefore \color{red}{ V = \kon{\bun{g \lambda}{2\pi}} } \] となる。これが重力波の伝わる速さであり,波長が大きい波ほど速く伝わるが,水深には無関係であることが分かる。
戻る