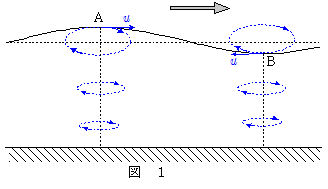
しかし水深が波長に比べて浅くなると(または,水深に比べて波長が長いと),水の動きは水面近傍にとどまらず水深の深くにまで及ぶようになる。また水の動きも円ではなく,水平方向につぶれた楕円形になっていく(図1参照)。(図1で,山の部分 $\mathrm{A}$ と谷の部分 $\mathrm{B}$ では,水の速度は大きさが等しく,向きは逆になっていることに留意。)
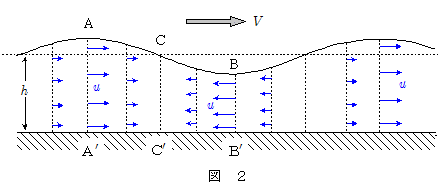
その極限として,水面から水底までの水全体が,上下方向の運動が極めて小さくなった状態,すなわちほとんど水平方向に運動している場合を考える(図2)。
さらに図2のように,鉛直方向にみたとき水底から水面まで,同一鉛直面内の水はすべて同じ速度で運動していると仮定する。もちろんその速度は場所によって異なり,1波長ごとに周期的に変化しているものとする。この仮定の下では,たとえば山の部分 $\mathrm{AA'}$ での水の速さを $u$ とすれば谷の部分 $\mathrm{BB'}$ での水の速さも $u$ であり,向きは互いに逆向きになっていることになる。このように,水の速度分布は,水の基準面位置(変位ゼロの位置)を通る鉛直面 $\mathrm{CC'}$ に関して対称になっており,このような分布を1波長ごとに繰り返した状態を保ちつつ,波の移動とともにこの速度分布全体が波の進行方向側にずれていく・・・・,このような状況をイメージすればよい。
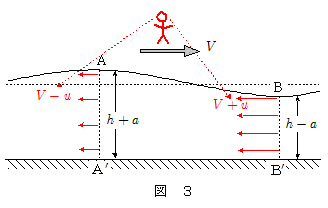
ここでこの波を,波の伝わる速さ $V$ で移動する観測者が観測したとする(図3の赤で示した人)。
いま,山の部分の断面 $\mathrm{AA'}$ ,谷の部分の断面 $\mathrm{BB'}$ での水の速さを $u$ とする。ただし,向きは互いに逆向きになっている。このときこの観測者から見ると,波はこの観測者に対して静止しており,水は,山の部分では $V-u$ の速さで,谷の部分では $V+u$ の速さで,ともに同じ向きに動いているように見えることになる。
水の基準面の高さを水底から測って $h$ とし,波の上下方向の変位の振幅を $a$ とする。ただし $a \ll h$ とし,水の上下方向の運動量はきわめて小さいものとする。
まず,水の質量保存の立場から,次の関係が導かれる。
山の部分 $\mathrm{AA'}$ に高さ $h+a$ ,奥行き $1$ の,また谷の部分 $\mathrm{BB'}$ に高さ $h-a$ ,奥行き $1$ の鉛直面を,流れに垂直な向き (この紙面に垂直な向き) に考える。これらの鉛直面の面積はそれぞれ $(h+a)\times 1$ , $(h-a)\times 1$ である。
流速 $v$ の液体の流れがあるとき,この流れに垂直な面積 $S$ の面を単位時間に通過していく液体の質量は $密度 \times S \times v$ で与えられる。
よって本題の場合,速さ $V$ で運動するこの観測者から見ると,それぞれの鉛直断面を単位時間に通過していく水の量は,水の密度を $\rho$ として,山の部分 $\mathrm{AA'}$ で $\rho \times (h+a)\times 1 \times (V - u)$ ,谷の部分 $\mathrm{BB'}$ で $\rho \times (h - a)\times 1 \times (V + u) $ と表される。水の湧き出しなどがない限り 山 $\mathrm{AA'}$ ~谷 $\mathrm{BB'}$ の区間の水量は一定しているはずであるから,出ていった水の量だけ水が入ってきたことになる。よって,次式が成り立つ。\[\quad 単位時間について, \\ \quad \mathrm{AA'} からの流出量 = \mathrm{BB'} からの流入量 \\ \therefore \rho \times (h + a)\times 1 \times (V - u) = \rho \times (h - a)\times 1 \times (V + u) \\ \kern-1em \therefore (h + a) (V - u) = (h - a) (V + u) \\ \kern-1em \therefore h u = a V \\ \kern-1em \therefore u = \bun{a V}{h} \cdots\cdots \maru{1} \] つぎに,水面の流線に沿って流れる単位体積あたりの水について,この観測者から見たエネルギー保存を考える。(本来は大気圧の影響も考慮する必要があるが,水面付近での大気圧の変化は無視できる。)
重力加速度を $g$ として,\[\bun{1}{2} \rho (V - u)^2 + \rho g a = \bun{1}{2} \rho (V + u)^2 - \rho g a \\ \kern-1em \therefore 2 g a = 2 V u \cdots\cdots\maru{2} \] $\maru{1}$ 式を $\maru{2}$ 式に代入して $u$ を消去すると,\[g a = V\times \bun{a V}{h} \\ \kern-1em \therefore \quad \color{red}{ V = \kon{g \, h} \quad(浅水波の速さ) } \]
以上のように,浅水波の速さは波の波長にはよらず,水深によって変化し,水深が深いほど速くなる。
津波は深い海洋を伝わってくる波であるが,津波の波長は数十キロから数百キロもあり,数千m程度の海洋の深さは波長に比して十分に浅いことになり,津波は概ね浅水波として扱うことができる。したがってその速さは上式を使って求めることができ,水深5000mほどの海洋では時速800キロほどにもなり,これはジェット機の速さに匹敵する。水深500mほどの海洋では時速250キロでこれは新幹線並み,水深10mで時速35キロ,これは街中を走る自動車の速度ほどである。
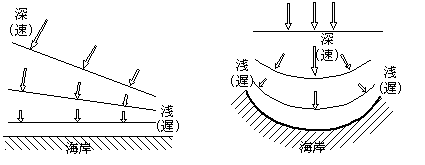
また,海岸に打ち寄せる波は海岸線に近づくにつれて海岸線に平行になっていくが,これは海岸線に近いほど水深が浅くなっているために波の速さが遅くなり,海岸線に近い波は沖合いの波を待っているような形になるために起きる現象である。
戻る