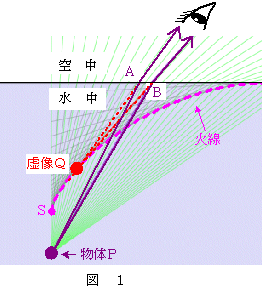
図1は,水中の物体Pを空気中から見た場合,像(虚像)Qがどこにできるかを示しています。
物体Pから出た光は四方八方にに広がっていきますが,水面で屈折(臨界角以上では全反射)し,その一部の光が観測者の「眼」に届きます。上図で薄緑色の光線群は,物体Pからでた光線を表しています。
いま水面上の点A,点Bを通った光線が観測者の「眼」に届いたとします。 A~B 間の間隔はごく狭い(小さい値)でしょうから,この区間を通った光線は観測者の「眼」にはすべて1点 Q から出てきた光線のように届きます。すなわちこの点 Q に物体があるかのように見えることになり,これが観測者がこの位置から見たときに見える物体Pの「虚像Q」ということになります。
このように,物体Pから出た光線のうち,ごく近接した光線の交点の位置に虚像ができることになります。
然るに観測者が見る位置を変えれば『眼』に届く光線も違ってくるわけで,近接した光線の交点の位置もずれてきます。これが,観測者がどの位置から水中を観るかによって像の位置が変わってくる理由です。
虚像の位置は,実際の物体の位置より観測者に近づいて見えます。つまり,浮き上がって,かつ手前側(観測者に近い側)に見えることになります。
点Sは,物体Pを真上から覗き込んだときの虚像のできる位置です。空気の屈折率を $1$ ,水の屈折率を $n\,\,(\, \gt \,1\,)$ ,物体P,虚像Qの水面からの深さをそれぞれ $h$ , $h'$ とすると,\[h' = \bun{h}{n} \]の関係があります。導出過程は こちら(真上から見たとき) (←入試の「浮き上がり」問題での基本形) です。
**********************
【火 線】
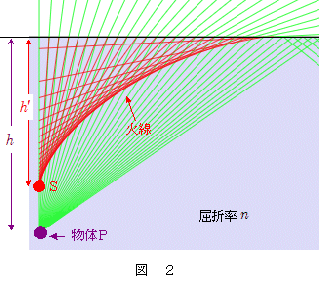
上図2の緑色の線は物体Pから出た光線群,また赤色の直線群は水面で屈折した光線をそれぞれ水中側に延長したものです。これらの延長線は互いに接し合うようにして重なり合っており,その部分が濃い赤色の曲線のようになって見えます。このように屈折光線群や反射光線群(本稿では延長線)が接するように重なりがずれていくとき,これらの光線群の包絡線を 火線 と言います(3次元の場合は面になります―(火面))。
物体Pの虚像Qはこの火線(火面)上にできます。なぜなら,この場合,虚像は近接光線同士の交点にできるのですから,当然と言えます。
したがって観測者が水中を覗き込む位置を変えたとき,虚像Qは火線上に沿って移動することになります。
**********************
次に,水中から空気中の物体を見たときについて考えてみましょう。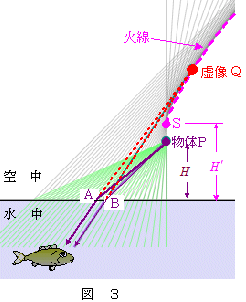
この場合の虚像の位置は,実際の物体の位置より遠ざかって見えることになります。つまり,水面からの高さは実際の高さより高く,水平方向にもより遠ざかって見えることになります。
点Sは,物体Pの真下の水中からPを見たときに見える虚像の位置を表します。この場合虚像Qの水面から高さ $H'$ は,物体Pの水面からの高さを $H$ ,水の屈折率を $n$ として,\[H'= n\, H \]となり,空気中から水中を見たときと逆の関係になります。
◎屈折による像の歪み:
下図は,プールサイドから水面を見たとき,プール底がどのように見えるかを数学ソフト(Mathematica)で描き,これをなぞったものです。青い太線が観測者から見えるプール底です。もちろん,実際のプール底 は平面です。水深は $1\,\mathrm{m}$ ,水面から測った眼の高さは $2\,\mathrm{m}$ ,水の屈折率は $1.33$ として計算してあります。
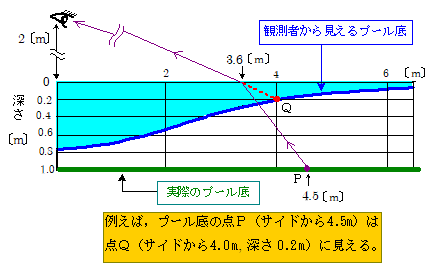
プール底は遠くほど浮き上がったように湾曲して見えますが,プールサイドから水平に $3\,\mathrm{m}$ 辺りから湾曲の仕方が下に凸から上に凸の形に変化しているのが読み取れます。もちろんその見え方は,観測者の目の高さによっても,またプールの水深によっても違ってきます。
下図は,水面から高さ $0.2\,\mathrm{m}$ ( $20\,\mathrm{cm}$ )の位置からプール底を見た図です。プール底は大きく歪んで袋状となり,眼の位置から水平に $1\,\mathrm{m}$ ほど超えたあたりからプール底はほとんど水面すれすれに見えることになります。さらに眼の高さを水面に近づけると,プール底は,上部を閉じ口にした形の袋状(ギリシャ文字のオメガ(Ω)をひっくり返したような感じ)に見える計算になります。
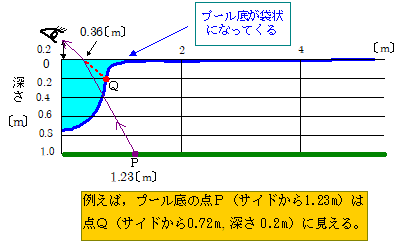
このように,水中を覗き込んで水中の物体を見たとき,大きさの無視できない物体の像は多少なりとも歪んで見えることになります。その理由は,観測者の視点と物体との距離によって像の浮き上がり方,近づき方の割合が一定していないからです。
詳しい計算式については「計算の詳細」を参照してください。
蛇足の話:
水中にある物体は浮き上がって見えるため,空気中から観ると正しい位置がつかめないことになります。
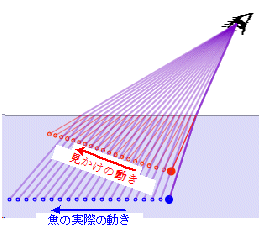
例えば,仮に魚が水平に泳いで観測者から遠ざかっているとしても,観測者が見ると魚は水面近くに浮き上がってきたように見えることになります。捕まえようとしたら,実は魚は大分遠くまで行ってしまっていた・・・ナンてことになるやもしれません(^^)。ちょっと面白いですね・・・?
シミュレーションへ戻る
真上から見たとき
計算の詳細