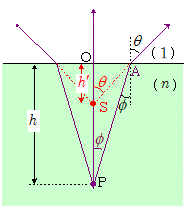
上図のように,物体Pの真上から見たとき虚像が点Sに見えたとします。このとき眼に入射する光線のうち,PAと直進する光線PSOについて考えます。
水の屈折率を $n$ ,空気の屈折率を $1$ とし, $\overline{\mathrm{PO}} = h$ , $\overline{\mathrm{SO}} = h'$ とします。
まず光線PAの点Aにおける入射角,屈折角をそれぞれ $\phi$ , $\theta$ とすると,屈折の法則より,\[n\sin\phi = \sin\theta \quad \cdots \cdots\maru{1}\]
一方,△POAと△SOAに着目すると,辺OAが共通であることに注目して,\[\overline{\mathrm{OA}}= \overline{\mathrm{PO}}\times \tan\phi = \overline{\mathrm{SO}}\times \tan\theta \\ \kern-1em \therefore h \times \tan\phi = h' \times \tan\theta \quad \cdots \cdots\maru{2}\]
ここでPの真上から見ているのだから,入射角 $\phi$ ,屈折角 $\theta$ は十分に小さい値と考えてよいでしょう。よって以下の近似式が成り立つとします。\[ \sin\phi \kinji \tan\phi \kinji \phi \\ \sin\theta \kinji \tan\theta \kinji\theta\]
上記の近似を $\maru{1}$ 式, $\maru{2}$ 式に適用すると,\[n \times \phi \kinji \theta \quad \cdots \cdots\maru{1}' \\ h \times \phi \kinji h' \times \theta \quad \cdots \cdots\maru{2}' \] $\maru{1}' \div \maru{2}'$ より,\[\bun{n}{h} = \bun{1}{h'} \\ \kern-1em \therefore h' = \bun{h}{n} \]