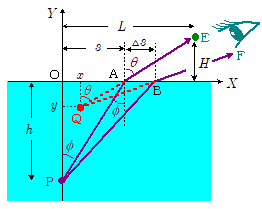
上図において,座標 $(\,0,\,\,-h\,)$ にある物体Pを座標 $(\,L,\,\,H\,)$ の点Eから見たとき,座標 $(\,x,\,\,y\,)$ の点Qにその像が見えたとします。ただし $x\,\gt \,0\,$,$y\,\lt \,0\,$ とし,また水の屈折率を $n\,(\,\gt 1\,)$ ,空気の屈折率を $1$ とします。
水面上の点A $(\,s,\,\,0\,)$ を通る光線PAEの水面での入射角,屈折角をそれぞれ $\phi$ , $\theta$ とすると,屈折の法則により,\[n\,\sin\phi = \sin\theta \quad\cdots\cdots\maru{1}\]が成り立ちます。
像ができる位置Qは,光線PAEに近接する光線との交点だから,点Aより微小距離 $\varDelta s$ だけ離れた点Bを通る光線PBFを考え,この光線の水面での入射角,屈折角をそれぞれ $\phi + \varDelta \phi$ , $\theta +\varDelta \theta$ とします。ただし $\phi \gg | \varDelta \phi |$ , $\theta \gg | \varDelta \theta |$ とする。
まず△ $\mathrm{Q}x\mathrm{A}$ に着目すると,\[\overline{x\mathrm{A}} = \overline{x\mathrm{Q}} \cdot \tan\theta \\ \kern-1em \therefore (s-x) = |y|\,\tan\theta = |y|\,\bun{\sin\theta}{\cos\theta} \\ \kern-1em \therefore (s-x)\,\cos\theta = |y|\,\sin\theta \quad \cdots\cdots \maru{2} \] 同様に△ $\mathrm{Q}x\mathrm{B}$ に着目して,\[\overline{x\mathrm{B}} = \overline{x\mathrm{Q}} \cdot \tan(\theta + \varDelta \theta) \\ \kern-1em \therefore (s + \varDelta s - x) = |y|\,\tan(\theta +\varDelta \theta) \\ \kern-1em \therefore (s + \varDelta s - x)\,\cos(\theta + \varDelta \theta) = |y|\,\sin(\theta + \varDelta \theta) \quad \cdots\cdots \maru{3} \] $\sin(\theta + \varDelta \theta)$ ,$\cos(\theta + \varDelta \theta)$ を展開し,さらに $\sin(\varDelta \theta) \kinji \varDelta \theta$ , $\cos(\varDelta \theta) \kinji 1$ の近似式の適用,および2次の微少量 $\varDelta s\cdot \varDelta \theta$ を無視すると, 上式は,\[\kern-2em (s-x)\cos\theta-(s-x)\sin\theta\cdot\varDelta \theta +\varDelta s\cdot\cos\theta \\ \kern 8em \kinji |y|\sin\theta + |y|\cos\theta\cdot\varDelta \theta \quad\cdots\cdots\maru{3}'\] 上式に $\maru{2}$ 式を代入して整理すると,\[-(s -x) \sin\theta\cdot \varDelta \theta + \varDelta s \cdot\cos\theta = |y|\cos\theta\cdot \varDelta \theta \] さらに右辺の $y$ に $\maru{2}$ 式を代入して $y$ を消去し整理すると,\[-(s -x) \sin\theta\cdot \varDelta \theta + \varDelta s \cdot\cos\theta = (s-x)\bun{\cos^2\theta}{\sin\theta}\cdot \varDelta \theta \\ \kern-1em \therefore \varDelta s \cdot\cos\theta = \bun{s - x}{\sin\theta}\varDelta \theta \] $\bun{\varDelta s}{\varDelta \theta}$ の極限を考えると微分 $\displaystyle{\dif{s}{\theta}}$ となるので,上式より,\[x = s - \dif{s}{\theta}\cdot \sin\theta\cdot\cos\theta \quad\cdots\cdots\maru{4} \] を得る。この $x$ を $\maru{2}$ 式に代入して $|y|$ を得る。\[|y| = (s-x)\bun{\cos\theta}{\sin\theta} \\ \kern 1em = \dif{s}{\theta}\cdot \cos^2\theta \quad \cdots\cdots\maru{5} \] 次に, $\displaystyle{\dif{s}{\theta}}$ を求め, $\maru{4}$ 式, $\maru{5}$ 式に代入していくことを考えます。
まず,前図において,△POAに着目すると,\[\overline{\mathrm{OA}} = \overline{\mathrm{PO}} \cdot \tan\phi \\ \kern-1em \therefore s = h\cdot \tan\phi \] 上式を両辺微分して,\[\mathrm{d}s = h\cdot \bun{\mathrm{d}\phi}{\cos^2\phi} \\ \kern-1em \therefore \dif{s}{\phi} = \bun{h}{\cos^2\phi} \quad \cdots\cdots\maru{6} \] 一方,屈折の法則 $\maru{1}$ 式を両辺微分すると,\[n\,\cos\phi\cdot \mathrm{d}\phi = \cos\theta\cdot \mathrm{d}\theta \\ \kern-1em \therefore \dif{\phi}{\theta} = \bun{\cos\theta}{n\,\cos\phi} \quad \cdots\cdots\maru{7} \] $\maru{6}$ 式と $\maru{7}$ 式とより,\[\dif{s}{\theta} = \dif{s}{\phi}\cdot \dif{\phi}{\theta} \\ \kern1.5em = \bun{h}{\cos^2\phi}\cdot \bun{\cos\theta}{n\,\cos\phi} \\ \\ \kern1.5em = \bun{h\cdot\cos\theta}{n\,\cos^3\phi} \] これを $\maru{4}$ 式, $\maru{5}$ 式に代入して, $x$ , $y$ を求める。\[x = s - \dif{s}{\theta}\cdot \sin\theta\cdot\cos\theta \\ \kern1em = s - \bun{h\cdot\cos\theta}{n\,\cos^3\phi}\cdot \sin\theta\cdot \cos\theta \] ここで $s = h \,\tan\phi = h\bun{\sin\phi}{\cos\phi}$ , $\sin\theta = n\,\sin\phi$ (← $\maru{1}$ 式)の関係を上式に代入して,\[x = h\bun{\sin\phi}{\cos\phi} - \bun{h}{\color{red}{\cancel{\color{black}{n}}} \,\cos^3\phi}\cdot \color{red}{\cancel{\color{black}{n}}}\,\sin\phi\cdot \cos^2\theta \\ \kern1em = \bun{h\cdot \sin\phi}{\cos^3\phi}\big\{\cos^2\phi - (1 - \sin^2\theta) \big\}\\ \kern1em = \bun{h\cdot \sin\phi}{\cos^3\phi}\big\{\cos^2\phi - (1 - n^2\sin^2\phi) \big\} \\ \kern1em = \bun{h\cdot \sin\phi}{\cos^3\phi}\big\{\cos^2\phi - 1 + n^2\sin^2\phi) \big\} \\ \kern1em = \bun{h\cdot \sin\phi}{\cos^3\phi}\big\{- \sin^2\phi + n^2\sin^2\phi) \big\} \\ \kern1em = \bun{h\cdot \sin\phi}{\cos^3\phi}\cdot (n^2 - 1) \sin^2\phi \\ \kern1em = h\,(n^2 - 1)\cdot\tan^3\phi \quad \cdots\cdots\maru{8}\] また $\maru{5}$ 式より,\[|y| = \dif{s}{\theta}\cdot \cos^2\theta \\ \kern1em = \bun{h\cdot\cos\theta}{n\,\cos^3\phi}\cdot \cos^2\theta \\ \kern1em = \bun{h}{n}\bun{\cos^3\theta}{\cos^3\phi} \\ \kern1em = \bun{h}{n}\bun{\bigg(\kon{1 - n^2\sin^2\phi}\bigg)^3}{\cos^3\phi} \quad \cdots\cdots\maru{9}\]
◎2点P,Eを結ぶ屈折光線と水面との交点:
$\maru{8}$ 式, $\maru{9}$ 式が虚像Qの座標 $x$ , $y$ を与える式ですが,角 $\phi$ がまだ求められていません。角 $\phi$ は,物体Pと眼Eの2点を結ぶ光線PAEの水面での入射角ですので,角 $\phi$ を知るには点Aの $x$ 座標 $s$ が分かれば, \[\phi = \tan^{-1}\bigg(\bun{s}{h}\bigg)\]より $\phi$ が分かることになります。ここで上式の意味は, $\phi$ は\[ \tan\phi=\bun{s}{h} \] という式をを満たす値ですヨ・・・ということを表します。
では $s$ はどうすれば求まるか?
$s$ は,2点P,E間の水平距離 $L$ ,水面までの垂直距離 $h$ , $H$ が与えられたとき,両点を結ぶ屈折光線の水面上の通過点を与えるものです。
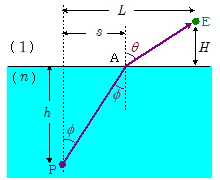
そこでまず,屈折の法則を $h$ , $H$ , $L$ , $s$ を使って表してみましょう。\[n\,\sin\phi = \sin\theta \\ \kern-1em \therefore n\,\bun{s}{\kon{h^2 + s^2}} = \bun{L - s}{\kon{H^2 + (L- s)^2}} \\ \kern-1em \therefore n^2\, s^2 \big\{ H^2 + (L - s)^2 \big\} = (L - s)^2 \cdot (h^2 + s^2 )\] 上式は $s$ について4次方程式になりますので,これを解くのは簡単ではありません。本シミュレーションではフェラリーの方法と呼ばれる解法にもとづくプログラムを組み, $s$ を求め,さらに $\phi$ を計算しています。その解法自体は数学の話になりますので,説明は省きます(かなり面倒な計算過程になります)。
以上のように,像Qの位置座標 $x$ , $y$ は $\maru{8}$ 式, $\maru{9}$ 式では入射角 $\phi$ を媒介変数として表されましたが,その $\phi$ 自身は2点P・Eを結ぶ屈折光線の水面上の交点座標 $s$ で決まるわけですから,結局,2点P,Eが与えられればQの位置座標 $x$ , $y$ は自動的に決まってしまうことになります。この $x$ と $y$ の関係で与えられる曲線が前項で述べた『火線』ということになります。
シミュレーションへ戻る
概 要