行列の標準形
(舞台設定)
R:実数をすべて集めた集合(実数体)
A:(m,n)型実行列
(主張の確認)
(m,n)型実行列Aは、どのようなものでも、基本変形のみを用いて、次の形の標準形に変形できる。
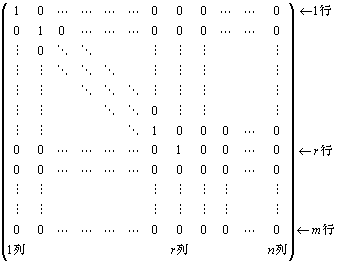
この標準形は、(1,1)成分, (2,2)成分, …, (r,r)成分というr個の成分だけが1、
そのほかの成分はすべて0
という行列。
(証明) [斎藤『線形代数入門』2章§4定理4.2(pp.50-51);砂田『行列と行列式』§4.2定理4.11(pp.144).]
次の手順にしたがうことで、基本変形だけで、あらゆる行列を標準形に至らせることができる。
なお、ここでは、(m,n)型実行列Aがm>nである場合に、Aを標準形に至らせる手順のみを取りあげる。
Step0:
(m,n)型実行列Aが、零行列であるか否かをチェック。
(i) (m,n)型実行列Aが、零行列であるケース
→Aは、もともと、標準形である。1になっている成分の個数(rankA)=0]。
(ii)(m,n)型実行列Aが、零行列ではないケース
→step1へ進む。
Step1:
Step1-1:下図のように、(m,n)型実行列Aの(1,1)成分が0であるならば、

列の入れ替えを行う列基本変形type2 と、
行の入れ替えを行う行基本変形type2 だけを用いて、
(m,n)型実行列Aの(1,1)成分に、非0を持ってくる。
Step1-2:(m,n)型実行列Aの(1,1)成分を要として第1行を掃き出す。
それから、(m,n)型実行列Aの(1,1)成分を要として第1列も掃き出す。
その結果、次のかたちが得られる。

※具体的には?→詳細
※「掃き出す」とよばれる変形は、基本変形のみの組み合わせであることに注意。
Step1-3:(m,n)型実行列Aから、第1行・第1列を取り去った残りの(m−1,n−1)型行列が、
零行列であるか否かをチェック。
(i) (m−1,n−1)型実行列が零行列であるケース
→Aは標準形に到達。1になっている成分の個数(rankA)=1。
確かに、基本変形だけで標準形に到達している。

(ii) (m−1,n−1)型実行列が零行列ではないケース
→step2へ進む。
Step2:
Step2-1:下図のように、(m,n)型実行列Aの(2,2)成分が0であるならば、

列基本変形type2を用いた、第2列と第3列〜第n列との入れ替え
行基本変形type2を用いた、第2行と第3行〜第m行との入れ替え
だけによって、
Aの(2,2)成分に非0を持ってくる。
Step2-2:(m,n)型実行列Aの(2,2)成分を要として第2行を掃き出す。
それから、(m,n)型実行列Aの(2,2)成分を要として第2列も掃き出す。
すると、次のかたちが得られる。

※具体的には?→詳細
※「掃き出す」とよばれる変形は、基本変形のみの組み合わせであることに注意。
Step2-3:(m,n)型実行列Aから、
第1行・第2行・第1列・第2列を取り去った残りの(m−2,n−2)型実行列が、
零行列であるか否かをチェック。
(i) (m−2,n−2)型実行列が零行列であるケース

→Aは標準形に到達。1になっている成分の個数(rankA)=2。
確かに、基本変形だけで標準形に到達している。
(ii) (m−2,n−2)型実行列が零行列ではないケース
→step3へ進む。
Step3:
:
:
:
Step (n-1):
Step (n-1)-1:(m,n)型実行列Aの( n−1,n−1)成分が0であるならば、


列基本変形type2を用いた、第(n-1)列と第n列との入れ替え
行基本変形type2を用いた、第(n-1)行と第n行〜第m行との入れ替え
だけによって、
Aの( n−1,n−1)成分に、非0を持ってくる。
Step(n-1)-2:(m,n)型実行列Aの( n−1,n−1)成分を要として第(n-1)行を掃き出す。
それから、(m,n)型実行列Aの( n−1,n−1)成分を要として第(n-1)列も掃き出す。

※具体的には?→詳細
※「掃き出す」とよばれる変形は、基本変形のみの組み合わせであることに注意。
Step(n-1)-3:(m,n)型実行列Aから、
第1行〜第(n-1)行・第1列〜第(n-1)列を取り去った残りの(m−n+1,1)型実行列が、
零行列であるか否かをチェック。
(i) (m−n+1,1)型実行列が零行列であるケース

→Aは標準形に到達。1になっている成分の個数(rankA)=n-1。
確かに、基本変形だけで標準形に到達している。
(ii) (m−n+1,1)型実行列が零行列ではないケース
→stepnへ進む。
Step n:
Step n-1:(m,n)型実行列Aの( n,n)成分が0であるならば、

行基本変形type2を用いた、第n行と第(n+1)行〜第m行との入れ替え
だけによって、
Aの( n,n)成分に、非0を持ってくる。
Step n-2:(m,n)型実行列Aの( n,n)成分を要として第n列を掃き出す。
※具体的には?→詳細
※「掃き出す」とよばれる変形は、基本変形のみの組み合わせであることに注意。
すると、次の標準形に到達する。

1になっている成分の個数(rankA)=n。
確かに、基本変形だけで標準形に到達している。












