|
解説:ここで定義した関数列についての、詳しい説明。 |
|
|
ここでは、この定理のなかで [性質1]-[性質3]を満たすと主張される関数列の定義を、具体的に展開して説明する。 → Step1:f1の定義 → Step1-2:f2の定義 → Step1-3:f3の定義 : → Step1-n:fnの定義 : |
|
|
→ 定理「非負有界1変数関数に一様収束する単関数列」に戻る→定理「非負1変数関数に各点収束する単関数列」に戻る |
|
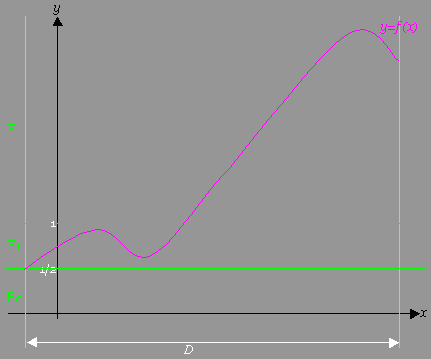
[図例]
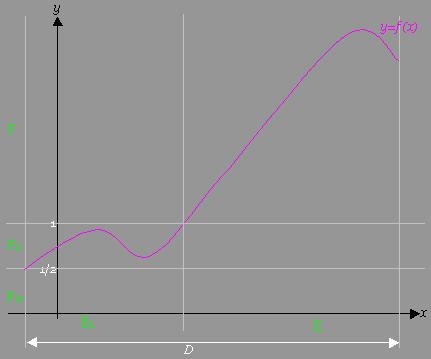
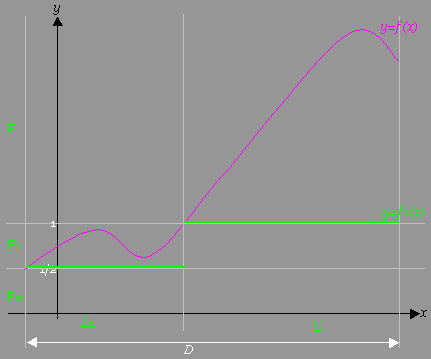
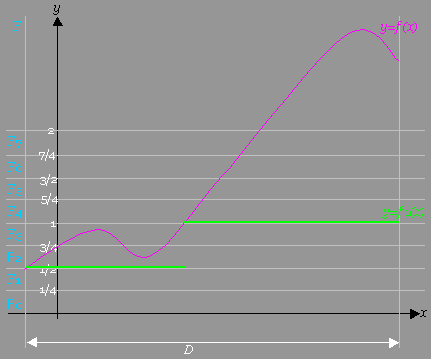
[図例]
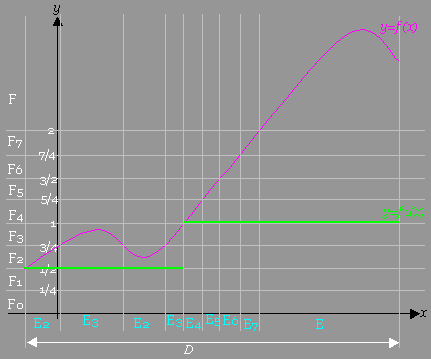
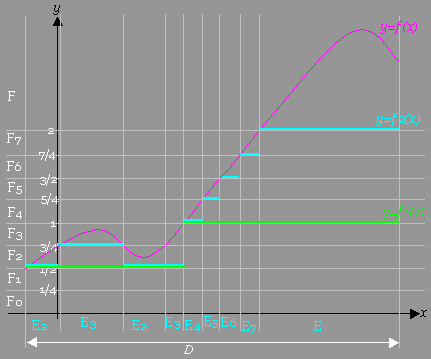
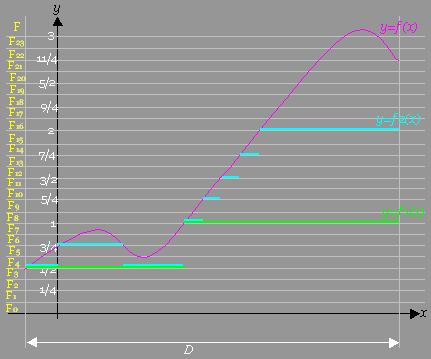
[図例]
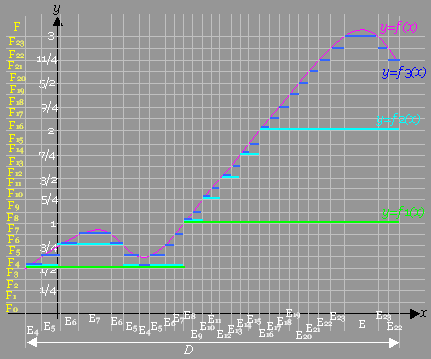
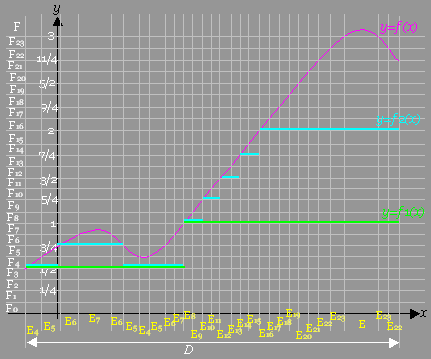 [手順3]上記のR上の点集合E0, E1 , E2 ,…, E23 , E の定義関数を用いて、次のように、f3を定義する。
[手順3]上記のR上の点集合E0, E1 , E2 ,…, E23 , E の定義関数を用いて、次のように、f3を定義する。 [case 0] x∈E0ならば、f3 (x)=0
[図例]
→
f3の定義の冒頭に戻る[case 0] 0/2n≦f (x) < 1/2n を満たすx∈Dに対して、fn (x) =0
[case 0] x∈E(n,0)ならば、fn (x)=0
→
fnの定義の冒頭に戻る|
|