◎本シミュレーションについて：

　２次元媒質として，上の図３のような網目状の広がりの各格子点に，質量 $m$ の微小粒子が結び付けられているものを考える。網目は間隔 $l$ の正方形状であり，この間隔は粒子が運動しても変わらないとする。粒子間には一定力 $S$ がはたらき，それぞれの粒子は互いに隣接する粒子からのみ力を受ける。粒子の運動はこの網目に垂直な方向に限られ，その変位は $l$ に比べて十分に小さいとする。
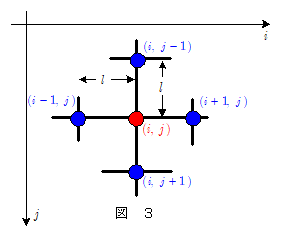
　以下，原点から数えて横に $i$ 番目，縦に $j$ 番目の粒子は $(i,\, j\,)$ のように記すこととする。
　いま粒子 $(i,\, j\,)$ に注目し，その変位を $\phi_{i,j}$ ，加速度を $a_{i,j}$ とする。

　このときこの粒子が $i$ 方向に隣接する $(i-1,\, j)$ ， $(i+1,\, j)$ の粒子から受ける $\phi$ 方向の力は，となりの粒子と結ぶ線分が $i$ 軸となす角を図４のように $\theta{}\,'$ ， $\theta$ とすると，それぞれ\[ -S\, \sin\theta\,' \\ S\, \sin\theta \] である。ここで変位は $l$ に比べて十分に小さいとの仮定から $\theta\,'$ ， $\theta$ も十分に小さい値であり，以下の近似が成り立つ。\[ -S\, \sin\theta\,' \kinji -S\, \tan\theta\,' \\ \quad\quad\quad\quad = -S\times \bun{\phi_{i,j} - \phi_{i-1,j} }{l} \\ \quad\quad\quad\quad = -\bun{S}{l}\times (\phi_{i,j} - \phi_{i-1,j}\,) \\ \quad S\, \sin\theta \kinji S \, \tan\theta \\ \quad\quad\quad\quad = S\times\bun{\phi_{i+1,j} - \phi_{i,j} }{l} \\ \quad\quad\quad\quad = -\bun{S}{l}\times (\phi_{i,j} - \phi_{i+1,j}\,) \] 　同様に $j$ 方向に隣接する粒子 $(i,\, j-1)$ ， $(i,\, j+1 \,)$ から受ける $\phi$ 方向の力は，それぞれ\[-\bun{S}{l}\times (\phi_{i,j} - \phi_{i,j-1}\,) \\ -\bun{S}{l}\times (\phi_{i,j} - \phi_{i,j+1}\,) \]となる。これらの力を受けて粒子 $(i,\, j)$ は加速度 $a_{i,j}$ を生じるのであるから，その運動方程式は，\[m \, a_{i,j}= -\bun{S}{l}\times (\phi_{i,j} - \phi_{i-1,j}\,) \\ \quad\quad\quad -\bun{S}{l}\times (\phi_{i,j} - \phi_{i+1,j}\,) \\ \quad\quad\quad -\bun{S}{l}\times (\phi_{i,j} - \phi_{i,j-1}\,) \\ \quad\quad\quad -\bun{S}{l}\times (\phi_{i,j} - \phi_{i,j+1}\,) \\ \quad\quad =-\bun{S}{l}\{4\phi_{i,j}-(\phi_{i-1,j}+\phi_{i+1,j}) - (\phi_{i,j-1}+ \phi_{i,j+1}\,) \} \cdots\cdots\maru{6} \]となる。
　いま，時刻 $t$ における粒子 $(i,\, j)$ の変位 $\phi_{i,j}$ が\[\phi_{i,j}=A\sin(2\pi f \,t) \]であるとする。ここで $f$ は振動数， $A$ は振幅である。全粒子は互いに結ばれているのであるから，振動数は $f$ に等しく，また全粒子の振幅も $A$ とする。また， $i$ 方向， $j$ 方向の波の位相速度をそれぞれ $w_x$ ， $w_y$ とすると，隣接する粒子の時刻 $t$ における変位は以下のようになる。\[ \phi_{i-1,j}=A\sin2\pi f\bigg(t + \bun{l}{w_x}\bigg) \\ \phi_{i+1,j}=A\sin2\pi f\bigg(t - \bun{l}{w_x}\bigg) \\ \phi_{i,j-1}=A\sin2\pi f\bigg(t + \bun{l}{w_y}\bigg) \\ \phi_{i,j+1}=A\sin2\pi f\bigg(t - \bun{l}{w_y}\bigg)\]　ここで，$ \sin\alpha + \sin\beta = 2\cos\bun{\alpha-\beta}{2} \cdot \sin\bun{\alpha+b}{2}$ の公式を利用すると，\[\phi_{i-1,j} + \phi_{i+1,j}=A\sin2\pi f\bigg(t + \bun{l}{w_x}\bigg) + A\sin2\pi f\bigg(t - \bun{l}{w_x}\bigg) \\ \quad\quad\quad\quad = 2A\, \cos\bigg(\bun{2\pi f \,l}{w_x}\bigg) \times \sin 2\pi f \,t \\ \quad\quad\quad\quad = 2\, \cos\bigg(\bun{2\pi f \,l}{w_x}\bigg) \times \phi_{i,j} \\ \phi_{i,j-1} + \phi_{i,j+1}=A\sin2\pi f\bigg(t + \bun{l}{w_y}\bigg) + A\sin2\pi f\bigg(t - \bun{l}{w_y}\bigg) \\ \quad\quad\quad\quad = 2A\, \cos\bigg(\bun{2\pi f \,l}{w_y}\bigg) \times \sin 2\pi f \,t \\ \quad\quad\quad\quad = 2\, \cos\bigg(\bun{2\pi f \,l}{w_y}\bigg) \times \phi_{i,j} \]　これらを $\maru{6}$ 式に代入すると，\[m \, a_{i,j}= -\bun{S}{l}\{4\phi_{i,j}-(\phi_{i-1,j}+\phi_{i+1,j}) - (\phi_{i,j-1}+ \phi_{i,j+1}\,) \} \\ \quad\quad =-\bun{2S}{l}\bigg\{2 - \cos\bigg(\bun{2\pi f \,l}{w_x}\bigg) - \cos\bigg(\bun{2\pi f \,l}{w_y}\bigg)\bigg \}\times \phi_{i,j} \\ \quad\quad =-\bun{2S}{l}\bigg [ \bigg\{ 1 - \cos\bigg(\bun{2\pi f \,l}{w_x}\bigg)\bigg\} + \bigg\{ 1 - \cos\bigg(\bun{2\pi f \,l}{w_y}\bigg)\bigg\} \bigg ]\times \phi_{i,j} \]　さらに， $\cos\alpha=1-2\sin^2\bun{\alpha}{2}$　の公式を適用すると，上式は，\[m \, a_{i,j}=-\underline{\bun{4S}{l}\bigg \{\sin^2\bigg(\bun{\pi f \,l}{w_x}\bigg) + \sin^2\bigg(\bun{\pi f \,l}{w_y}\bigg) \bigg\} }\times \phi_{i,j} \] となる。上式の下線部は定数であるからこれを $K$ とおくと，\[m \, a_{i,j}=-K \times \phi_{i,j} \]となって，粒子 $(i,\, j)$ は単振動をすることがわかる。その角振動数 $\omega$ は，\[ \kern-1em \omega=\kon{\bun{K}{m}} \\ = 2\kon{\bun{S}{m\, l}}\kon{\sin^2\bigg(\bun{\pi f \,l}{w_x}\bigg) + \sin^2\bigg(\bun{\pi f \,l}{w_y}\bigg)} \]　 $i$ 方向，$j$ 方向にみた波長をそれぞれ $\lambda_x$ ， $\lambda_y$ とすると，波の振動数と波長，位相速度の関係より $w_x/f=\lambda_x$ ， $w_y/f=\lambda_y$　であり，粒子が十分に密に詰まっていれば粒子間隔 $l$ は $\lambda_x$ ， $\lambda_y$ に比べて十分に小さいと考えてよいので，\[ \bun{fl}{w_x}=\bun{l}{\lambda_x} \ll 1 \\ \bun{fl}{w_y}=\bun{l}{\lambda_y} \ll 1 \] である。よって $|\alpha| \ll 1$ のときの近似式 $\sin\alpha \kinji \alpha$ 　を適用すると，\[\kern-1em \omega = 2\kon{\bun{S}{m\, l}}\kon{\sin^2\bigg(\bun{\pi f \,l}{w_x}\bigg) + \sin^2\bigg(\bun{\pi f \,l}{w_y}\bigg)} \\ \kinji 2\kon{\bun{S}{m\, l}}\kon{\bigg(\bun{\pi f \,l}{w_x}\bigg)^2 + \bigg(\bun{\pi f \,l}{w_y}\bigg)^2 } \\ = 2\pi f\kon{\bun{S\, l}{m}}\kon{\bun{1}{w_x{}^2} + \bun{1}{w_y{}^2}} \]　波の伝播速度を $v$ とすると，前ページで説明したように， $w_x$ ， $w_y$ と $v$ の間には\[\bun{1}{v^2}=\bun{1}{w_x{}^2} + \bun{1}{w_y{}^2} \]の関係があった。また，角振動数 $\omega= 2\pi f$ であるから，上の関係式は以下のようになる。\[2\pi f = 2\pi f\kon{\bun{S\, l}{m}}\kon{\bun{1}{w_x{}^2} + \bun{1}{w_y{}^2}} \\ \therefore 1=\kon{\bun{S\, l}{m}}\kon{\bun{1}{v^2}} \\ \therefore \color{red}{v=\kon{\bun{Sl}{m}}} \]　（上式は，１次元媒質の場合（質点列上の横波）と同じ伝播速度の式と同じになっている。）

　

　ところで本シミュレーションの設定では，それぞれの網目に位置する各質点はいずれも隣接する計４個の正方形に共有されているので，一辺 $l$ の正方形の一つに属する質点の数は，\[ \bun{1}{4} 個分 \times 4 隅 = 1 個 \]となり，一辺 $l$ の正方形のそれぞれに含まれる質点の質量は $m$ となります。したがってこの２次元媒質の面密度 $\rho$ は，\[\rho = \bun{m}{l^2} \]と考えることができます。よって上式の $v$ は，\[v = \kon{\bun{S l}{m}} \\ \quad = \kon{\bun{S}{\bun{m}{l^2}l}} = \color{red}{\kon{\bun{S/l}{\rho }}\cdots\cdots \Maru{\mathrm{A}}} \]となり，波の速さは媒質の面密度に反比例することになる。

---

　　　前に戻る（２次元波の表し方） 　　　シミュレーションに戻る