弦を伝わる波のように1次元媒質を伝わる波の式は,例えば時刻 $t$ ,座標 $x$ における変位を $\phi$ として\[\phi=A\,\sin \, 2\pi \, f \bigg(t - \bun{x}{v}\bigg) \]のように,比較的簡単に表すことができる。ここで $A$ は波の振幅, $f$ は振動数, $v$ は波の伝播速度である。
しかし水面などのような2次元媒質を伝わる波の式となると,高校ではほとんど扱わない。どのよう式になるのだろうか。
本稿では,2次元波として,平面媒質上を山もしくは谷を結ぶ線が直線として表される波 ( 本稿では,以下この波を便宜的に平面波と記すことにします) がどのような式で表されるかについて考えてみる。
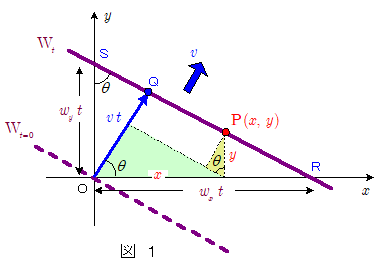
この波によって,原点O $(0, \, 0\,)$ の時刻 $t$ における変位 $\phi(0, \, 0,\, t)$ が\[\phi(0, \, 0,\, t)=A\sin(2\pi \, f \,t ) \quad\cdots\cdots\maru{1}\]のように時間変化しているものとする。
図1のように,時刻 $t=0$ に原点Oに差しかった波面 $\mathrm{W}_{t=0}$ が,時刻 $t$ に点P $(x, \, y\,)$ を通過したものとする。この波面を $\mathrm{W}_{t}$ とする。波面とは同じ位相を持つ面のことであるから,点Pにおける位相は,原点Oから波面 $\mathrm{W}_{t}$ に下した垂線の足Q $(x_\mathrm{Q}, \, y_\mathrm{Q}\,)$ の位相に等しい。すなわち,時刻 $t$ における点Pの変位 $\phi(x, \, y,\, t)$ を求めるには,時刻 $t$ における点Qの変位 $\phi(x_\mathrm{Q} , \, y_\mathrm{Q} ,\, t)$ を求めればよいことになる。
波は速さ $v$ で進んでいるのであるから,時間 $t$ の間に距離 $\overline{\mathrm{OQ}}=v\,t$ だけ進んでいる。
一方この波を $x$ 軸, $y$軸の方向に見ると,それぞれの軸方向に $v$ とは異なる速さで波が移動していくように見える。例えば時刻 $t=0$ に原点Oが波の山になっていたとすると,この山は $x$ 軸に沿って時間 $t$ の間に原点Oから点Rまで, $y$ 軸方向には原点Oから点Sまで進んだように見える。よって $x$ 軸, $y$ 軸に沿って移動していく波の速さをそれぞれ $w_x$ , $w_y$ とすると, $\overline{\mathrm{OR}}=w_x\, t$ ,$\overline{\mathrm{OS}}=w_y\, t$ であるから,上図の三角形 $\mathrm{ORQ}$ , $\mathrm{OSQ}$ において,\[\overline{\mathrm{OQ}}=\overline{\mathrm{OR}}\times \cos\theta \\ \therefore v\, t = w_x \, t\times\cos\theta \quad \therefore w_x=\bun{v}{\cos\theta}\quad(\ge v) \quad\cdots\cdots\maru{2}\\ \overline{\mathrm{OQ}}=\overline{\mathrm{OS}}\times \sin\theta \\ \therefore v\, t = w_y \, t \times\sin\theta \quad \therefore w_y=\bun{v}{\sin\theta} \quad(\ge v) \quad\cdots\cdots\maru{3} \]なる関係がある。上式から分かるように $w_x$ , $w_y$ は一般に波本来の伝播速度 $v$ より大きくなる。これは, $w_x$ , $w_y$ は「波面が $x$ 軸, $y$ 軸と交差する点が移動していく速さ」であって, 伝播速度 ${v}$ の ${x}$ 成分, ${y}$ 成分では ない からである。
例えば $\theta=0$ の場合,波は $x$ 軸方向に進む。このとき上式より $w_x=v$ , $w_y=\infty$ となるが,この場合波面は $x$ に垂直になっているのだから, O点が山になれば同じ $y$ 軸上のS点もその瞬間に山になる。O点の山が $y$ 軸に沿ってS点まで移動した…という考え方をするのであれば, $w_y=\infty$ でなければならないのは当然である。
O点の位相(山や谷といった状態)が速さ $w_x$ で $x$ 軸に沿って移動するのであるから, $w_x$ は $x$ 軸方向の位相速度と言える。同様に $w_y$ は, $y$ 軸方向の位相速度ということになる。
なお,伝播速度 $v$ の $x$ 成分 $v_x$ , $y$ 成分 $v_y$ は,もちろん\[v_x=v \, \cos\theta\quad(\le v) \\ v_y=v \, \sin\theta\quad(\le v) \]である。
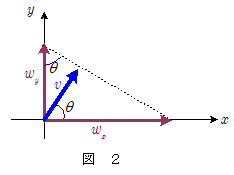
また $\maru{2}$ 式, $\maru{3}$ 式より,\[ \left \{ \begin{array}{rl} & \kern-1em \cos\theta=\bun{v}{w_x} \\ & \kern-1em \sin\theta=\bun{v}{w_y} \end{array} \right .\quad \therefore \tan\theta=\bun{\sin\theta}{\cos\theta}=\bun{w_x}{w_y} \\ また \cos^2\theta+\sin^2\theta=1 \quad であるから, \\ \bigg(\bun{v}{w_x} \bigg)^2 + \bigg(\bun{v}{w_y} \bigg)^2 = 1 \\ \therefore \bun{1}{v^2}=\bun{1}{w_x{}^2} + \bun{1}{w_y{}^2} \\ \therefore v=\bun{w_x\,w_y}{\kon{w_x{}^2+w_y{}^2}}\] の関係を得るが,この関係は, $v$ , $w_x$ , $w_y$ の関係を示す下図からも明らかである。
◎2次元波を式に表すと……:
原点Oの時刻 $t$ における変位 $\phi(0, \, 0,\, t)$ が\[\phi(0, \, 0,\, t)=A\sin(2\pi \, f \,t ) \quad\cdots\cdots\maru{1}\]で与えられる場合,時刻 $t$ における点P $(x, \, y\,)$ の変位 $\phi(x, \, y,\, t)$ がどのような式で表されるかについて考える。

先に述べたように,$\phi(x, \, y,\, t)$ は時刻 $t$ における点Qの変位 $\phi(x_\mathrm{Q} , \, y_\mathrm{Q} ,\, t)$ に等しい。一方時刻 $t$ における点Qの変位は,時刻 $t=0$ に原点にあった位相が距離 $\overline{\mathrm{OQ}}$ だけ伝わってきたものであるから,原点O $(0, \, 0\,)$ より時間的に $\bun{\overline{\mathrm{OQ}}}{v}$ だけ遅れた振動をしており,原点Oの時刻 $t - \bun{\overline{\mathrm{OQ}}}{v}$ の変位に等しい。よって,\[ \phi(x, \, y,\, t)=\phi(x_\mathrm{Q} , \, y_\mathrm{Q} ,\, t) \\ \quad\quad\quad\quad = \phi \bigg(0, \, 0,\, t-\bun{\overline{\mathrm{OQ}}}{v}\bigg) \\ \quad\quad\quad\quad = A\sin 2\pi \, f \,\bigg(t -\bun{\overline{\mathrm{OQ}}}{v} \bigg ) \] ここで図1で薄青,薄黄で着色した二つの三角形部分に着目して線分 $\overline{\mathrm{OQ}}$ を $x$ , $y$ を使って表すと,\[\overline{\mathrm{OQ}}=x\cos\theta + y\sin\theta \\ \therefore \phi(x, \, y,\, t)= A\sin 2\pi \, f \,\bigg(t -\bun{\overline{\mathrm{OQ}}}{v} \bigg ) \\ \quad\quad\quad\quad = \color{red}{A\sin 2\pi \, f \,\bigg(t -\bun{x\cos\theta + y\sin\theta}{v} \bigg ) } \cdots\cdots\maru{4} \\ \quad\quad\quad\quad = A\sin 2\pi \, f \,\bigg\{t -\bigg( \bun{x}{\bun{v}{\cos\theta}} + \bun{y}{\bun{v}{\sin\theta}} \bigg ) \bigg\} \\ \quad\quad\quad\quad = \color{red}{A\sin 2\pi \, f \,\bigg\{t -\bigg( \bun{x}{w_x} + \bun{y}{w_y} \bigg ) \bigg\} } \cdots\cdots\maru{5}\] $\maru{4}$ 式,もしくは$\maru{5}$ 式が, $x$ 軸に対して角 $\theta$ の方向に進む平面波の一般式ということになる。
【参考】波数ベクトルを使った平面波の式
$\maru{4}$ 式より, \[ \phi(x, \, y,\, t)= A\sin 2\pi \, f \,\bigg(t -\bun{x\cos\theta + y\sin\theta}{v} \bigg ) \\ \quad\quad\quad\quad = A\sin \,\bigg( 2\pi f t - 2\pi \bun{x\cos\theta + y\sin\theta}{v / f} \bigg )\\ \quad\quad\quad\quad = A\sin \,\bigg( \omega \, t - 2\pi \bun{x\cos\theta + y\sin\theta}{\lambda} \bigg ) \\ \quad\quad\quad\quad = A\sin \,\bigg\{ \omega \, t - \bun{2\pi}{\lambda} \bigg( x \cdot\cos\theta + y \cdot\sin\theta\bigg )\bigg\} \\ \quad\quad\quad\quad = A\sin \,\bigg\{ \omega \, t - \bigg(\bun{2\pi}{\lambda}\cos\theta \cdot x + \bun{2\pi}{\lambda}\sin\theta \cdot y \bigg )\bigg\} \] ただし,$2\pi f = \omega $ , $\bun{v}{f} = \lambda$ とおいた。$\omega$ は 角振動数, $\lambda$ は波長である。
ここで,大きさが $\boldsymbol{\bun{2\pi}{\lambda}}$ で,波面に垂直で波面の進行方向に向くベクトル $\Vec{k}$ ( 波数ベクトル と呼ばれる)を定義すると,その $x$ 成分 $k_x$ , $y$ 成分 $k_y$ は, \[\quad |\Vec{k}| = \bun{2\pi}{\lambda} \\ \therefore k_x = |\Vec{k}|\cos\theta = \bun{2\pi}{\lambda}\cos\theta \\ \quad k_y = |\Vec{k}|\sin\theta= \bun{2\pi}{\lambda}\sin\theta \] であるから(下図参照),上式は, \[\phi(x, \, y,\, t) = A\sin \,\bigg\{ \omega \, t - \bigg(\bun{2\pi}{\lambda}\cos\theta \cdot x + \bun{2\pi}{\lambda}\sin\theta \cdot y \bigg )\bigg\} \\ \quad\quad\quad\quad = A\sin \,\bigg\{ \omega \, t - \bigg(k_x\cdot x + k_y\cdot y \bigg) \bigg\} \\ \quad\quad\quad\quad = A\sin \,\bigg( \omega \, t - \Vec{k}\cdot \Vec{r} \bigg) \] のように書き表される。ここで,$ \Vec{k}\cdot \Vec{r}$ は,2つのベクトル $ \Vec{k} (k_x,\,k_y)$ と $ \Vec{r}(x,\,y)$ の内積(スカラー積)で,2つのベクトルの各成分ごとの積の和に等しい。
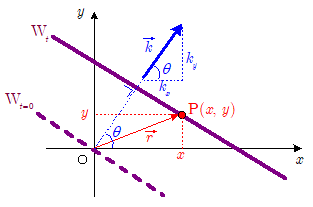
ところで,波数ベクトルとは,具体的にどのような意味をもつの物理量なのであろうか。
まず,波数ベクトルは,平面波の進行方向・向きを表すベクトルであるということが第1点。
またその大きさは $|\Vec{k}| = \bun{2\pi}{\lambda}$ と定義されているが,正弦波では1波長 $\lambda$ ごとに位相が $2\pi$ ずつ変化するので, $\bun{2\pi}{\lambda}$ は単位距離(例えば1〔m〕)あたりの位相の変化量を表す量にほかならない。
つまり波数ベクトルとは,波面の進行方向に沿って単位距離だけ位置を変えたときの波面位相の変化量,すなわち位相の距離変化率を表す物理量…ということが言える。
同様に角振動数 $\omega = 2\pi f = \bun{2\pi}{T}$ ( $T$ :周期) は,単位時間(例えば1〔s〕)だけ時間が経ったときの位相の変化量を表す物理量,すなわち位相の時間変化率と考えることができる。
なお,波の位相速度 $v$ は波数ベクトルと角振動数を使って表され,\[\bun{\omega}{\bigg |\Vec{k}\bigg |} = \bun{2\pi\,f }{ 2\pi/\lambda} = f\,\lambda = v \] となる。
3次元空間を伝わる平面波の場合:
以上の説明を3次元媒質を伝わる平面波に拡張すれば,波数ベクトル $\Vec{k}(k_x, \, k_y, \, k_z)$ と位置ベクトル $ \Vec{r}(x, \, y, \, z)$ を使って,時刻 $t$ における平面波は,一般に,\[\waku{$\phi(x, \, y, \, z,\, t)= A\sin \,\bigg( \omega \, t - \Vec{k}\cdot \Vec{r} \bigg) \\ \quad\quad\quad\quad = A\sin \,\bigg\{ \omega \, t - \bigg(k_x \cdot x + k_y \cdot y + k_z \cdot z \bigg)\bigg\} $} \] なる式で記述されることになる。なお下右図のように,波数ベクトル $\Vec{k}$ が $x$ 軸, $y$ 軸, $z$ 軸とそれぞれ角 $\alpha$ , $\beta$ , $\gamma$ をなすとき, $\Vec{k}$ の各成分は,\[k_x = |\Vec{k}|\cos\alpha = \bun{2\pi}{\lambda}\cos\alpha \\ k_y = |\Vec{k}|\cos\beta = \bun{2\pi}{\lambda}\cos\beta \\ k_z = |\Vec{k}|\cos\gamma = \bun{2\pi}{\lambda}\cos\gamma \] である。
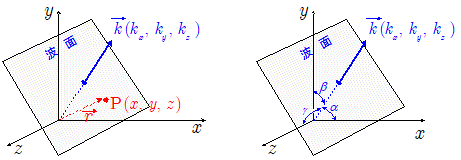
次に続く(平面波の力学モデル) 戻る