空気抵抗のように,物体は運動することによって抵抗力を受けます。ばね振り子にこのような速度に基づく力が作用した場合,どのような運動になるかを考えてみましょう。
水平な床面上で運動するばね振り子に,物体の速度に比例する抵抗力がはたらくものとします。物体の質量を $m$ ,ばねのばね定数を $k$ ,抵抗力の比例定数を $c\,(\,>\,0\,)$ とすると,運動方程式は,
\[m \,\ddif{x}{t} = -k \, x - c\, \dif{x}{t} \\ \kern-1em \therefore m \,\ddif{x}{t} + c\, \dif{x}{t} + k \, x = 0 \quad \cdots\cdots\maru{1} \]
上記 $\maru{1}$ 式で表される微分方程式の一般解は,
(i) $c^2 \ne 4m \, k$ の場合は,\[\kern-1em \left \{ \begin{array}{rl}
& \kern-1em \mu_1 = \bun{1}{2m}(c + \kon{c^2 - 4m\,k}) \\
& \kern-1em \mu_2 = \bun{1}{2m}(c - \kon{c^2 - 4m\,k})
\end{array}\quad \right . \quad \cdots\cdots\maru{2} \]なる $\mu_1$ , $\mu_2$ ,および積分定数 $A$ , $B$ (一般には $A$ , $B$ は複素数)を用いて,\[x = A\,e^{-\mu_1\,t} + B\,e^{-\mu_2\,t} \quad \cdots\cdots\maru{3} \]と表されます。
このとき, $\mu_1$ , $\mu_2$ が複素数になるか実数になるかによって,運動の形が違ってきます。さらに,
(ii)$c^2 = 4m \, k$ の場合は,上記とは別の形の解になり,上の2ケースとは別に考えていく必要があります。
以上3つのケースについて,順次説明していきます。
◎ $c^2 < 4m \, k$ の場合 ・・・・ 減衰振動
これは,抵抗力が比較的小さい場合に相当します。
このときは $\maru{2}$ 式の根号内が負になるので, $\kon{c^2 - 4m\,k}$ は虚数になります。ここで\[ \kern-1em \left \{ \begin{array}{rl}
& \kern-1em \mu = \bun{c}{2m} \\
& \kern-1em \omega_0 = \kon{\bun{k}{m}} \\
& \kern-1em \omega = \bun{\kon{4m\,k - c^2}}{2m} = \kon{\omega_0{}^2 - \mu^2 }
\end{array} \right . \]とおくと, $\maru{2}$ 式の $\mu_1$ , $\mu_2$ は,$i$ を虚数単位として,
\[\kern-1em \left \{ \begin{array}{rl}
& \kern-1em \mu_1 = \bun{1}{2m}(c + \kon{c^2 - 4m\,k}) \\
& \kern-1em \quad = \mu + i\,\omega \\
& \kern-1em \mu_2 = \bun{1}{2m}(c - \kon{c^2 - 4m\,k}) \\
& \kern-1em \quad = \mu - i\,\omega \\
\end{array}\quad \right . \]となるので,一般解 $\maru{3}$ 式は,\[x = A\,e^{-\mu_1\,t} + B\,e^{-\mu_2\,t} \\ \kern0.5em = A\,e^{-(\mu\, + \, i\, \omega)t} + B\,e^{-(\mu\, - \, i\, \omega)t} \\ \kern0.5em = e^{-\mu\, t}(A\,e^{- i\, \omega\,t} + B\,e^{ i\, \omega\,t} ) \]
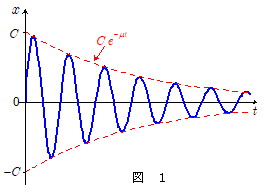
ここで指数関数と三角関数との関係(オイラーの公式)を利用し,さらにその実数部分をとった上で三角関数の合成の式を使うと,上式は\[\bbold{ x = C\cdot e^{-\mu\, t}\cdot \cos(\omega \, t + \phi) } \quad \cdots\cdots\maru{4} \]のようになります。 $C$ , $\phi$ は任意の定数で,初期条件で決まります。
下図はその一例です。このときの角振動数 $\omega$ は \[\omega = \kon{\omega_0{}^2 - \mu^2} \\ \kern-1em\therefore \omega < \omega_0 \]なので,抵抗力が作用しないときの角振動数 $\omega_0 = \kon{\bun{k}{m}}$ より小さくなります(周期は伸びる)。また,振幅は指数関数的に減少していきます。
このような振動を減衰振動と言います。
◎ $c^2 > 4m \, k$ の場合 ・・・・ 過減衰
これは,抵抗力が比較的大きい場合に相当します。
このときは $\maru{2}$ 式の根号内は正なので, $\mu_1$ , $\mu_2$ は実数です。よって, \[ \kern-1em \left \{ \begin{array}{rl} & \kern-1em \mu = \bun{c}{2m} \\ & \kern-1em \omega_0 = \kon{\bun{k}{m}} \\ & \kern-1em \sigma = \bun{\kon{ c^2 - 4m\,k}}{2m} = \kon{\mu^2 -\omega_0{}^2 } \end{array} \right . \]とおくと,$\maru{2}$ 式は, \[\kern-1em \left \{ \begin{array}{rl} & \kern-1em \mu_1 = \bun{1}{2m}(c + \kon{c^2 - 4m\,k}) \\ & \kern-1em \quad = \mu + \sigma \\ & \kern-1em \mu_2 = \bun{1}{2m}(c - \kon{c^2 - 4m\,k}) \\ & \kern-1em \quad = \mu - \sigma \\ \end{array}\quad \right . \] よって $\maru{3}$ 式の一般解 $x$ は,\[\bbold{x = e^{- \,\mu\,t}(A\,e^{-\sigma\,t} + B\,e^{\sigma\,t} ) } \quad\cdots\cdots\maru{5}\] この場合は振動は起きず(非周期運動),時間とともに単調に減衰していく場合と,高々一度だけ極値をとる場合とがあります(下図参照)。これを過減衰な状態と言います。
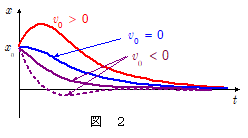
上図は,初期位置 $x_0 \,>\,0$ から出発した場合の変位 $x$ の時間変化を表しています。このとき4つの変化のパターンがあります。
初速度 $v_0\,>\,0$ もしくは $v_0 = 0$ であれば,常に $x\,>\,0$ の状態で $0$ に漸近していきます(図の赤線,青線)。
$v_0 \,< \,0$ の場合(紫)は,常に $x\,>\,0$ の場合(紫の実線)と, 負の極小値を経た後に $0$ に漸近していく場合とがあります(紫の破線)。破線のような変化をするのは, $|v_0|$ と $x_0$ の間に \[|v_0| \,>\, \mu_1\, x_0\] の関係がある場合です。
本シミュレーションでは,台に固定された原点Oからの変位 $x$ を『ばねの伸び』として表示していますが,紫の破線のような変化はグラフ表示では確認しづらいかもしれません。この場合は,『ばねの伸び』の数値変化を読み取ることで確認できます。このためには「描画スピード」をなるべく遅くすると良いでしょう。これによって,『ばねの伸び』が 正の値→負の値→負の極値→ $0$ に漸近 という一連の変化が確認できるようになります。
質量 $m = 1.0$ , ばね定数 $k = 1.0$ とすると,$c^2 > 4m \, k$ であるためには\[抵抗係数 c > \kon{4m\,k} = 2.0 \] よって,抵抗係数 $c = 2.5$ とすると,\[ \mu_1 = \bun{1}{2m}(c + \kon{c^2 - 4m\,k}) = 2.0\]よって初速 $v_0 = -200$ とするなら,\[初期位置 \quad x_0 < \bun{|v_0|}{\mu_1} = 100 \]上式を満たす $x_0$ を選んで試してみてください。(あまりギリギリの値を選ぶと,本シミュレーションの精度では期待通りの結果が出ない可能性もあります。)
◎ $c^2 = 4m \, k$ の場合 ・・・・ 臨界減衰
この場合は先の $\maru{2}$ 式の $\mu_1$ , $\mu_2$ における根号内が $0$ になるので, $x$ の一般解は, \[\mu = \bun{c}{2m} \]なる $\mu$ を用いて,\[\bbold{x = (A\,t + B )\cdot e^{-\,\mu\,t}} \quad\cdots\cdots\maru{6} \]のようになります。 $A$ , $B$ は定数で,初期条件で決まります。臨界減衰,限界制動などと呼ばれます。
この場合も振動は起きず,非周期運動となります。$c^2 \, >\,4m \, k$ の場合と同様に, $x$ の時間変化には4つのパターンがあり,図2と同様なグラフになります。 $v_0\,>\,0$ もしくは $v_0 = 0$ であれば常に $x\,>\,0$ の状態で $0$ に漸近, $v_0 \,< \,0$ であれば,常に $x\,>\,0$ か, 負の極小値を経た後に $0$ に漸近,の2通りになります。
紫色破線のように負の極小値を経る場合の条件は,\[|v_0| \,>\, \mu\,x_0 \]の関係がある場合です。
質量 $m = 1.0$ , ばね定数 $k = 1.0$ とすると,$c^2 = 4m \, k$ であるためには\[抵抗係数 c = \kon{4m\,k} = 2.0 \\ \kern-1em \therefore \mu = \bun{c}{2m} = 1.0 \] よって初速 $v_0 = -100$ とするなら,\[ 初期位置 \quad x_0 < \bun{|v_0|}{\mu} = 100 \] 上式を満たす $x_0$ を選んで試してみてください。。
ただし,あまりギリギリの値を選ぶと,本シミュレーションの精度では期待通りの結果が出力されなくなりますのでご注意ください。
たとえば $v_0 = -100$ , $x_0 = 90$ の場合を数学ソフトMathematica で計算すると, $x$ は時刻 $t = 10$ で負の極小値 $x = -0.000454$ となり,この場合は本シミュレーションでの『ばねの伸び』の数値変化で検証できました。しかし $v_0 = -100$ , $x_0 = 95$ の場合では検証できませんでした。
◎ 抵抗力を受ける場合のまとめ
物体にはたらく抵抗力は,物体の運動を妨げようとする『ブレーキ』の役割を持ちます。その『ブレーキ』効果は,抵抗力の比例定数の大小,および物体の速度の大小にかかわってきます。
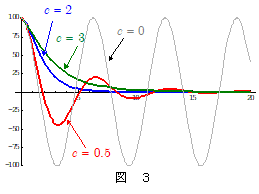
下の図3のグラフは,抵抗力の大きさ,つまり抵抗力の比例定数 $c$ の違いによって物体の運動にどのような違いが生じるかを示したものです。
設定値は,物体の質量 $m = 1$ ,ばね定数 $k = 1$ , $\therefore \omega_0 = \kon{\bun{k}{m}} = 1$ ,初期位置 $x_0 = 100$ ,初速度 $v_0 = 0$ になっています。
(a) グレー線: $c = 0$ の場合 → 抵抗力,無し → 減衰することなく振動が続く。
(b) 赤の線: $c = 0.5\quad \therefore c^2 < 4m\,k$ → 抵抗力が弱い場合 → 減衰振動 → 振動しながら減衰。
(c) 青の線: $c = 2\quad \therefore c^2 = 4m\,k$ の場合 → 臨界制動 → 減衰の仕方が最も著しい。
(d) 緑の線: $c = 3\quad \therefore c^2 > 4m\,k$ の場合 → 抵抗力が強い → 過減衰 → 振動しないで減衰。
抵抗力の大きさが物体の速度(の大きさ)に比例する場合,物体の速度が大きいほど抵抗力は大きく,物体の速度は急速に落ちてきます。物体の速度は図3のような $x - t $ グラフにおいて,その接線の傾きに等しくなります。『過減衰』の場合も『臨界制動』の場合も,グラフの傾きが時間経過とともに緩くなってきているのは,速度が徐々に落ちてきていることを意味します。速度が小さくなれば逆に『ブレーキ』効果が弱くなり,速度の変化量(グラフの傾きの変化量)も小さくなってきます。そのために $x - t $ グラフは $t$ 軸に接するように漸近してくことになります。
一方, $c = 2$ の場合よりも $c = 3$ の場合の方がゆっくりと減衰していくのは, $c $ が大きいほど『ブレーキ』効果が大きく,ばねの復元力によって物体が引き戻されていく速度がなかな増大せず,そのためにゆっくりと移動することになるのです。
強制振動 に続く。