水平な床面上で運動するばね振り子に摩擦力がはたらくと,どのような運動になるかを考えてみます。
ばね定数 $k$ のばねに結ばれた物体の質量を $m$ ,動摩擦力の大きさを $f$ ,最大静止摩擦力の大きさを $F$ とします。
◎物体が振動を続ける条件
まず,物体が静止の状態から動き出すためには,最大静止摩擦力以上の大きさの力をばねから受けなければなりません。よってばねの自然長からの伸びまたは縮みが $D$ 以上になったとき物体が床面をすべり出すとすれば,このとき\[k\,D = F \\ \kern-2em \therefore \color{red}{伸びまたは縮み \ge D = \bun{F}{k}} \quad \cdots\cdots \maru{1}\]
これが物体が静止の状態から床上をすべり出す条件です。
振動していた物体が振動の折り返し点に達した瞬間,物体の速度は一瞬 $0$ (ゼロ)となって床に静止することになるので,その後物体が再び引き返し始めて振動を続けるかどうかは,そのときのばねの伸びまたは縮みの量が上記 $\maru{1}$ 式を満たしているかどうかで決まってきます。もし折り返し点での伸びまたは縮みの量が $\maru{1}$ 式を満たしていないとすれば物体は再度動き出すことはできず,そのまま床上で静止したままとなり,運動は完全に停止してしまいます。
◎動摩擦力による振動中心のずれ
運動物体にはたらく動摩擦力は,常に物体の運動方向とは逆向きです。
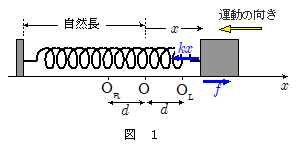
たとえば上図において,物体が $x$ 軸の負方向に運動中であれば,動摩擦力は $x$ 軸正の向きに作用するので,その運動方程式は,\[m \ddif{x}{t} = -k\,x + f \\ \kern 3em = -k\bigg( x - \bun{f}{k}\bigg) \] よって一定力を受けた単振動の項で見たように,物体の運動は単振動となりますが,その振動中心は合力が $0$ となる位置ですので,上式の右辺を $0$ とおいて,\[x = +\bun{f}{k} \quad (= + d \,) \] なる点 $\mathrm{O_L}$ を中心とした単振動となります。その周期 $T = 2\pi\kon{\bun{m}{k}}$ ですが,この運動は動摩擦力の向きが変わらない間,つまり物体の運動の向きが反転するまでしか続きません。したがって,初速 $0$ で $x$ 軸の負方向に動き出した物体であれば, $\mathrm{O_L}$ を中心とした単振動を折返し点に達するまでの間,つまり半周期分だけ続けることになります。
折り返し点に達した物体はその後運動の向きを反転し,$x$ 軸の正方向に運動を開始します。このとき動摩擦力は $x$ 軸負の向きに作用するので,その運動方程式は,\[m \ddif{x}{t} = -k\,x - f \\ \kern 3em = -k\bigg( x + \bun{f}{k}\bigg) \] となります。よって物体の運動は \[x = -\bun{f}{k} \quad (= - d \,) \] なる点 $\mathrm{O_R}$ を中心とした周期 $T = 2\pi\kon{\bun{m}{k}}$ の単振動を始めますが,上記と同様,半周期後には反対側の折り返し点に達して一瞬停止します。さらにその後,再び $x$ 軸の負方向に戻っていくので, $\mathrm{O_L}$ を中心とした単振動を半周期分続ける……ということが繰り返されます。
このように,物体は半周期ごとに運動の向きを変え,そのたびに振動中心が,$\mathrm{O_L}$ → $\mathrm{O_R}$ → $\mathrm{O_L}$ → $\mathrm{O_R}$ →……と入れ替わっていくことになります。
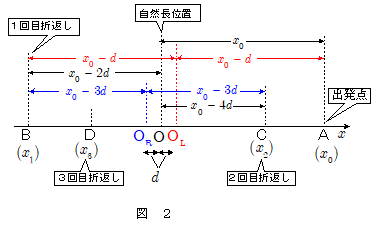
たとえば図2のように,ばねの自然長の位置を原点Oとして, $x = x_0 > 0$ なる点Aから物体が滑り出したとします。このときの振動中心は $\mathrm{O_L}$ ですから, $d = \bun{f}{k}$ として,その振幅は $\overline{\mathrm{AO_L}} $ 間の距離,すなわち $x_0 - d$ となります。この運動を半周期分続けると物体は折返し点Bに達し,一瞬停止します。その距離は振動中心 $\mathrm{O_L}$ から測って $x_0 - d$ なので,自然長位置(原点)Oからの距離はさらに $\overline{\mathrm{O_LO}} = d $ だけ差し引いて $x_0 - 2d$ となります。したがって点Bの $x$ 座標は $x_1 = -(x_0 - 2d)$ となります。
ここで物体が引き返し始めたとすると,今度は振動中心が $\mathrm{O_R}$ になるので,振幅はさらに $\overline{\mathrm{O_RO}} = d$ だけ短くなり, $x_0 - 3d$ となります。したがって2回目の折り返し点Cの $x$ 座標は $x_2 = (x_0 - 4d)$ となります。
以後,折り返し点の$x$ 座標は, $x_3 = - (x_0 - 6d)$ ,$x_4 = (x_0 - 8d)$ , $\cdots\cdots\cdots$ と,折り返し点におけるばねの伸縮量が前述した $\maru{1}$ 式を満たさなくなるまで続くことになります。
以上より,摩擦力を受けたばね振り子の運動は,
◎ばねの自然長の位置を1回通過するごとにばねの最大伸縮量は $2d = \bun{2f}{k}$ ずつ減少していく。
◎折返し点~折返し点の所要時間は 半周期 $\bun{T}{2} = \pi\kon{\bun{m}{k}}$ である。
◎折り返し点での伸縮量が $D = \bun{F}{k}$ 以下になると運動は完全停止する。
のようにまとめられます。
下図は,摩擦力を受けながら振動するばね振り子の変位 $x$ の時間変化の一例です。折返し点でのばねの伸縮量は $2d = \bun{2f}{k}$ ずつ減少していきます。そして折返し点が図のグレーゾーン内( $2D = \bun{2F}{k}$ ) に入ってしまうと,物体は完全に停止してしまいます。
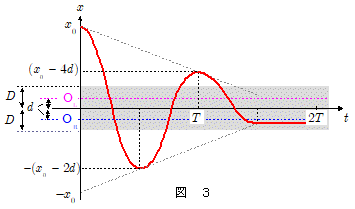
減衰振動-抵抗力を受けるばね振り子 に続く。