１．曲面(ベジェ曲面)はどうやって作る？
　--- ベジェ曲面を作るための数学の知識とプログラミング方法を学びます。---

　　B)級数(数列の和)ってどう使う。そして曲面へ

　　● 制御点が３点と４点の時の計算式を作ってみる。
　　　前回1.A)では、図を使って曲線(ベジェ曲線)上の点を求めてみました。しかしコンピュータでは図からではなく計算式から、
　　　求めなくてはなりません。今回1.B)では、その計算式を、図を基に作って見ます。
　　　その前に、次の事柄を頭に入れておいてください。
　　　　1.　各点は、x、y、z座標からなっています、従って求めた式からx、y、z座標を求めるためには、同じ式を使ってそれ
　　　　　　ぞれの座標を求めます。
　　　　2.　内分比から点を求める方法は次のようになります。
　　　　　　P(u) = Q₀(1.0 - u) + Q₁u
　　　　　　例）始点Q₀が３で、終点Q₁が５で、uが0.4(10等分の4等分目)の値を求める
　　　　　　┣━━╋━━╋━━╋━━╋━━╋━━╋━━╋━━╋━━╋━━┫
　　　　　Q₀=３←────────→P(u)←──────────────→Q₁=５
　　　　　　┗━━━━━━━━━━━┻━━━━━━━━━━━━━━━━━┛
　　　　　　　　u = 4/10 = 0.4←────────→( 1.0 - u ) = 0.6

　　　　　　P(u) = Q₀(1.0 - u) + Q₁u = 3 X 0.6 + 5 X 0.4 = 3.8となります。
　　　　　　※小学校高学年レベルの算数なので思い出しておいてください。

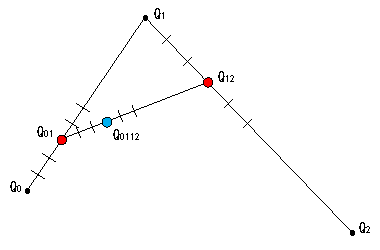
　　　　それでは、制御点が３点の場合の曲線上の点を求める一般式を求めてみましょう。

　　　　Q₀₁₁₂を求める。
　　　　　内分比を使って求めると、次のようになります。
　　　　　Q₀₁₁₂ = Q₀₁(1.0 - u) + Q₁₂u -----(1)
　　　　　Q₀₁ = Q₀(1.0 - u) + Q₁u -----(2)
　　　　　Q₁₂ = Q₁(1.0 - u) + Q₂u -----(3)
　　　　　(2)と(3)を(1)へ代入すると次のようになります。

　　　　　Q₀₁₁₂ = (Q₀(1.0 - u) + Q₁u)(1.0 - u) + (Q₁(1.0 - u) + Q₂u )u
　　　　　これを展開すると
　　　　　Q₀₁₁₂ =
　　　　　整理すると次のようになります。
　　　　　P(u) = Q₀₁₁₂ =
　　　　　Pは、u が変化する度に求まる点なので、u はPのパラメータと呼ばれます。(※ u は内分比なので、0.0≦ u ≦1.0)

　　　　次に、制御点が４点の場合の曲線上の点を求める一般式を求めてみましょう。

　　　　Q_01121223を求める。
　　　　　内分比を使って求めると、次のようになります。
　　　　　Q_01121223 = Q₀₁₁₂(1.0 - u) + Q₁₂₂₃u --------------------(1)
　　　　　Q₀₁₁₂ = Q₀₁(1.0 - u) + Q₁₂u --------------------(2)
　　　　　Q₁₂₂₃ = Q₁₂(1.0 - u) + Q₂₃u --------------------(3)
　　　　　Q₀₁ = Q₀(1.0 - u) + Q₁u --------------------(4)
　　　　　Q₁₂ = Q₁(1.0 - u) + Q₂u --------------------(5)
　　　　　Q₂₃ = Q₂(1.0 - u) + Q₃u --------------------(6)
　　　　　(4)と(5)と(6)を(2)と(3)へ代入すると次のようになります。
　　　　　Q₀₁₁₂ = (Q₀(1.0 - u) + Q₁u)(1.0 - u) + (Q₁(1.0 - u) + Q₂u)u
　　　　　　　　　= --------------------(2')
　　　　　Q₁₂₂₃ = (Q₁(1.0 - u) + Q₂u)(1.0 - u) + (Q₂(1.0 - u) + Q₃u)u
　　　　　　　　　= --------------------(3')
　　　　　さらに(2')と(3')を(1)へ代入すると次のようになります。

　　　　　Q_01121223 =
　　　　　これを展開すると
　　　　　Q_01121223 =
　　　　　整理すると次のようになります。
　　　　　P(u) = Q_01121223 =
　　　　　Pは、u が変化する度に求まる点なので、u はPのパラメータと呼ばれます。(※ u は内分比なので、0.0≦ u ≦1.0)

　　　これで、制御点が３点の場合と、制御点が４点の場合の一般式が出来上がりました。

　　● 曲線(ベジェ曲線)の一般式を作ってみる。
　　　次に、制御点が何点の場合でも対応できる、さらなる一般式を求めてみたいと思います。

　　　　制御点が３点の場合の式：P(u) = --------------------(7)
　　　　制御点が４点の場合の式： P(u) = --------------------(8)
　　　　を次のように書き換えてみます。
　　　　制御点が３点の場合の式：P(u) = --------------------(9)
　　　　制御点が４点の場合の式：P(u) = --------------------(10)
　　　　ここで u の０乗は１です、ちなみにどのような値も０乗すると１になります。
　　　　通常１のかけ算では１は書かないので、(9)と(7)、(10)と(8)は同じ式です。

　　　　ここで(10)式を見てみましょう。
　　　　 P(u) =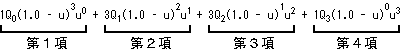

　　　　各項は、内分比に対する制御点の混合割合の値を示しています。
　　　　ここで各項の係数は見てみましょう。

　　　　 (9)と(10)の式の係数を並べて書いてみます、さらに制御点が５点の場合も書いてみると下記のようになります。
　　　　

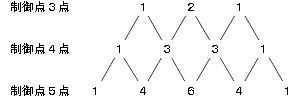
　　　　これは有名なパスカルの三角形と言われる物で、高校１年のときにお目にかかった人も多いのではと思います。
　　　　このパスカルの三角形には多くの数列が含まれています、また最短経路問題とも関連しています。
　　　　パスカルの三角形は、二項展開における係数を三角形状に並べた物です。この係数を二項係数といいます。
　　　　

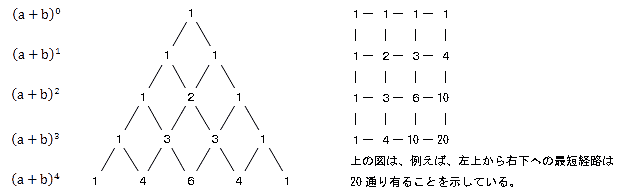
　　　　この二項係数は、次式により求められます。

　　　　c( n, i ) = _nC_i = 　　　　　※ただし、n! = n・(n - 1)・(n - 2)．．．3・２・1 (nの階乗)
　　　　例) 3! = 3・2・1 = 6 で、また 0! = 1であり、1! = 1 です。

　　　　制御点が４点(n = 3)の場合は、 i = 0で第1項の係数, i = 1で第2項の係数, i = 2で第3項の係数, i = 3で第4項の係数です。
　　　　したがって、(10)式を一般式で書くと次式になります。
　　　　P(u) = -------------------(11)
　　　　※ただし、0.0 ≦ u ≦ 1.0

　　　● 級数(数列の和)について
　　　　これは数列の和で、この場合には i が変わる度に加算して行く事を意味しています。
　　　　　例）
　　　　　　S =
　　　　　　上記の式は、 S = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 と同じ意味です。

　　　　制御点が４点( n = 3 )の場合には、i = 0 のとき第１項、i = 1 のとき第２項、i = 2 のとき第３項、i = 3 のとき第４項、

　　　　となり、加算すると 内分比 u に対する曲線(ベジェ曲線)上の点が求まる事になります。

　　　● そして、曲面へ
　　　　これを平面に拡張すると、ベジェ曲面になり、次式で表します。
　　　　

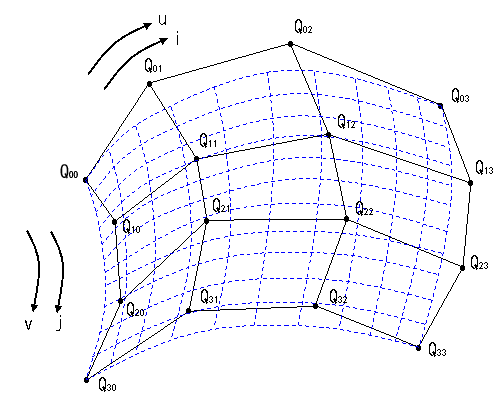
　　　　S(u, v) = --------------------(12)
　　　　※ただし、0.0 ≦ u, v ≦ 1.0
　　　　(12)式は、一般に次のように表現されています。
　　　　S(u, v) =
　　　　B_jm(v) = C( j, m )・( 1.0 - v )^m-j・v^j
　　　　B_in(u) = C( i, n )・( 1.0 - u )^n-i・uⁱ
　　　　これは、バーンスタインの基底関数と呼ばれるもので、B はその頭文字です。またS(u, v)の S は Surface(表面)の
　　　　頭文字です。

　　　　次回は、曲線(ベジェ曲線)上の点の座標値を求める(11)式を、 C言語プログラミングでは、どのように記述するかに
　　　　ついてです。( 再帰呼び出し、関数 )

目次 1.A) 1.B)

このページは正当なCSSです。