$\bbold{1}$. Pが上昇中であれば, Pの最高点 $Y_{\mathrm{P},max} = $P・Qの衝突点の高さ $Y$ となり(下図の青色の放物線(b)),
$\bbold{2}$. 落下中ならば, Pの最高点 $Y_{\mathrm{P},max} = $Pの放物運動における最高点 $y_{\mathrm{P},max}$ となる(下図の紫色の放物線(c))。
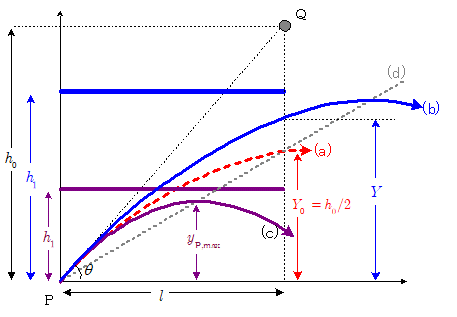
ここで,衝突時刻 $t=t_0$ におけるPの鉛直方向の速度成分 $v_{\mathrm{P},y}$ は$\Maru{10}$ 式より,衝突点の高さ $Y$ は $\maru{8}$ 式より,それぞれ,\[v_{\mathrm{P},y} = v_0\bun{h_0}{\kon{l{}^2 + h_0{}^2}} - g\bun{\kon{l{}^2 + h_0{}^2}}{v_0} \cdots\cdots\Maru{10} \\ Y = h_0 - \bun{1}{2}g \bigg(\bun{\kon{l{}^2 + h_0{}^2}}{v_0} \bigg)^2 \cdots\cdots\maru{8} \] そして $v_0=w_0$ の時, \[v_{\mathrm{P},y} = 0 \\ Y = Y_0 = \bun{h_0}{2} \] であった。よって, \[ \left \{ \begin{array}{rl} & \kern-1em v_0 > w_0 なら v_{\mathrm{P},y} > 0 \rightarrow 上昇中で, Y > \bun{h_0}{2} \\ & \kern-1em v_0 < w_0 なら v_{\mathrm{P},y} < 0 \rightarrow 落下中で, Y < \bun{h_0}{2} \end{array} \right . \] よって ,Pが天井に衝突しない条件は,
$\bbold{1}$. $h_1 \ge \bun{h_0}{2}$ なら,\[h_1 > 衝突点の高さ Y= h_0 - \bun{1}{2}g \bigg(\bun{\kon{l{}^2 + h_0{}^2}}{v_0} \bigg)^2 \\ \therefore v_0 < \kon{\bun{g(l^2 + h_0{}^2)}{2(h_0 - h_1)}}\] 空中で衝突する条件 $\maru{9}$ 式と合わせて, \[ \kon{\bun{g(l{}^2 + h_0{}^2)}{2h_0}} \le v_0 < \kon{\bun{g(l^2 + h_0{}^2)}{2(h_0 - h_1)}} \] $\bbold{2}$. $h_1 < \bun{h_0}{2}$ なら, \[h_1 > Pの放物運動の最高点 y_{\mathrm{P},max} \\ \quad = \bun{(v_0\sin\theta)^2}{2g} \\ \quad = \bun{v_0{}^2}{2g}\bigg(\bun{h_0}{\kon{l^2 +h_0{}^2}} \bigg)^2 \\ \therefore v_0 < \kon{\bun{2gh_1(l^2 + h_0{}^2)}{h_0{}^2}} \] 空中で衝突する条件 $\maru{9}$ 式と合わせて, \[ \kon{\bun{g(l{}^2 + h_0{}^2)}{2h_0}} \le v_0 < \kon{\bun{2gh_1(l^2 + h_0{}^2)}{h_0{}^2}} \] なお,上記の範囲内にある $v_0$ が存在するためには,以下の条件が必要である。\[\kon{\bun{g(l{}^2 + h_0{}^2)}{2h_0}} < \kon{\bun{2gh_1(l^2 + h_0{}^2)}{h_0{}^2}} \\ \therefore h_1 > \bun{h_0}{4}\] 以上をまとめると,Pが天井にぶつかることなく,かつ空中でQと衝突する $v_0$ の条件は,\[ ◎ \bun{h_0}{2} \le h_1 なら, \\ \quad\quad \underline{\kon{\bun{g(l{}^2 + h_0{}^2)}{2h_0}} \le v_0 < \kon{\bun{g(l^2 + h_0{}^2)}{2(h_0 - h_1)}}} \\ ◎ \bun{h_0}{4} < h_1 < \bun{h_0}{2} なら, \\ \quad\quad \underline{\kon{\bun{g(l{}^2 + h_0{}^2)}{2h_0}} \le v_0 < \kon{\bun{2gh_1(l^2 + h_0{}^2)}{h_0{}^2}} } \\ ◎ h_1 \le \bun{h_0}{4} なら, \underline{条件を満たす v_0 は存在しない。} \] (すなわち,Pは,天井にぶつかるか,さもなくばQに衝突する前に地面に落下してしまう,のいずれか。)
【参考】Pの放物運動における最高点の $x$ 座標, $y$ 座標 を $x_{\mathrm{P},max}$ 座標, $y_{\mathrm{P},max}$ とすると,\[ \left \{ \begin{array}{rl} & \kern-1em 最高点到達時刻 \, t_m = \bun{v_0\sin\theta}{g} \\ & \kern-1em \therefore x_{\mathrm{P},max} = v_0\cos\theta \,\cdot t_m = \bun{v_0{}^2\sin\theta\cos\theta}{g} \\ & \kern-1em \quad y_{\mathrm{P},max} = \bun{(v_0\sin\theta)^2}{2g} \end{array} \right . \\ \therefore y_{\mathrm{P},max} = \bun{\tan\theta}{2}\cdot x_{\mathrm{P},max} \cdots\cdots\Maru{13} \]となり,発射角 $\theta$ を一定にして初速度 $v_0$ を色々変えた場合,放物運動の最高点は上記 $\Maru{13}$ 式で示される直線に乗る。この直線が,前図の薄い灰色の破線で示した直線(d)である。
戻 る