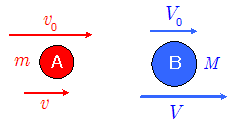
\[ \left\{ \begin{array}{cl} & \kern -1em 運動量保存則: mv+MV=mv_0+MV_0 \\ & \kern -1em はね返り係数: \bun{v-V}{v_0-V_0}=-e \\ \end{array} \right . \quad\cdots\quad\maru{1}\\ \therefore \left\{\begin{array}{ll} & \kern -1em v=\bun{(m-eM)v_0+M(1+e)V_0}{m+M} \\[1em] & \kern -1em V=\bun{m(1+e)v_0+(M-em)V_0}{m+M} \end{array} \right . \quad\cdots\quad\maru{2} \] もし球AとBの質量が等しく($m=M$),弾性衝突($e=1$)であれば,$\maru{2}$式より, \[v=V_0, V=v_0\] となり,衝突によって速度が入れ替わることになる。
◎複数球の1次元多重衝突:
つぎに,本テーマである,直線状に並べられた小球間の多重衝突 を考える。
この衝突が同質量の小球による弾性衝突であるとすれば、上に述べたように,衝突によって次々と速度の交換が起きていく。
簡単な一例として、たとえば下図(1)のように,静止しているB,Cの球に球Aを速度$v_0$で衝突させる場合を考えよう。
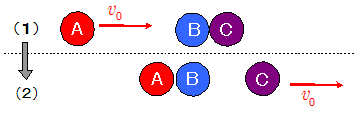
最初の衝突で、まず球AとBの速度交換が起き、球Aが静止し,球Bが速度$v_0$を得る。その直後に球BとCの衝突が起き,速度交換によって球Bが静止し,球Cが速度$v_0$を得る。結果的には上図(2)のように,球AとBが静止し,球Cが速度$v_0$で動いていく。これらの一連の衝突はほとんど瞬時に起きるので,速度が一瞬にして伝わったように見える。
つぎに下図(1)のように,静止している球Cに球Aと球Bを速度$v_0$で衝突させるとどうなるか。
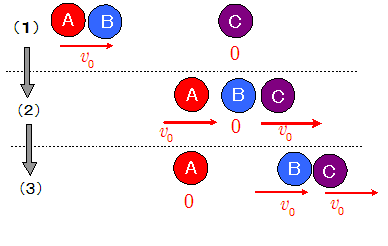
まず最初にBとCの衝突が起き,この2球間の速度交換によってBが静止し,Cが$v_0$を得る(上図(2))。
その直後に,静止したばかりのBにAが衝突してくるので,今度はAとBの速度交換によってAが静止し,Bは$v_0$となる。
この結果上図(3)のように,Aは静止し,BとCが速度$v_0$をもつので,以後3球による衝突は起きない。
以下にその変化を表にしてある。
| 球A | 球B | 球C | |
| (1) | $v_0$ | $v_0$ | $0$ |
| (2) | $v_0$ | $0$ | $v_0$ |
| (3) | $0$ | $v_0$ | $v_0$ |
このようにして衝突が次々と連続して起こるためにあたかも速度が伝わっていくように見えますが,個々の衝突が連続して起きているわけです。本アニメにおいて,球どうしの間隔を空けて試すと,衝突が次々と起きていく様子がよくわかります。
では次に,下図(1)のように,静止ている球B,Cに,その2倍の質量をもつ球Aを$v_0$で弾性衝突したらどうなるだろうか?
Aが止まって,BとCが動き出す…? 残念ながら,そうはなりません。
この問題は,過去に青学大の入試問題として出題されたことがあります。
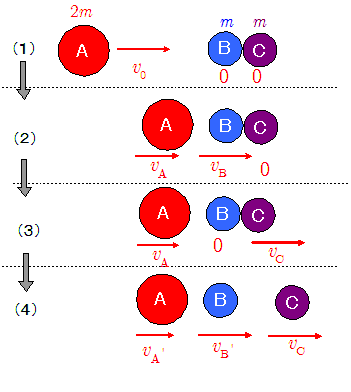
まずAとBの1回目の衝突を考える。衝突直後のA,Bの速度を$v_\mathrm{A}$,$v_\mathrm{B}$とすると,前述の$\maru{2}$式において,$m$にぶつかってくるAの質量として$2m$を,$M$にぶつけられる方のBの質量として$m$を,さらに$e=1$を代入してください。(上図(2)の状態。)
\[ \left\{\begin{array}{ll} & \kern -1em v_\mathrm{A}=\bun{(2m-1\times m)v_0+m(1+1)\times 0}{2m+m} =\bun{1}{3}v_0\\[1em] & \kern -1em v_\mathrm{B}=\bun{2m(1+1)v_0+(m-1\times 2m)\times 0}{2m+m} = \bun{4}{3}v_0 \end{array} \right . \] この直後にBとCの衝突が起き,両者の速度交換が起き(上図(3)),Bの速度は$0$,Cは$v_\mathrm{C}=v_\mathrm{B}=\bun{4}{3}v_0$となる。
さらにその直後に,速度$0$となっているBにAが速度を$v_\mathrm{A}$で2度目の衝突を起こす(上図(4))。衝突直後の速度$v_\mathrm{A}{}'$,$v_\mathrm{B}{}'$は,再び先の$\maru{2}$式を使って, \[ \left\{\begin{array}{ll} & \kern -1em v_\mathrm{A}{}'=\bun{(2m-1\times m)\bun{1}{3}v_0+m(1+1)\times 0}{2m+m} =\bun{1}{9}v_0\\[1em] & \kern -1em v_\mathrm{B}{}'=\bun{2m(1+1)\bun{1}{3}v_0+(m-1\times 2m)\times 0}{2m+m} = \bun{4}{9}v_0 \end{array} \right . \] この結果,$ \bun{1}{9}v_0 < \bun{4}{9}v_0 < \bun{4}{3}v_0$, よって $v_\mathrm{A}{}' < v_\mathrm{B}{}' < v_\mathrm{C}$
の関係となり, 3球はバラバラに離れていくことになり,これ以上の衝突は起きません。よって最終速度は下表のようになる。
| 球A | 球B | 球C | |
| (1) | $v_0$ | $0$ | $0$ |
| (2) | $\bun{1}{3}v_0$ | $\bun{4}{3}v_0$ | $0$ |
| (3) | $\bun{1}{3}v_0$ | $0$ | $\bun{4}{3}v_0$ |
| (4) | $\bun{1}{9}v_0$ | $\bun{4}{9}v_0$ | $\bun{4}{3}v_0$ |
◎2球間衝突のおまけの話:
入試問題で扱われる衝突は,ほとんどが2球の衝突です。そこで,ちょっと追加の話です。
小球数を「2」,弾性衝突($e=1$)とし,「計算方法」を単振動として処理として,第1球と第2球の質量をいろいろ変えて実験してみてください。この場合両球の質量の値に関係なく,2球が偶数回目衝突ごとに同じ速度状態に戻り,両球は初めの出発点の高さに戻ります。
この場合,衝突が常に最下点で起きるようにしなければなりませんので,「計算方法」は必ず『単振動として処理』にしておかなければなりません。
(その理由は,後述。)
【解説】 計算が煩雑になるので,はじめ第2球は静止していたとして,$V_0=0$とする。
1回目の衝突直後の速度$v_1$,$V_1$は,先に記した$\maru{1}$式に$V_0=0$,$e=1$を代入して, \[ \left\{\begin{array}{ll} & \kern -1em mv_1+MV_1=mv_0 \\[1em] & \kern -1em \bun{v_1-V_1}{v_0-0}=-1\quad\therefore v_1-V_1=-v_0 \end{array} \right . \quad\cdots\cdots\maru{3}\\[1em] \therefore \left\{\begin{array}{ll} & \kern -1em v_1=\bun{m-M}{m+M} v_0\\[1em] & \kern -1em V_1=\bun{2m}{m+M} v_0 \end{array} \right .\quad\therefore v_1 \ne V_1 \] よって両球は衝突後異なる速度で跳ね上がり,それぞれ異なる高さに達しますが,単振動の場合,その周期は振幅に関係なく,糸の長さ(と重力加速度)だけで決まるので,両球は同じ時間後(=単振動の半周期後)に再度最下点に戻ってきて,ここで2度目の衝突を起こします。最下点に戻ってきたのですから,その時の速さはそれぞれ1回目の衝突直後の速さと同じになっていますが,向きが逆になって戻ってきます。よって,2度目の衝突直前の速度はそれぞれ
$-v_1=-\bun{m-M}{m+M} v_0$, $-V_1=-\bun{2m}{m+M} v_0$
となります。この速度を使って2度目の衝突について運動量保存とはね返り係数の式を立てます。2度目の衝突直後の速度を$v_2$,$V_2$とし,上の$\maru{3}$式も考慮すると, \[ \left\{\begin{array}{ll} & \kern -1em mv_2+MV_2=m(-v_1)+M(-V_1) =-mv_0 \\[1em] & \kern -1em \bun{v_2-V_2}{-v_1-(-V_1)}=-1 \quad\Rightarrow\quad v_2-V_2=(v_1-V_1)=-v_0 \\[1em] \end{array} \right . \quad\quad\cdots\cdots\maru{4} \\[1em] \therefore \left\{\begin{array}{ll} & \kern -1em v_2=-v_0 \\[1em] & \kern -1em V_2=0 \end{array} \right . \] よって第2球は静止し,第1球は最初の衝突直前の速さで逆向きにはね返ることになり,一番最初の元の状態に戻ることになる。その後,はじめからの運動が繰り返される…というわけです。
☆計算方法について:
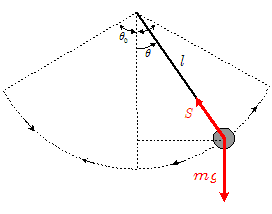
上図において,球にはたらく重力を$mg$,糸の長さを$l$とすると,小球の支点のまわりのモーメント$N$は \[ N=-mg\times l \times \sin \theta \] で与えられます。計算式として上式を使って解析したのが,「実際の運動に近い処理」です。この場合,その周期は(回転)角振幅$\theta_0$の大小によって変化します。(詳細は単振り子の運動を参照。)
これに対して「単振動として処理」では,\[N=-mg\times l \times\sin\theta \\ \kinji -mg\times l \times \theta \] という近似式を使って計算しています。この場合,小球の運動は単振動となり,その周期は角振幅$\theta_0$の大小に関係なく糸の長さ$l$と重力加速度$g$のみで決まってしまいます($\color{#ff00ff}{T=2\pi\kon{l/g}}$)。
小球の運動としては,その角振幅$\theta_0$が十分に小さいときにのみ単振動と近似できますが,回転角が大きくなってくると単振動としたのでは実際の運動とのズレが大きくなってしまいます。
先の「おまけ:2球の衝突」で述べた例は,2球の衝突が常に最下点で起こるという前提下でのみ成立します。このためには跳ね上がる高さに関係なく,2球が同じ時間間隔で最下点に戻ってこなくてはなりません。そのために「単振動」として処理する必要があったわけです。「実際の運動に近い処理」では落下時間が異なってくるので衝突する位置が毎回異なり,衝突する速度が衝突ごとにバラバラになり,再現性は見られなくなってしまいます。
単振り子の運動に関するシミュレーション,および詳細は以下をクリック。
単振り子の運動