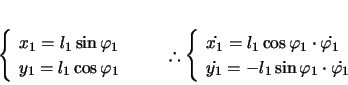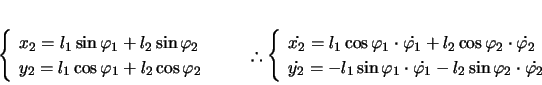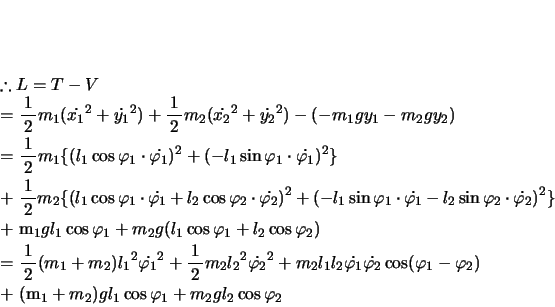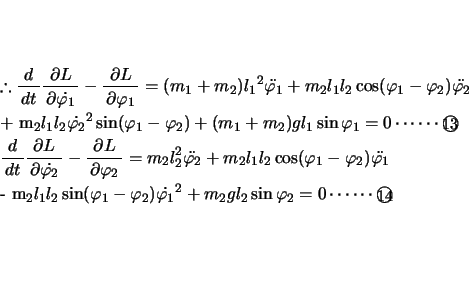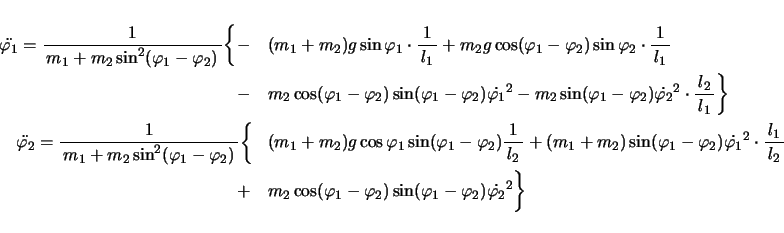2重振り子/単振動からカオスへ 詳解
戻る ビジュアル物理へ トップページへ
第1小球P(質量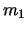 )が長さ
)が長さ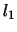 の針金aの下端につるされ,その下に第2小球Q(質量
の針金aの下端につるされ,その下に第2小球Q(質量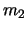 )が長さ
)が長さ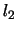 の針金bの下端に図のようにつるされているとする。針金aの上端は固定されており,ここを原点として,図のように座標軸を定める。2本の針金とも質量が無視できるが,曲がることはないとする。
の針金bの下端に図のようにつるされているとする。針金aの上端は固定されており,ここを原点として,図のように座標軸を定める。2本の針金とも質量が無視できるが,曲がることはないとする。
2本の針金が鉛直方向に対してなす角をそれぞれ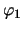 ,
,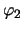 とし,針金の張力を
とし,針金の張力を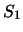 ,
,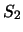 とすると,P,Qの水平方向,鉛直方向の運動方程式は,(
とすると,P,Qの水平方向,鉛直方向の運動方程式は,(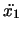 などの記号は
などの記号は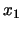 の時間の2階微分
の時間の2階微分
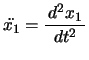 を意味する)
を意味する)
さらにP,Qが長さの決まっている針金に結ばれているとことを表す以下の式を加えて,P,Qの運動を知るための方程式がそろった。
ここでP,Qは十分に小さな振幅で運動しているとすると,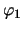 ,
,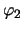 は十分に小さな量として近似をすると,
は十分に小さな量として近似をすると,
 より,
より,
上式を時間で2階微分して,
これを
 に代入し,さらに
に代入し,さらに
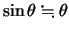 ,
,
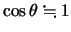 などの近似を適用すると,
などの近似を適用すると,
以上より,
 ,
,
 式は連立線形微分方程式で,この2式より
式は連立線形微分方程式で,この2式より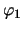 ,
,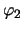 は二つの基準振動の合成として表すことができることが分かる(関連ページは、ここをクリック)。その基準振動数
は二つの基準振動の合成として表すことができることが分かる(関連ページは、ここをクリック)。その基準振動数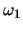 ,
,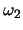 は,上記2式の連立より求められる。
は,上記2式の連立より求められる。
とくに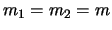 ,
,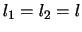 の場合は
の場合は
2つの基準振動数を求めるために,次の式変形をする(ただし,この方法は一般的なやり方ではない。一般的な方法は他を参照されたい。)。
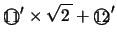 ,および
,および
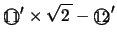 より
より
ここで
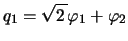 ,
,
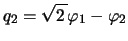 とおくと,上式は
とおくと,上式は
となり,これより基準振動数は,
と求まる。
であるから,もし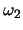 の振動が起きていなかったとすると
の振動が起きていなかったとすると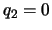 とおいて,
とおいて,
したがって,Pの変位が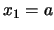 のとき,Qの変位は
のとき,Qの変位は
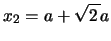 となる。つまり
となる。つまり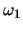 の基準振動は,2球の変位が常に同じ向きで,変位の大きさの比が
の基準振動は,2球の変位が常に同じ向きで,変位の大きさの比が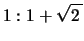 になった振動であることが分かる(図1)。
になった振動であることが分かる(図1)。
逆にもし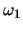 の振動が起きていなかったとすると,
の振動が起きていなかったとすると,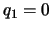 とおいて,
とおいて,
したがって,Pの変位が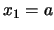 のとき,Qの変位は
のとき,Qの変位は
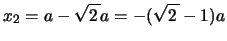 となる。つまり
となる。つまり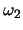 の基準振動は,2球の変位が常に逆向きで,変位の大きさの比が
の基準振動は,2球の変位が常に逆向きで,変位の大きさの比が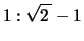 になった振動であることが分かる(図2)。
になった振動であることが分かる(図2)。
そして,P,Qの振動は,これら2つの基準振動を初期条件で決まる振幅比で組み合わせた運動となる。
振れ幅が大きいと、振り子の運動はカオスに・・・!
以上は,微小振動という条件の下で近似式が適用できた場合であった。しかしP,Qが大きく振れる場合はもちろん近似は使えず,厳密な解を求めていく必要がある。
この厳密解を求めるのに,これまでのやり方では計算が複雑になりすぎる。このような場合一般には,解析力学の立場から,Lagrangeの方程式を利用する。
これは,物体の運動エネルギー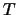 と位置エネルギー
と位置エネルギー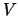 との差
との差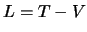 なる量
なる量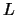 (Lagrange関数またはラグランジアンと呼ぶ)を位置座標成分と速度成分で表し,これを微分していくというやり方である。たとえば
(Lagrange関数またはラグランジアンと呼ぶ)を位置座標成分と速度成分で表し,これを微分していくというやり方である。たとえば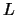 がある座標変数
がある座標変数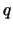 とおよびその時間微分量
とおよびその時間微分量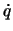 の関数であるとき,
の関数であるとき,
とおくことで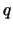 に関する運動方程式が得られるのである。
に関する運動方程式が得られるのである。
先の図のように,針金a,bが鉛直となす角度を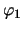 ,
,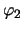 とすると,P,Qの座標は,
とすると,P,Qの座標は,
 ,
, 式を連立させて
式を連立させて
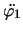 ,
,
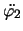 について解くと,
について解くと,
上式で得られる
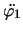 ,
,
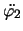 をもとに数値解析してシミュレーションしたのが先のアニメである。
をもとに数値解析してシミュレーションしたのが先のアニメである。
ここで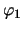 ,
,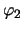 が十分に小さいとし,
が十分に小さいとし,
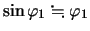 ,
,
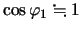 ,
,
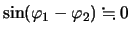 などの近似を行うと,先に連成振動として求めたのと同じ結果を得る。
などの近似を行うと,先に連成振動として求めたのと同じ結果を得る。
![\includegraphics[scale=1.1]{zyufuriko-kaisetu-1.eps}](img5.gif)
![\includegraphics[scale=1.1]{zyufuriko-kaisetu-1.eps}](img5.gif)
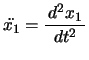 を意味する)
を意味する)
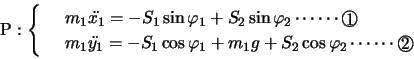
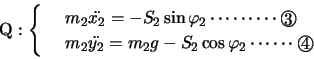
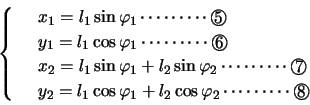
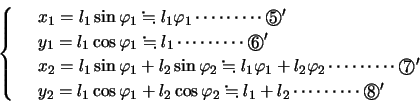
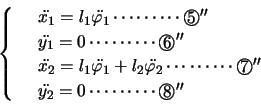
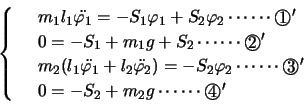
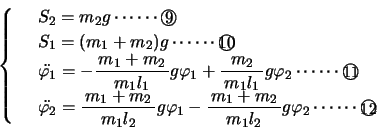
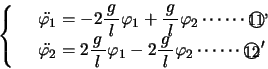
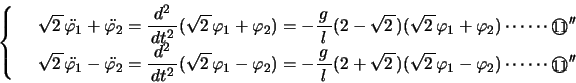
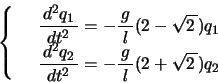
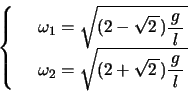
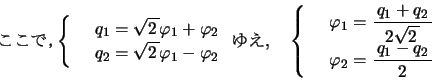
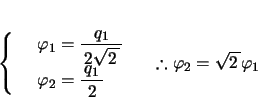
![\includegraphics[scale=1.1]{zyufuriko-kaisetu2-1.eps}](img48.gif)
![]() の振動が起きていなかったとすると,
の振動が起きていなかったとすると,![]() とおいて,
とおいて,
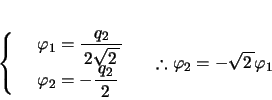
![]() と位置エネルギー
と位置エネルギー![]() との差
との差![]() なる量
なる量![]() (Lagrange関数またはラグランジアンと呼ぶ)を位置座標成分と速度成分で表し,これを微分していくというやり方である。たとえば
(Lagrange関数またはラグランジアンと呼ぶ)を位置座標成分と速度成分で表し,これを微分していくというやり方である。たとえば![]() がある座標変数
がある座標変数![]() とおよびその時間微分量
とおよびその時間微分量![]() の関数であるとき,
の関数であるとき,