2つ以上の振動子が相互に作用を及ぼしながら振動するとき,
 という。この場合,1つの振動子の運動は他の振動子の運動に影響を与え,逆にその振動子自身も他の振動子の影響を受ける。機械の振動,2つの音叉の共鳴など卑近な例をはじめとして,原子や分子といったミクロの世界にもこうした例はきわめて多い。
という。この場合,1つの振動子の運動は他の振動子の運動に影響を与え,逆にその振動子自身も他の振動子の影響を受ける。機械の振動,2つの音叉の共鳴など卑近な例をはじめとして,原子や分子といったミクロの世界にもこうした例はきわめて多い。
もっとも単純なモデルとして,2振子がばねに結ばれている例を考えよう。2つの振子P,Qはばね定数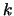 の2本のばねと,ばね定数の
の2本のばねと,ばね定数の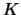 の1本のばねに結ばれ,
の1本のばねに結ばれ,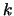 のばねは他端が固定され,
のばねは他端が固定され,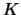 のばねはP,Q間に結ばれているとする。P,Qの質量はともに
のばねはP,Q間に結ばれているとする。P,Qの質量はともに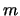 とする。
とする。
いまP,Qの平衡点からの変位が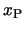 ,
,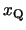 であるとき,それぞれの運動方程式は,
であるとき,それぞれの運動方程式は,
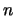 個の振動子からなる連成振動ではその運動方程式は
個の振動子からなる連成振動ではその運動方程式は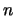 個の連立線形常微分方程式となり,その解は一般に
個の連立線形常微分方程式となり,その解は一般に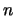 個の単振動の合成として表される。その単振動を
個の単振動の合成として表される。その単振動を
 ,またその振動数を基準振動数という。この場合は振動子2個ゆえ,2個の基準振動の合成となる。その基準振動数を求めるために,上記の運動方程式を以下のように書き直してみる。(この方法は、高校生にも理解できるようにしたもので、一般的ではありません。一般的な方法は、他を参照して下さい。)
,またその振動数を基準振動数という。この場合は振動子2個ゆえ,2個の基準振動の合成となる。その基準振動数を求めるために,上記の運動方程式を以下のように書き直してみる。(この方法は、高校生にも理解できるようにしたもので、一般的ではありません。一般的な方法は、他を参照して下さい。)
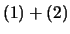 ,および
,および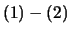 より,
より,
ここで,
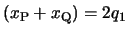 ,
,
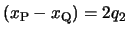 とおくと,
とおくと,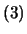 ,
,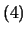 式は以下のようになり,これより2つの基準角振動数
式は以下のようになり,これより2つの基準角振動数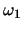 ,
,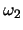 が求められる。
が求められる。
したがって,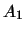 ,
,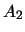 ,
,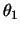 ,
,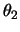 を初期条件より定まる積分定数として,
を初期条件より定まる積分定数として,
とおくと,
以上が、P、Qの時間変化を表す式である。定数部分は、初期条件によっていろいろ変わってくる。
たとえば一例として,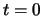 において
において
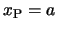 ,
,
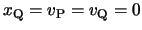 とすると,
とすると,
下の図1,図2は上記(10),(11)の場合で,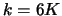 である場合の
である場合の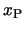 と
と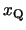 の時間変化を表している。これより分かるように,
の時間変化を表している。これより分かるように,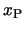 の振幅が最大の時刻と
の振幅が最大の時刻と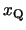 の振幅が最大となる時刻が交互になっていることが分かる。Pの振幅が減少するにつれてQの振幅が増大し,逆にQの振幅が減少するときPの振幅が増大していく。つまりPとQの間で振動エネルギーのやり取りが行われているわけです。これはPとQの固有振動数(この場合はP,Qの質量と両サイドのばねのばね定数で決まる)が等しいために起きる現象で,P,Qの固有振動数が異なる場合にはこのようなことは起きません。このことは先のシミュレーションでQの質量を1以外の値にしたとき,振幅の変化はきわめて起きにくいことから確認できるはずです。これが共振という現象です。
の振幅が最大となる時刻が交互になっていることが分かる。Pの振幅が減少するにつれてQの振幅が増大し,逆にQの振幅が減少するときPの振幅が増大していく。つまりPとQの間で振動エネルギーのやり取りが行われているわけです。これはPとQの固有振動数(この場合はP,Qの質量と両サイドのばねのばね定数で決まる)が等しいために起きる現象で,P,Qの固有振動数が異なる場合にはこのようなことは起きません。このことは先のシミュレーションでQの質量を1以外の値にしたとき,振幅の変化はきわめて起きにくいことから確認できるはずです。これが共振という現象です。
なお,もし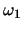 の振動しか起きていないとすれば,
の振動しか起きていないとすれば,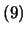 ,
,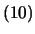 で
で とおくと
とおくと
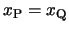 となり,PとQは常に同じ向きに同じ運動をすることになる。つまり,
となり,PとQは常に同じ向きに同じ運動をすることになる。つまり,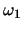 の振動
の振動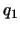 は下図3のような振動を表すことを意味する。また同様に,
は下図3のような振動を表すことを意味する。また同様に,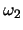 の振動しか起きていないとすれば,
の振動しか起きていないとすれば, ,
, で
で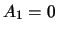 とおくと
とおくと
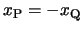 となり,PとQは常に逆向きの運動をすることになる。つまり,
となり,PとQは常に逆向きの運動をすることになる。つまり,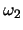 の振動
の振動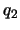 は下図4のような振動を表すことを意味する。
は下図4のような振動を表すことを意味する。
この場合のP,Qのような2振子の運動は,一般に下図3,4のような
 として表されることが知られている。
として表されることが知られている。
![\includegraphics [scale=.8]{kaisetu0-1.eps}](img1.gif)
![\includegraphics [scale=.8]{kaisetu0-1.eps}](img1.gif)
![]() の2本のばねと,ばね定数の
の2本のばねと,ばね定数の![]() の1本のばねに結ばれ,
の1本のばねに結ばれ,![]() のばねは他端が固定され,
のばねは他端が固定され,![]() のばねはP,Q間に結ばれているとする。P,Qの質量はともに
のばねはP,Q間に結ばれているとする。P,Qの質量はともに![]() とする。
とする。
![]() ,
,![]() であるとき,それぞれの運動方程式は,
であるとき,それぞれの運動方程式は,
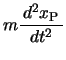
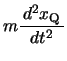
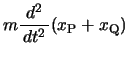
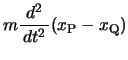
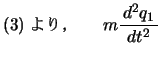
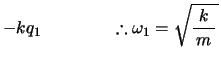
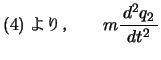
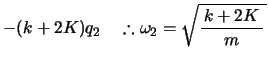
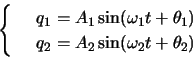
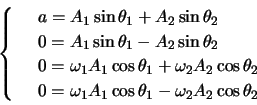
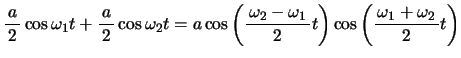
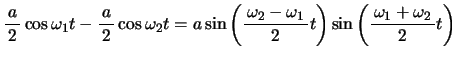
![\includegraphics[scale=.8]{kaisetu11-1.eps}](img49.gif)
![\includegraphics[scale=.8]{kaisetu12-1.eps}](img50.gif)
![]() の振動しか起きていないとすれば,
の振動しか起きていないとすれば,![]() ,
,![]() で
で![]() とおくと
とおくと
![]() となり,PとQは常に同じ向きに同じ運動をすることになる。つまり,
となり,PとQは常に同じ向きに同じ運動をすることになる。つまり,![]() の振動
の振動![]() は下図3のような振動を表すことを意味する。また同様に,
は下図3のような振動を表すことを意味する。また同様に,![]() の振動しか起きていないとすれば,
の振動しか起きていないとすれば,![]() ,
,![]() で
で![]() とおくと
とおくと
![]() となり,PとQは常に逆向きの運動をすることになる。つまり,
となり,PとQは常に逆向きの運動をすることになる。つまり,![]() の振動
の振動![]() は下図4のような振動を表すことを意味する。
は下図4のような振動を表すことを意味する。
![]() として表されることが知られている。
として表されることが知られている。
![\includegraphics[scale=.8]{kaisetu6-2.eps}](img62.gif)