オーディオ装置の目的は音楽信号を出来るだけ忠実に再生することにある。そのためには、再生周波数レンジが広く、歪が少ないことが必要となる。周波数特性に関しては、高域、低域それぞれ論じてきたが、歪みについては、高調波歪み、位相歪み、過渡歪などについて別項で断片的に取り上げている。ここでは、最も有害と考えられているアンプやスピーカーの非線形性に由来する歪みについて論じる。
内容は、非線形性とは、非線形性がもたらす高調波歪・混変調歪、歪んだ波形は？、非線形性の原因、歪と聴感、シミュレーションソフト
ここでいう非線形性とは、アンプの場合は入力電圧に対して、出力電圧(電流)が完全には比例していないことである。スピーカーの場合は、出力電圧の代わりに振動板の位置変化を考えればよい。
数式で示せば、入力電圧を ｘ、 出力電圧を ｙ とすれば、非線形性が無い場合は、y＝ ax であり、非線形性がある場合は
|
と表せる。第１項は線形、第２項は第１項と合わせると ｙ 軸に対し非対称な非線形性を、第３項は反対称（符号反転対称
）非線形性をもたらす。実際にはさらに高次の項まで存在するがここでは簡単のため省略する。具体的にその形を図に示すと、以下のようになる。
 |
図1-a 非対称非線形性 b > 0, c =0 実際にはA級作動の真空管アンプなどで生じる。 左サムネイルをクリックすると大きくなります |
 |
図1-ｂ 反対称非線形性 b=0, c >< 0 青線はｃ > 0 の場合（発散型） プッシュ・プルアンプなどで生じる 赤線は ｃ < 0 の場合（飽和型） 大振幅時にスピーカーで生じる。 左サムネイルをクリックすると大きくなります |
(1) 式で表せる非線形性が存在する時の出力波形は、単純コサイン波、混合コサイン波の波形
 |
 |
を（１）式に代入し、２倍角、3倍角の公式など、基本的な3角関数の公式を用いて変形すると、容易に導き出せる。ここで、ωは角振動数で、周波数を ｆ1、ｆ2 とすると、ω1＝2π*f1, ω2＝2π*ｆ2 で与えられる。
結果は、
 |
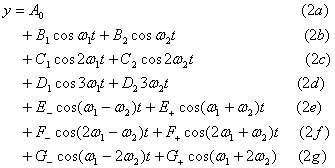となり、色々な周波数成分の重なった波となることがわかる。係数 A、B・・・G は少々煩わしいので別に書いておく。
ここでは、具体的に ｆ1＝110Hz, f2 = 510Hz, a=10, b=2, c=-2(飽和型反対称非線形） として計算した周波数成分の大きさを下に表にして示す。
| 高調波歪(%) A1=1, A2=0 |
混変調歪(%) A1=0.6, A2=0.4 |
||||||
| 係数 | 周波数 成分 |
周波数 | 非対称 b=2 c=0 |
反対称 b=0 c=-2 |
非対称 b=2 c=0 |
反対称 b=0 c=-2 |
|
| A0 | DC | 0 | 10 | 5.2 | 直流成分 | ||
| B1 | f1 | 110 | 10 | 10 | 6 | 5.4 | 入力波の増減 |
| B2 | f2 | 510 | 4 | 4.5 | |||
| C1 | 2f1 | 220 | 10 | 3.6 | 第２高調波 | ||
| C2 | 2f2 | 1020 | 1.6 | ||||
| D1 | 3f1 | 330 | 5 | -1.1 | 第３高調波 | ||
| D2 | 3f2 | 1530 | -0.3 | ||||
| E± | f1±f2 | 620 400 |
4.8 | 相互変調歪 （混変調歪） |
|||
| F± | 2f1±f2 | 730 510 |
4.3 | ||||
| G± | f1±2f2 | 1130 910 |
2.9 | ||||
非線形性があるときの歪み率
左表は、B1、B2 行を除いて、入力周波数成分に対する各高調波、混変調波の混入率（％）
B1、B2 行（空色欄）の数値は入力周波数成分の出力値。反対称非線形性がある時は、基本波の出力振幅が互いに影響しあって、一方の信号の出力値が他方の信号の振幅に影響されることを意味する。（下3-ｂ式） この現象を、狭い意味での『混変調』歪と呼び、nf1±mf2 成分は『相互変調』歪みと呼ぶことがある。
高次の非線形性による歪み
左表から高調波歪みは非対称項、即ち ｘ2 項からは2次（周波数 2ｆ ）の高調波が生じ、反対称項、即ち ｘ3 項からは3次（3f ）の高調波が生じることがわかる。同様に、ｘn 項からは ｎ次（nf）の高調波が生じる。
通常、非線形性に由来する歪みの大きさは、基本波（入力波）に対する高調波、相互変調波の割合（％）で表すが、実際どの様な波形をしているかを示しておく。なお、この波形歪みの様子は、周波数成分に分解しない方が直感的にはわかり易い。 例えば、飽和型の反対称非線形性（図1-ｂ赤線 大振幅時のスピーカーの場合など）がある場合、これにサイン波を入れた場合、大振幅になると振幅が押さえられるように変形することは容易に想像できる。具体的にスピーカーの場合大振幅信号が入ると、エッジが伸びきり、振幅が制限されることに相当する。
 クリックで拡大 |
単一入力 非対称非線形 b=2、c=0 第2高調波歪 A級真空管アンプの場合など。 上下（プラス側、マイナス側）で波形が異なることに注意。 なお、直流成分は差っ引いてある。 この様な波形は第2高調波が混ざることによって生じることもわかる |
 クリックで拡大 |
単一入力 発散型反対称非線形 b=0, c=2 第3高調波歪 B級プッシュプルアンプのクロスオーバー歪など。ただし、実際にはさらに大振幅になると飽和するので、(1)式に負の係数を持った奇数次項を付け加える必要がある。 ピーク値辺の波形が尖ってくる。第3高調波を正相で混ぜることにより生じていることがわかる。 |
 クリックで拡大 |
単一入力 飽和型反対称非線形 b=0, c=-2 第3高調波歪 スピーカーなど。 ピーク値辺りの波形が押さえられている。第3高調波を逆相で混ぜれことによって生じていることがわかる。 |
 クリックで拡大 |
2入力（A1=0.6, A2=0.4) 非対称非線形 b=2、c=0 混変調歪 プラス側出力のピークが尖り、マイナス側出力のピークが押さえられている。 |
 クリックで拡大 |
2入力（A1=0.6, A2=0.4) 非対称非線形 b=0、c=-2 混変調歪 プラス側マイナス側共、ピークが押さえられている。 スピーカーなどでは大振幅の低音信号が入って振動版が前（又は後ろ）に出きった辺りで高音信号が入ると出力が減少することに対応する。 |
アンプ
すでに、述べたようにアンプでは真空管やトランジスターなどの増幅素子に非線形性が存在する。トランジスターアンプの場合、普通プッシュプル方式のアンプなので反対称型の非線形性となる。設計の悪いB級アンプだといわゆるクロスオーバー歪により小振幅時に発散型の非線形性が生じる。しかし、プロの作ったアンプでは、このようなことが無いよう、AB級動作に近づけ,クロスオーバー歪を避けている。さらに、負帰還により歪は大幅に減少し通常高調波歪、混変調歪共 0.1％以下に抑えられている。しかし、負帰還を大きくかけ過ぎると、見掛けの歪率は減らすことは出来るが動作が不安定になるなど弊害もあるので歪率のカタログデータのみでアンプの良否を判断してはいけない。なお、真空管アンプは歪の原因となる出力トランスを使うこともあり、歪率は1桁大きい 1% 前後になるようである。
以上の、非線形性は増幅回路素子の非線形性によるものだが、コンデンサー容量の非線形性なども原因になりうるという話もある。しかし、最近のトランジスターアンプは殆んど信号回路に直接入るカップリングコンデンサーを使用しない直流アンプなので問題ない。また、大振幅低周波信号により電源電圧が揺さぶられ、高周波信号が変調する。即ち、混変調歪みが発生することが考えられる。これを押さえるには電源インピーダンスを下げることが基本になるが、最終段を別電源にするなど対策がとられている場合が多い。何れにせよ、アンプの電源の安定性は増幅回路とほぼ同等の重要性がある。一般にアンプは重い方がいいと言われるが、これは電源を充実しようとするとトランスを大きくしたり平滑コンデンサーの容量を大きくする必要があり、必然的に重くなるわけである。（ただし、いわゆるスイッチング電源を使っている場合はこの限りでない） この他、振動の影響など、アンプの混変調歪の原因について色々なことが言われているが、半導体アンプは振動に強く、本当に歪みの原因になるのかかなり疑問である。
スピーカー
スピーカーはいわば歪発生の巣である。大振幅時はエッジが延びきることによる飽和型反対称非線形、小振幅時は、振動板が前に出た場合と後ろへ下がった場合の復元力の違いによる非対称性、ギャップの磁束密度の不均一性からくる非線形性など数え上げればきりが無く、さらに、コーンの分割振動、過渡歪、ドップラー歪（低音信号に高音信号が重なった時後者がドップラー効果により変調される）、群遅延、ネットワークの位相歪などが重なり、オーディオシステムの中で最も歪発生源を抱えた不完全な代物である。その歪率だが、トランジスターアンプに比べて高調波歪は少なくとも1桁は大きいようである。オーディオシステムの音質の良否が殆んどスピーカーシステムで決定されるゆえんである。
歪があれば当然再生の忠実度を損なう。しかし、それが即音質の低下に結びつくかといえば必ずしもそうでない。良く知られているように、楽器の音色は、高さを決める基音とその高調波によって決まる。弦楽器や管楽器のように1次元発音源の場合、その高調波は基音の整数倍であり（太鼓やシンバルのような2次元発音体を持つものは異なる）、システムが発生する単純高調波はそれほど聴感を悪くしないといわれている。逆に、豊かな音色をもたらすことすらあるかもしれない。しかし、混変調歪（相互変調歪）はもともと楽音には含まれていない周波数成分なので音を汚す原因になると考えられているようである。
補 足 (2004.3.18 更新）
人間がどの程度の非線形歪を検知可能かについてのデータがあったので紹介しておく。（出典：田中茂良著『マイクロホン・スピーカ談義』 兼六舘出版 1995）
| 耳の良い5%の人が 検知できるレベル |
誰でも（90%の人）が 検知できるレベル |
||
| 音 声 |
偶数次高調波 | 6% | 14% |
| 奇数次高調波 | 1% | 3% | |
| 音 楽 |
偶数次高調波 | 3% | 10% |
| 奇数次高調波 | 1% | 6% | |
これを、見ると高調波歪については、１％以下に抑えてあれば十分であることが分かる。
残念ながら混変調歪についてのデータは見当たらなかった。ただ、上記の計算例でも分るように非線形性があれば、混変調歪みもほぼ同程度のレベルで発生するので相互変調歪のみを含む音源を作るのは難しく、上記の表はほぼ同程度の混変調歪み成分を含んでの結果と見て差し支えないであろう。
また、CCIR（国際無線通信諮問委員会）の高品質信号伝送線の満たすべき条件として以下の基準を勧告している（CCIR 1974年勧告）
| 特 性 | 周波数範囲(Hz) | 許容値 |
| f特 | 800または1000Hzを基準として | |
| 40 〜 125 | +0.5 〜 -2.0dB | |
| 125 〜 10000 | +0.5 〜 -0.5dB | |
| 1000 〜 14000 | +0.5 〜 -2.0dB | |
| 14000 〜 15000 | +0.5 〜 -3.0dB | |
| 群遅延時間 | 遅延時間の最小値との差が | |
| 40 | 55ms 以下 | |
| 75 | 24ms 以下 | |
| 14000 | 8ms 以下 | |
| 15000 | 12ms 以下 | |
| 雑音レベル | 実効値 | -47dB 以下 |
| 全高調波歪 | 40 〜 125 | 1％以下 |
| 125 〜 7500 | 0.5%以下 | |
| 第2、第3高調波歪 | 40 〜 125 | 0.7%以下 |
| 125 〜 7500 | 0.35%以下 | |
 |
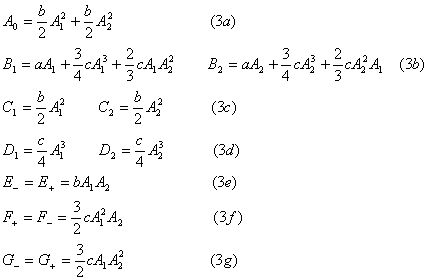Audio BBS に投稿されている◯町さんが作成された、各種歪みを生成するシミュレーションソフトのソースをアップロードしています。
Distortion.zip
ここを右クリックしてzip 圧縮ファイルを自分のパソコンの適当なフォルダーに保存して下さい。zip ファイルを解凍するとDistortion.exe
という実行ファイルが生成されます。
使用法等はここをクリックしてマニュアルを見て下さい。
不明な点は
に問い合わせていただければ作者に転送します。
あるいは直接Audio BBS に投稿してもらっても結構です。
なお、私自身では全ての機能をテストしたわけではありません。このソフトを使用することにより万一トラブルが生じても責任は負いかねます。自己責任で行って下さい。