正五角形の描き方は中学の技術の時間に習ったような気がするが,以来,コンパスと定規で作図することはついぞなく,すっかり忘れてしまっていた.しかし,ひょんなことから作図を思い立ち,ウェブで調べて,改めて作図の妙技に感心した.その感心ついでに,作図法を記録しておこうと思う.ウェブで調べたのだから,「屋上屋を架す」を地で行くことになるが.
†
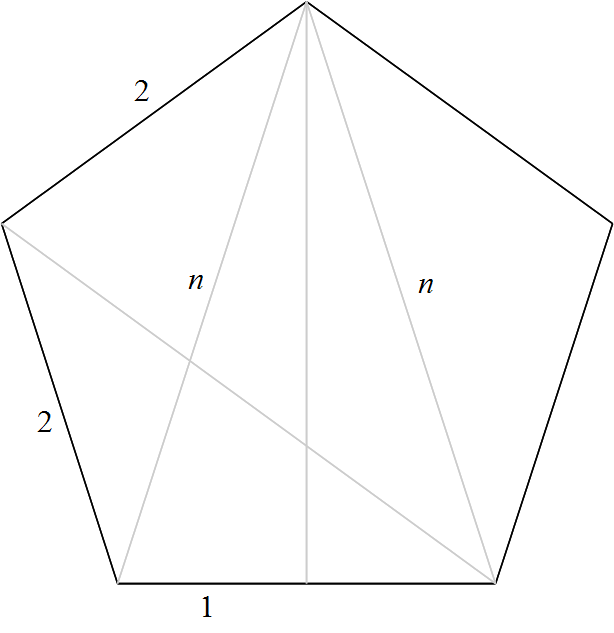
それでは,正五角形を描いてみよう.
さて,辺の長さがわかっているのだから,底辺に対向する頂点の位置がわかれば,残り2つの頂点はコンパスで求めることができる.底辺に対向する頂点が底辺の垂直二等分線上にあることは,対称性から明らかだ.したがって,底辺から頂点までの高さ,または対角線の長さを求めればよい.このうち,対角線の長さは,次のようにして計算することができる.
まず,正五角形を,「数学小辞典」(共立出版)に従い,
- 5つの辺の長さがすべて等しい
- 5つの内角の大きさがすべて等しい
定義から,正五角形の内角はすべて108°である.
ここでは,辺の長さを2とする.
*
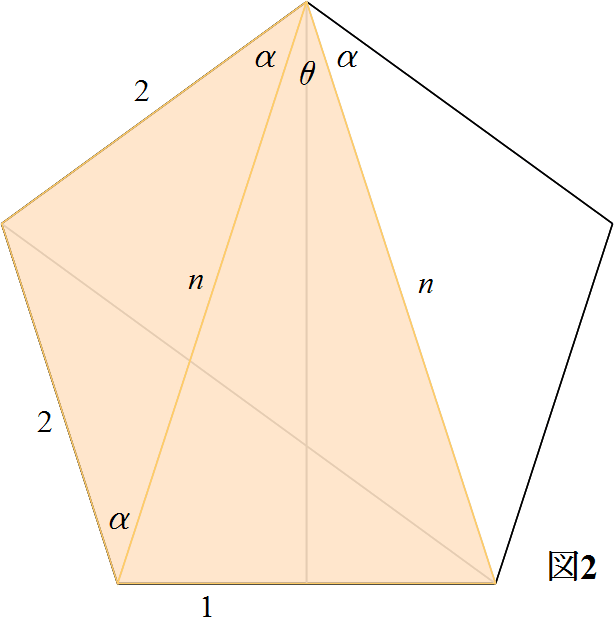
さて,2辺と対角線からできる二等辺三角形(図2の左側)は,定義から2辺狭角が等しく,すべて合同である.したがって,対角線の長さはすべて等しい.これをnとしよう.このnを求めるのが,ここでの課題である.
次に,この二等辺三角形の底角αは,頂角が正五角形の内角108°であることから,36°となる.また,1辺と2つの対角線からなる三角形(図の右側)は,対角線の長さがすべて等しいことから,二等辺三角形であり,その頂角θは
108°− 36°×2=36°
である.したがって,1辺と2つの対角線からなる二等辺三角形はすべて,2角狭辺が等しく,合同である.
*
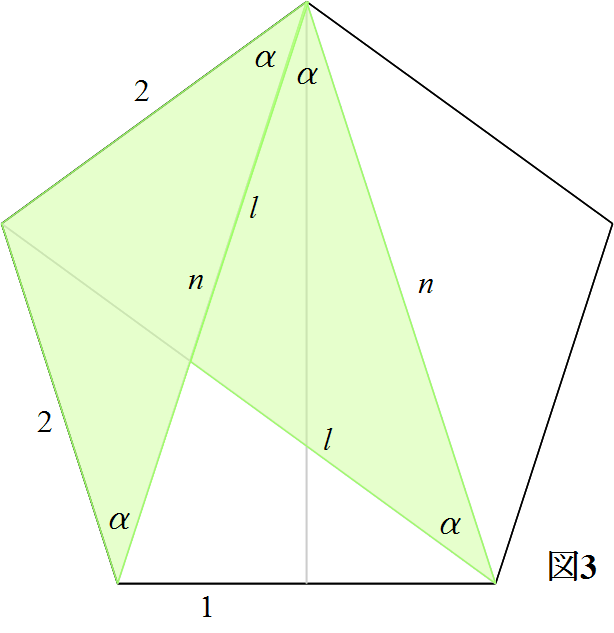
次に,図3の右側の三角形は,底角がいずれも1辺と2つの対角線からなる二等辺三角形の頂角であり等しいことから,二等辺三角形である.
そして,図3の2つの二等辺三角形は,底角と底辺の長さが等しく,合同である.
したがって,右側の三角形の2つの等辺の長さlは2である.
*

次に,図4の2つの三角形は,頂角と底角の一方(α)が等しいことから,相似である.
したがって,
n:2=2:(n−2)
が成り立つ.すなわち,
n(n-2)−4=0
n2−2n−4=0
したがって,
n=1+√5
となる.
*
以上で,対角線の長さがわかった.それでは,高さはどうかというと,三平方の定理から
√n2−1
√5+2√5
となるが,この長さは作図には向かないように思われる.そこで,対角線を用いて正五角形の作図に挑戦してみよう.底辺は与えられているものとする.ここで,2は底辺の長さ,1はその半分である.
*
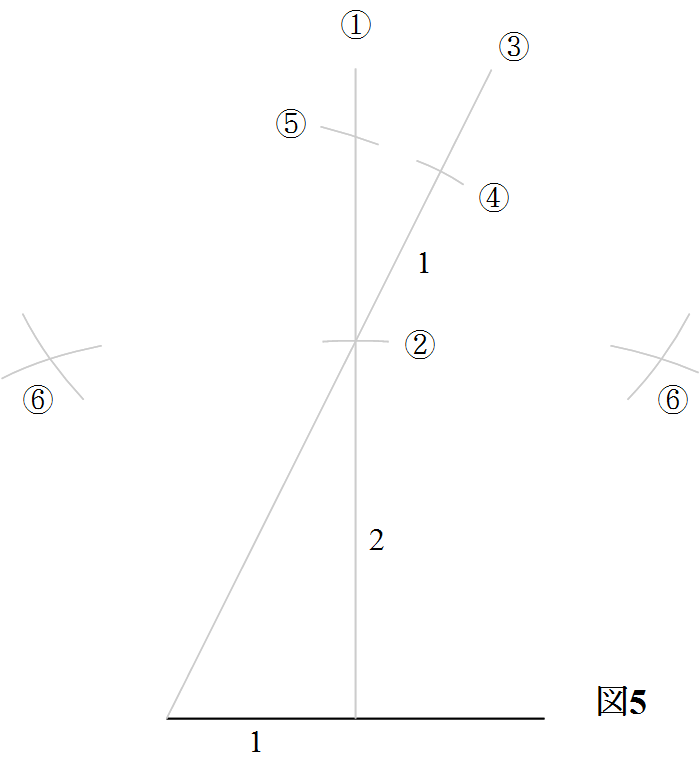
(1)底辺の中点から,垂線を引く.
(2)その垂線上で,底辺から2の距離にある点を求める.
(3)底辺の端点からその点を通る直線を引く.
(4)その直線と垂線との交点から1延長した点を求める.
底辺の端点からその点までの距離は1+√5である.
(5)垂線上で,底辺の端点からその距離にある点を求める.
その点が底辺に対向する頂点である.
(6)その頂点と底辺の2つの端点から,それぞれ2の距離にある点を求める.
その2つの点とすでに得ている3つの点を結べば,所与の底辺上に正五角形ができあがる.
*
こうして作図の手順をつぶさに観察すると,この手順の本質がコンパスと定規を使ってn2−2n−4=0という2次方程式を解くことにあることがわかる.
*
底辺が与えられたとき、正五角形を描く方法はわかった。ならば、円に内接する正五角形はどのようにすれば描けるだろうか。

辺の長さを簡単に求めることができればよいのだが、生憎、長さは二重根号で表現されるため、ちょっと厄介だ。
そこで、つらつら考えると、所与の底辺上に正五角形を描く際に出てきた底辺と対角線からできる二等辺三角形の頂角は36°、これは一周の10分の1だから内接正十角形を作る。そして底辺と斜辺の比は2:nと作図向きであることに気がつく。
ここでは、斜辺は円の半径であり、2:nは黄金比である。したがって、半径を黄金比に内分する点を求めれば正十角形の辺の長さが得られることになり、内接正十角形が描ければもちろん内接正五角形も描けることになる。
しかも、線分を黄金比に分ける点を求める作図法はすでに知られている。といっても、2に対して√5−1を作るだけのことだが。
ということで、次のようにして円に内接する正五角形を描くことができる。ここでは、円の半径を2とする。
*

(1)所与の円に、縦と横の直径を引く。
その縦の直径の下側半径を黄金比に内分しようというのである。
(2)縦の直径と円の交点から、横の直径の左側半径の中点に至る線分を引く。
この線分の長さは√5である。
(3)その線分から、半径の半分の長さを切り取る。
半径の半分の長さは1だから、残りの線分の長さは√5−1。すなわち、正十角形の辺の長さである。
(4)縦の直径と円の交点から、その長さを距離とする点を求める。
その2点が、内接正五角形の底辺の両端となる2つの頂点である。
(5)その頂点から、底辺の長さを距離とする点を求める。
これで、内接正五角形を構成する5つの頂点が得られた。
*
以上で、無事、円に内接する正五角形が描けた。