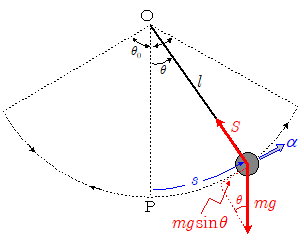
◎単振動としての近似
角振幅 $\theta_0$ が十分小さい場合,角 $\theta$ も小さいので,$\sin\theta \kinji \theta$ と近似でき,これより$\maru{2}$式は,\[ \bun{\mathrm{d}^2\theta}{\mathrm{d}t^2}=-\bun{g}{l}\times \sin\theta \kinji -\bun{g}{l}\times\theta \cdots\cdots\maru{3} \] ここで $\omega=\kon{\bun{g}{l}}$ とおけば,\[ \bun{\mathrm{d}^2\theta}{\mathrm{d}t^2}=-\omega^2\times \theta \cdots\cdots\maru{4} \]となり,角 $\theta$ は時間とともに単振動変化をすることになる(下記参照)。その周期 $T$ は,\[ T=\bun{2\pi}{\omega}=2\pi\kon{\bun{l}{g}} \]となる。よって周期 $T$ は振幅に関係なく,振り子の長さ $l$ と重力加速度 $g$ のみで決まることになる。このことを振り子の等時性 (振れ幅が大きくても小さくても周期が同じということ)という。
【参考】 $\maru{4}$ 式を満たす $\theta$ の解が単振動であることの確認:
$\theta_0$ を角振幅, $t$ を時間, $\delta$ を位相差として, $\theta=\theta_0\sin (\omega\, t+ \delta)$ とおくと,\[\quad \dif{\theta}{t}=\omega\cdot\theta_0 \cos (\omega\, t+\delta) \\ \therefore \ddif{\theta}{t}=\bun{\mathrm{d}}{\mathrm{d}t} \bigg( \dif{\theta}{t} \bigg)\\ \quad\quad\quad=\bun{\mathrm{d}}{\mathrm{d}t}\big(\omega\cdot\theta_0 \cos (\omega\, t+\delta)\big)\\ \quad\quad\quad=-\omega^2\cdot\theta_0 \,\sin (\omega\, t+\delta)\\ \quad\quad\quad=-\omega^2 \cdot\theta\]となり,$\theta=\theta_0\sin (\omega\, t+ \delta)$ は $\maru{4}$ 式を満たす。よって, $\theta$ は時間とともに単振動変化をすることがわかる。
◎ 円運動としての処理 - 周期は振幅に依存
これに対して角振幅 $\theta_0$ があまり小さくなく,$\sin\theta \kinji \theta$ という近似が適用できない場合,$\maru{2}$ 式のまま方程式を解かなければならない。この2階微分方程式から周期を求めることは容易ではない。
【参考】円運動としての振り子の周期:
周期を求めるには次のようにしていく。
角振幅を$\theta_0$とすると,振り子の最下点Pを位置エネルギーの基準点としたエネルギー保存則より,\[ 0+m\,g\,l\,(1-\cos\theta_0) = \bun{1}{2}mv^2+m\,g\,l\,(1-\cos\theta) \\ \therefore \bun{1}{2}mv^2=m\,g\,l\,(\cos\theta-\cos\theta_0)\] ここで $v=\dif{( l\,\theta)}{t}=l \dif{\theta}{t}$ であるから,上式は,\[\bun{1}{2}m\bigg(l\bun{\mathrm{d}\theta}{\mathrm{d}t}\bigg)^2=m\,g\,l\,(\cos\theta-\cos\theta_0) \\ \therefore \bun{\mathrm{d}\theta}{\mathrm{d}t}=\kon{\bun{2g}{l}}\kon{\cos\theta-\cos\theta_0}\\ \therefore \mathrm{d}t=\kon{\bun{l}{2g}}\bun{\mathrm{d}\theta}{\kon{\cos\theta-\cos\theta_0}} \] ここで運動の対称性から明らかなように,求める周期は $0 \le \theta \le \theta_0$ の運動の4倍になるので,\[ T=4\kon{\bun{l}{2g}}\int^{\theta_0}_0 \bun{\mathrm{d}\theta}{\kon{\cos\theta - \cos\theta_0}} \] 上式をさらに式変形していくと,第1種完全楕円積分とよばれる積分形になります。
(続きの詳しい計算はここをクリック)
この積分は解析的に初等関数としては表せませんが,パソコンなどによる数値解析で計算していくことはできます。下図にその計算結果を示します。
角振幅を$\theta_0$とすると,振り子の最下点Pを位置エネルギーの基準点としたエネルギー保存則より,\[ 0+m\,g\,l\,(1-\cos\theta_0) = \bun{1}{2}mv^2+m\,g\,l\,(1-\cos\theta) \\ \therefore \bun{1}{2}mv^2=m\,g\,l\,(\cos\theta-\cos\theta_0)\] ここで $v=\dif{( l\,\theta)}{t}=l \dif{\theta}{t}$ であるから,上式は,\[\bun{1}{2}m\bigg(l\bun{\mathrm{d}\theta}{\mathrm{d}t}\bigg)^2=m\,g\,l\,(\cos\theta-\cos\theta_0) \\ \therefore \bun{\mathrm{d}\theta}{\mathrm{d}t}=\kon{\bun{2g}{l}}\kon{\cos\theta-\cos\theta_0}\\ \therefore \mathrm{d}t=\kon{\bun{l}{2g}}\bun{\mathrm{d}\theta}{\kon{\cos\theta-\cos\theta_0}} \] ここで運動の対称性から明らかなように,求める周期は $0 \le \theta \le \theta_0$ の運動の4倍になるので,\[ T=4\kon{\bun{l}{2g}}\int^{\theta_0}_0 \bun{\mathrm{d}\theta}{\kon{\cos\theta - \cos\theta_0}} \] 上式をさらに式変形していくと,第1種完全楕円積分とよばれる積分形になります。
(続きの詳しい計算はここをクリック)
この積分は解析的に初等関数としては表せませんが,パソコンなどによる数値解析で計算していくことはできます。下図にその計算結果を示します。
この場合,周期は振れ角振幅に依存し,振れ角振幅が大きくなるほど周期は長くなる。
この様子を下図の青線に示す。横軸は振れ角振幅 $\theta_0$ を,縦軸は周期$T$が,単振動と見なせる時の周期 $T_0=2\pi\kon{\bun{l}{g}}$ の何倍になるか( $T/T_0$ )で示してある。赤線は振り子の運動が単振動であるとみなした場合の周期で,この場合はもちろん,その周期は角振幅の大小にかかわらず $T=T_0=2\pi\kon{\bun{l}{g}}$ である。
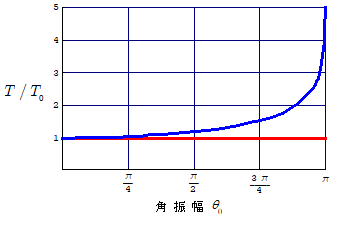
しかし振れ角振幅が $\pi$ に近づくと(糸ではなく,曲がらない軽い棒の先におもりを付けた振り子のような場合),周期は急激に増大していき,振れ角振幅 $\theta_0=\pi$ では周期は無限大となる。このとき振り子のおもりが支点の真上に来ていることになり,振り子の回転は起きないので,周期無限大となるのは当然である。
以上の値は数式(数学ソフトMathematicaのEllipticK関数を使用)から求めたものですが,本シミュレーションでも同様の結果が得られます。シミュレーションに戻って,初期角を設定し直して,再度確認してみてください。
(円運動としての周期計算の詳細は ここをクリック )