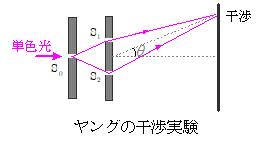
高校物理で学ぶ光の干渉実験として最も代表的なのがヤングの干渉実験です。この実験は上図のように,1つのスリット $\mathrm{S}_0$ に単色光を照射し,ここで回折した光が近接して置かれた2つのスリット(複スリット) $\mathrm{S}_1$ , $\mathrm{S}_2$ に入射して再度回折し,これが後方に置かれたスクリーン上で干渉して干渉縞をつくるというものです。
この実験では,物理的に2つの現象が起こっています。それは,波動の「干渉」であり,他の一つは「回折」です。
干渉は,複数の波が重なり合って強め合ったり弱め合ったりする現象で,回折は波が障害物にぶつかったとき,障害物の裏に波が回り込んで伝わっていく現象です。
この回折により,波が狭い隙間を通ると,波はいろいろな方向に広がっていきます。どの程度に回折が起きるかは,波の波長と隙間(スリット)の大きさの関係で決まります。
$\mathrm{S}_1$ , $\mathrm{S}_2$ で回折した光はさまざまな方向に広がり,さらにその回折光どうしが干渉を起こして干渉縞をつくるわけですが,このときできる干渉縞の強度分布(干渉縞の位置と明るさのとの関係)は,2つのスリット間の光路差のみならず,回折を左右するスリット幅の大きさ も関係してきます。結局全体として干渉縞の強度分布は,干渉による効果と回折による効果の相乗効果で決まることになります。
以下,干渉,回折について,やや詳しめの計算式を交えて考察していきましょう。
◎干渉による効果
まず,2つのスリット間の光路差と光強度分布 の関係について考えてみます。
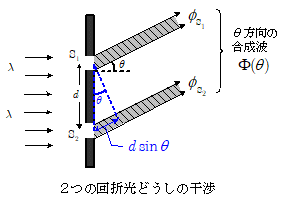
上図のように,スリット $\mathrm{S}_1$ , $\mathrm{S}_2$ の間隔を $d$ とします。
この2つのスリットに波長 $\lambda$ の光が入射したとしましょう。
光波の振動数を $\nu$ ,スリット$\mathrm{S_1}$ ,$\mathrm{S_2}$ を通って角 $\theta$ の方向に回折した光波の振幅を$A(\theta)$ とします。$A(\theta)$ は回折によって決まる値であり(詳細は 後述),$A(\theta)$ は回折角 $\theta$ とスリット幅のみの関数であって,スリット間隔 $d$ を含まない値であることに留意しておいてください。
いま,スリット $\mathrm{S}_1$ を通って角 $\theta$ 方向に回折した光波 $\phi_\mathrm{S_1}$ が\[\phi_\mathrm{S_1}=A(\theta)\sin2\pi\nu t \]と表されるとします。
この2つのスリット間の光路差 $\varDelta _\mathrm{S_1S_2}$ は,上図よりわかるように,$\varDelta _\mathrm{S_1S_2}=d\sin\theta$ となりますので,$\mathrm{S_2}$ を通った光波 $\phi_\mathrm{S_2}$ は$\mathrm{S_1}$を通った光波 $\phi_\mathrm{S_1}$ より光路差 $\varDelta _\mathrm{S_1S_2}$ を伝わる分だけ位相が遅れることを考慮して,\[ \phi_\mathrm{S_2}=A(\theta)\sin 2\pi\bigg(\nu t-\bun{d\sin\theta}{\lambda}\bigg) \]と表されます。ただしここではスリット自身の幅はスリット間隔 $d$ に比べて十分に小さく,現段階では,各スリット内での光線の位相差は考えないこととします。
上記の光波が重なって後方に置かれたスクリーン上で干渉を起こすわけですが,その合成波を $\varPhi(\theta)$ とすると, $\varPhi(\theta)$ は,\[\sin\alpha + \sin\beta = 2\cos\bun{\alpha-\beta}{2}\cdot \sin\bun{\alpha+\beta}{2} \]の公式を利用して,\[\varPhi(\theta)=\phi_\mathrm{S_1}+\phi_\mathrm{S_2}\\\quad=A(\theta)\bigg\{\sin2\pi \nu t+\sin2\pi\bigg(\nu t -\bun{d\sin\theta}{\lambda}\bigg)\bigg\} \\\quad =2A(\theta)\cos\bigg(\bun{\backslash \kern-0.5em 2 \pi \, d\,\sin\theta}{\backslash \kern-0.5em 2\lambda}\bigg)\cdot \sin2\pi\bigg(\nu t-\bun{d\sin\theta}{2\lambda}\bigg) \]となります。
上式右辺第2項は時間 $t$ を含んでおり,合成波 $\varPhi(\theta)$ が振動数 $\nu$ で振動していることを意味しています。そして上式右辺第1項の絶対値が,この振動の振幅を表すことになります。\[\therefore 合成波の振幅 \: C(\theta)=2\bigg|A(\theta)\cos\bigg(\bun{\pi}{\lambda}d\sin\theta\bigg)\bigg| \] 光の強さは振幅の2乗に比例( 参考)するので, $\theta$ 方向に進む合成光波 $\varPhi(\theta)$ の強度を $I(\theta)$ ,$\theta=0$ 方向に進む合成光波(直進光) $\varPhi(0)$ の強度を $I(0)$ とすると,\[\quad I(\theta)\:\propto \: C(\theta)^2 \\ \quad I(0)\:\propto \: C(0)^2 \\\therefore \bun{I(\theta)}{I(0)}=\bigg \{ \bun{C(\theta)}{C(0)}\bigg \}^2\\\quad\quad\quad\quad =\bigg\{\bun{\backslash \kern-0.5em 2 A(\theta)}{\backslash \kern-0.5em2 A(0)} \times \bun{\cos\bigg(\bun{\pi}{\lambda}d\sin\theta\bigg)} {\cos\bigg(\bun{\pi}{\lambda}d\sin (0)\bigg)}\bigg\}^2 \\\quad\quad\quad\quad =\bigg\{\bun{A(\theta)}{A(0)} \times \bun{\cos\bigg(\bun{\pi}{\lambda}d\sin\theta\bigg)}{1}\bigg\}^2\\ \quad\quad\quad\quad =\bigg\{ \bun{A(\theta)}{A(0)} \bigg\}^2 \times \cos^2\bigg(\bun{\pi}{\lambda}d\sin\theta\bigg) \] よって\[ \left \{ \begin{array}{rl} & \kern-1em f(\theta)=\bigg \{ \bun{A(\theta)}{A(0)}\bigg\}^2 \cdots\cdots\maru{1} \\ & \kern-1em g(\theta)=\cos^2\bigg(\bun{\pi}{\lambda}d\sin\theta\bigg) \cdots\cdots\maru{2} \end{array} \right . \] とおくと,上式は, \[\bun{I(\theta)}{I(0)}= f(\theta)\times g(\theta) \cdots\cdots\maru{3} \]となります。
ここで, $A(\theta)$ はスリットの間隔 $d$を含まない関数としていますので,$\maru{1}$ 式で表される $f(\theta)$ もスリット間隔 $d$ によらない関数であることになります。一方 $g(\theta)$ は,$\maru{2}$ 式 より,スリット間隔 $d$ を含みます。したがって,2スリット間の光路差 $d\sin\theta$ が光強度にどのように影響しているか,すなわち2スリットの回折光どうしの干渉の効果を調べるには $g(\theta)$ のみの性質を調べればよいことになります。
ここで,$g(\theta)=\cos^2\bigg(\bun{\pi}{\lambda}d\sin\theta\bigg)$ と $d \sin\theta$ の関係をグラフに描くと,およそ下図のようになります。
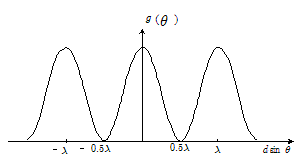
$\maru{2}$ 式(および上図)より,干渉による効果としての光の強度と回折角 $\theta$ の関係として以下のことが分かります。すなわち,
\[\kern-1em \varDelta _\mathrm{S_1S_2}=d\sin\theta = \left \{ \begin{array}{rl} & \kern-1em m\lambda のとき g(\theta)=1\quad\therefore I(\theta)= 極大 \quad \rightarrow 明線 \\ & \kern-1em \bigg(m+\bun{1}{2}\bigg)\lambda のとき g(\theta)=0 \quad\therefore I(\theta)=0 \quad \rightarrow 暗線 \end{array} \right . \quad\cdots\cdots\maru{4} \] ただし,$\quad\quad m=0,\pm1,\pm2,\pm3,\cdots\:,|m| < d/\lambda $
上記の関係は $f(\theta)$ の如何にかかわらず言えることであり,これが2スリット型干渉計の干渉条件ということになります。
次へ(回折による効果) 次の次へ(全体としての光強度)